Induktion, also die Erzeugung einer elektrischen Induktionsspannung, ist über verschiedene Wege möglich.
In diesem Artikel zeigen wir die bisherigen Erkenntnisse auf und vervollständigen das physikalische Phänomen der Elektromangnetischen Induktion um eine weitere Möglichkeit eine Induktionsspannung zu erzeugen.
Viel Spaß dabei!

Wiederholung
Bewegen wir einen elektrischen Leiter der (wirksamen) Länge mit der Geschwindigkeit (Weg pro Zeit ) in ein magnetisches Feld wird mittels Ladungsträgertrennung durch die Kraft eine Induktionsspannung am Leiterstück erzeugt. Nach gleichem Prinzip funktioniert dies mit einer Leiterschleife der Flächenausdehnung .
Zur Wiederholung empfehlen wir den Artikel siehe LINK Elektromagnetische Induktion Teil 1
Drehen wir eine Leiterschleife (mit ihrer Flächenausdehnung ) in einem magnetischen Feld , ändert sich die im Magnetischen Feld wirksame Fläche (Flächenanteil jeweils zu ) über die Zeit. Der sich damit im Magnetfeld ändernde Quotient erzeugt eine sinusförmige Induktionsspannung abhängig vom jeweiligen Drehwinkel .
Zur Wiederholung empfehlen wir den Artikel siehe LINK Elektromagnetische Induktion Teil 2
Betrachten wir die aufgezeigten Formeln, so fällt auf, das bislang nur ein Größe als konstant angesehen wurde, jene der Magnetischen Flußdichte . Sofern nicht, erzeugt auch ein sich änderndes Magnetfeld eine Induktionsspannung , was wir nachfolgend näher betrachten werden.
Induktion durch Änderung der Magnetischen Flußdichte B
Analog zur bislang genutzten Formel zur Berechnung der Induktionsspannung durch Änderung der Fläche (ausgedrückt mit Quotient ) gilt diese entsprechend angepasst auch für Änderungen der Flußdichte , letzteres wir durch einen Quotienten ausdrücken können:
Es gilt vereinfachend:
Die Fläche Leiterschleife , da
Definition: Eine Spule (ist eine Vielzahl von Leiterschleifen der Fläche somit)
"-" (Minus) steht für das Lenz’sches Gesetz (dazu später mehr)
Lenz’sches Gesetz, ganz einfach!
In obiger Formel bringt das "Minus" das Lenz’sches Gesetz zum Ausdruck, welches besagt, dass die Induktionsspannung immer ihrer Ursache entgegenwirkt. Was heißt dies konkret?
Steigt die magnetische Flußdichte in Form des Quotienten an (ist dieser also positiv), wird eine negative Induktionsspannung erzeugt, wirkt also ihrer Ursache entgegen.
Fällt oder sinkt die magnetische Flußdichte in Form des Quotienten ab (ist dieser also negativ), wird eine positive Induktionsspannung erzeugt.
Praktische Anwendung - Der Transformator
Was nützt all die umfangreiche Theorie, wenn wir diese nicht an einem praktischen Beispiel anwenden könnten. In der Elektrotechnik gibt es ein zentrales wie wichtiges Bauelement, ohne dieses viele uns bekannte elektrotechnische Geräte nicht genutzt werden könnten.
In nachfolgender Abb. 1 ist ein Transformator (in Kurzform auch Trafo genannt) dargestellt:
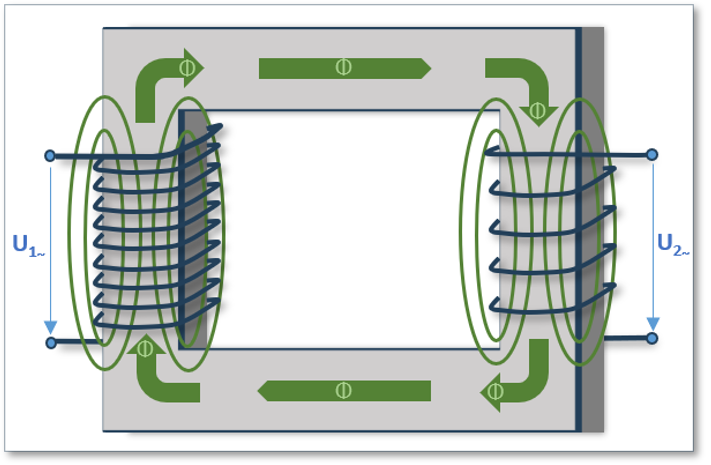
Abb. 1: Schematische Darstellung eines Transformators mit Magnetischem Fluss
Wozu wird ein Transformator gebraucht und benutzt?
Im Grunde genommen hat ein Transformater zwei Hauptaufgaben, indem er . . .
Zwei Stromkreise (Primär- und Sekundärstromkreis) galvanisch voneinander trennt. Hierbei ist gemeint, dass zwei Stromkreise nicht direkt elektrisch miteinander verbunden, sondern elektrisch entkoppelt sind. Die Kopplung findet ausschließlich über das Magnetische Feld statt.
Ein Spannungsniveau (im Primärstromkreis) auf ein anders Spannungsniveau (im Sekundärstromkreis) absenkt oder anhebt. Gleichermaßen kann die jeweilige Höhe der Stromstärke in den beteiligten Stromkreisen umgewandelt also transformiert werden.
Unser Transformator in Abb. 1 würde beispielsweise (aufgrund der Anzahl der Wicklungen der beiden Spulen) eine eingehende Wechselspannung am Ausgang mit halbieren.
In der alltäglichen Anwendung im Haushalt finden wir unzählige verbaute Transformatoren (Abb. 2), um (sogeannnte Niedervolt-) Geräte wie Halogenlampen, Computer, Lichterketten, Fernseher, Türklingel, Haushaltsmaschinen, u.v.m., an der üblichen Haushaltsspannung von 230V nutzen zu können. In Bereichen der Stromerzeugung und Verteilung, ebenso der Industrie, gibt es unzählige Anwendungen auf welche wir an dieser Stelle zunächst nicht eingehen können.
Abb. 2: Exemplarische Spannungsumwandlung im Bereich des Haushalts
Die Namensgebung TRANSFORMATOR kommt übrigens aus dem lateinischen "transformare", was soviel heißt wie umgestalten oder verwandeln.
Wie ist ein Transformator aufgebaut?
Zum prinzipiellen Aufbau:
Mit isoliertem Draht werden 2 Spulen um einen magnetisch leitfähigen z.B. Ringkern (Material , LINK) gewickelt.
Die beiden Spulen (mit jeweiliger Wicklungszahl , ) sind wegen des isolierten Drahtes nicht elektrisch miteinander verbunden.
. . . ist nur mit Änderung des Magnetischen Flußes und damit mit der Änderung der Magnetischen Flußdichte möglich!
Herzlichen Glückwunsch!
Wir haben das einführende Ende dieses spannenden Themas und somit auch das Ende dieses Artikels erreicht!

Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
Artikel
Quellen
- https://pixabay.com
- Bilder in Eigenkonstruktion
