Elektromagnetismus - Der Transformator

Ein universelle Zaubermaschine?

Im Kern stellt ein Transformator ein derartiges allerdings elektrotechnisches Bauelement dar.

Allerdings weniger von Zauberhand, kann stattdessen mittels elektromagnetischer Induktion eine Eingangsgröße verändert (konkret verringert oder erhöht) werden, wobei ein Transformator zudem in beiden Richtungen funktioniert.

Neugierig geworden?

Abb. 1: Symbolbild

Einführung und Wiederholung

Zum besseren und einfacheren Verständnis der nachfolgenden Inhalte empfehlen wir Dir die Wiederholung eines einführenden Artikels siehe LINK $\to$ Elektromagnetische Induktion - Teil 3

Wir haben uns im einführenden o.g. Artikel demnach zunächst über den grundsätzlichen Nutzen, den Aufbau und der Funktionsweise von Transformatoren ganz allgemein befasst.

Im Weiteren werden wir uns in diesem Artikel um die transformierten Größen und deren formale Zusammenhänge bemühen. Schließlich müssen derartige Transformatoren richtig dimensioniert, gebaut und für den jeweiligen Einsatz passgenau eingesetzt werden können.

Formale Zusammenhänge

Wie schon in Abb. 3 ersichtlich, sind selbstverständlich die beteiligten Spannungen, die eingespeiste Primärspannung $U_{1}$ sowie die erzeugte Sekundärspannung $U_{2}$ von zentralem Interesse.

Wird eine elektrische (Wechsel) Spannung an die Primärspule mit der Windungszahl $N_{1}$ angelegt, fließt selbstverständlich auch ein elektrischer Strom $I_{1}$ . Wird dadurch in der Sekundärspule mit der Windungszahl $N_{2}$ eine (Wechsel) Spannung induziert, fließt selbstverständlich auch hier ein elektrischer Strom $I_{2}$ . All diese Größen sind nun in unserem Beispiel-Transformator in Abb. 4 eingezeichnet.

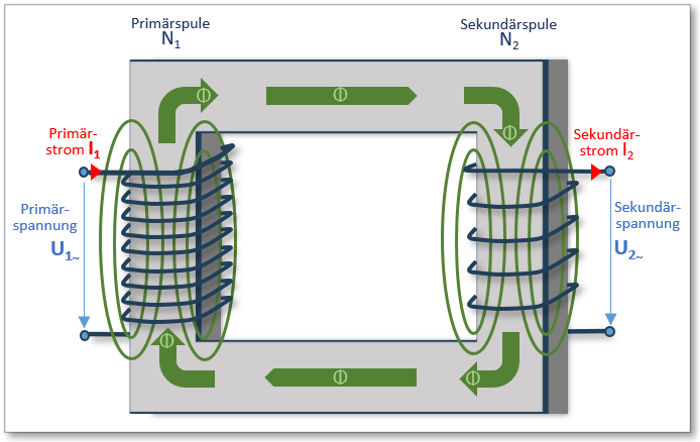
Abb. 4: Schematische Darstellung eines Transformators inkl. aller Primär- und Sekundärgrößen — **Abb. 4:** Schematische Darstellung eines Transformators inkl. aller Primär- und Sekundärgrößen

1) Der ideale Transformator

a) Spannungsübertragung bei einem $i d e a l e n, u n b e l a s t e t e n$ Transformator

Zwischen dem Verhältnis von Sekundär- und Primärspannung $\frac{U_{2}}{U_{1}} = \frac{U_{S}}{U_{P}}$ sowie dem Verhältnis der Windungszahlen von Sekundär- und Primärspule $\frac{N_{2}}{N_{1}}$ besteht folgender Zusammenhang:

Merke

$\frac{U_{2}}{U_{1}} = \frac{U_{S}}{U_{P}} = \frac{N_{2}}{N_{1}}$

Die Primärspannung $U_{1}$ (oder $U_{P}$ ) bestimmt hierbei die Sekundärspannung $U_{2}$ (oder $U_{S}$ )

b) Stromübertragung bei einem $i d e a l e n, b e l a s t e t e n$ Transformator

Zwischen dem Verhältnis von Sekundär- und Primärstrom $\frac{I_{2}}{I_{1}} = \frac{I_{S}}{I_{P}}$ sowie dem Verhältnis der Windungszahlen von Primär- und Sekundärspule $\frac{N_{1}}{N_{2}}$ besteht folgender Zusammenhang:

Merke

$\frac{I_{2}}{I_{1}} = \frac{I_{S}}{I_{P}} = \frac{N_{1}}{N_{2}}$

Der Sekundärstrom $I_{2}$ (oder $I_{S}$ ) bestimmt hierbei die Primärstrom $I_{1}$ (oder $I_{P}$ )

2) Der reale Transformator

Im Unterschied zum idealen Transformator treten beim realen Pendant demnach Verluste auf. Zu deren Bewertung wird die am Transformator abgegebene Leistung $P_{S}$ in das Verhältnis zur eingespeisten Leistung $P_{P}$ gesetzt. (Zur Erinnerung: $P = U \cdot I$ )

Dieses Verhältnis, genauer den Quotienten, hat man sogleich als den Wirkungsgrad $η$ definiert. $η$ (für Eta) ist demnach eine dimensionslose Größe, welche auch in Prozent angegeben wird.

MerkeDer Wirkungsgrad $η$ eines Transformators

$η = \frac{P_{S}}{P_{P}} = \frac{U_{S} \cdot I_{S}}{U_{P} \cdot I_{P}}$

Es ist definiert:

$η =$ 1 (bzw. $=$ 100%): Idealer Transformator ohne Verluste

$η <$ 1 (bzw. $<$ 100%): Realer Transformator mit Verlusten

Umso kleiner demnach der Wirkungsgrad $η$ , umso größer die Verluste im Transformator!

Du hast es geschafft! Weiter mit einer Übungsaufgabe?

Übungsaufgaben

Laden

Quellen

https://pixabay.com
Bilder in Eigenkonstruktion

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?