Das Hexadezimalsystem wird in der Datenverarbeitung genutzt. Prinzipiell ist die Grundlage unseres digitalen Umfeldes die Verarbeitung der Ziffern 0 und 1 (Binärsystem). Im Hexadezimalsystem kann man Informationen, die im Binärsystem 8 Stellen brauchen, komfortabel mit nur 2 Stellen darzustellen.
Definition
„Hexadezimal“ (von griech. hexa „sechs“ und lat. decem „zehn“) ist ein lateinisch-griechisches Mischwort. Das Hexadezimalsystem ist also ein Stellenwertsystem zur Basis 16. Man braucht also 16 Ziffern, um Zahlen im Hexadezimalsystem darzustellen. Dies sind die Ziffern 0, 1 bis 9 und die Buchstaben A, B, C, D, E und F. [1]
Wobei R für die Basis (hier 16) und Z für die Menge seiner Ziffern steht.
Darstellung
Zur Darstellung einer Zahl im Hexadezimalsystem werden die Ziffern wie auch im Dezimalsystem ohne Trennzeichen hintereinander geschrieben. Ihr Stellenwert entspricht der zur Stelle passenden Sechszehnerpotenz. Die höchstwertige Stelle wird ganz links und die niederwertigeren Stellen in absteigender Reihenfolge rechts davon aufgeschrieben.
Dezimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Hexadez. | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
Umrechnung in das Dezimalsystem
Auch das Hexadezimalsystem ist - wie das Dezimalsystem - ein Stellenwertsystem. Daher kann man von einer gegebenen Hexadezimalzahl auf die gleiche Weise den Gesamtwert als Dezimalzahl ermitteln. Das heißt, jede Stelle der Zahl hat eine bestimmte Wertigkeit. Wenn man die Stellen nun durchnummeriert und bei den Einern mit 0 beginnt, kann man die Wertigkeit der einzelnen Stellen wie folgt zur Basis 16 ausdrücken:
| |
|---|---|
|
|
|
|
|
|
|
|
Beispiel: Umrechnung Hexadezimalzahl: FF in Dezimal
Addiert man nun die einzelnen Potenzwerte der Stellen, bekommt man den Gesamtwert der Hezadezimalzahl: FF als Dezimalzahl:
Umrechnung in andere Stellenwert-Systeme
Die Umrechnung zwischen Binärsystem und Hexadezimalsystem ist relativ einfach, da die Zahl 16 selbst eine Zweierpotenz ist ( ). Das bedeutet, je vier Ziffern im Binärsystem entsprechen einer Ziffer im Hexadezimalsystem.
Anwendungen
Wie bereits zu Beginn dieses Artikels kurz bemerkt, werden Zahlen aus dem Hexadezimalsystem überwiegend in der Informatik verwendet. Die oft sehr großen Binärzahlen können somit im Hexadezimalsystem relativ komfortabel dargestellt werden. Ein sichtbarer Beweis dieser Feststellung ist die Farbcodierung in HTML in vielen unserer Web-Pages.
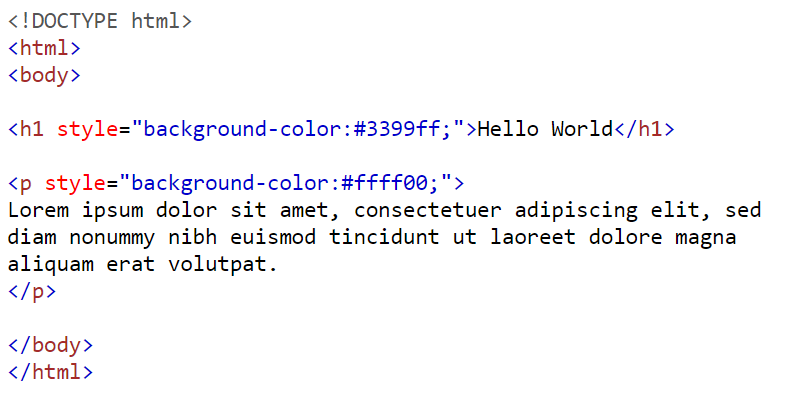
Dieses kurze HTML Snippet zeigt eine kleine Web-Page mit einer Überschrift "Hello World" und einem blauen Hintergrund, sowie einen Lorem ipsum Text Snippet auf gelbem Hintergrund.

Dabei steht die Hexadezimalzahl für:
# Farbcode des Hintergrundes der Überschrift
# Farbcode des Hintergrundes des Kapitels
Der Farbcode ist aus drei einzelnen Hexadezimalzahlen zusammengesetzt, hier als Beispiel die Codierung des Hintergrundes der Überschrift:
die für die Farbzusammensetzung des RGB Signals stehen.
Dabei werden die Farben in einem additiven Farbraum basierend auf den drei Grundfarben (Rot, Grün und Blau) erzeugt. Werden die drei Grundfarben in geeigneter Helligkeit addiert, entsteht die Farbempfindung Weiß. Schwarz entsteht, wenn die Summe Null ist.[2] Wie im Bild zu erkennen ist, ergeben die Addition von Rot und Grün (der ersten beiden der 3 Grundfarben) Gelb, wie auch der Hintergrund in unserem HTML Beispiel.

Wenn man also die drei Grundfarben addiert:
so entsteht Weiss als Ergebnis.

Setzt man jedoch die drei Grundfarben auf Null:
so entsteht Schwarz als Ergebnis.

Übungsaufgabe:
Mit welchen Hexadezimalcode kann man die Farbe Rot codieren. Für die Lösung bitte an die Grundfarben des additiven Farbraumes denken, welche Farben waren das noch einmal und an welcher Stelle steht welche Farbe ?
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
Artikel
- Zahlensysteme
- Stellenwertsysteme
- Dezimalsystem
- Oktalsystem
- Binärsystem
- Additionssysteme
- Hybridsysteme
- Römische Zahlen
