Wenn man verstehen will wie Computer mit Daten umgehen, muss man das Binärsystem verstehen. Aber keine Sorge - es funktioniert eigentlich ganz ähnlich wie das Dezimalsystem, das man aus der Grundschule kennt.
Definition
Das Binärsystem, auch Zweiersystem oder Dualsystem genannt, ist ein Zahlensystem, das zur Darstellung von Zahlen nur zwei verschiedene Ziffern benutzt [1]. Es ist ein Stellenwert-Zahlensystem zur Basis 2. Somit muss dieses Zahlensystem mit 2 Ziffern, nämlich der 0 und 1 auskommen. Diese Ziffern haben den gleichen Wert wie im Dezimalsystem.
Wobei R für die Basis (hier 2) und Z für die Menge seiner Ziffern steht.
Mit diesen beiden Ziffern kann man auch hervorragend technische Zustände beschreiben, wie
Schalter (offen / geschlossen)
Spannung (0V / > 0V)
Laser (kein Licht / Licht)
Somit ist das Binärsystem Grundlage der Funktionsweise alle unserer Computer. Der Grund ist ganz einfach. Computer arbeiten mit Bits und deren Zustand lässt sich praktisch mit 2 physikalische Zuständen beschreiben. Entweder es fließt Strom oder es fließt kein Strom. Anders ausgedrückt kann ein Computer nur die beiden Zustände ON und OFF erkennen.
Darstellung
Zur Darstellung einer Zahl im Binärsystem werden die Ziffern wie auch im Dezimalsystem ohne Trennzeichen hintereinander geschrieben. Ihr Stellenwert entspricht der zur Stelle passenden Zweierpotenz. Die höchstwertige Stelle wird ganz links und die niederwertigeren Stellen in absteigender Reihenfolge rechts davon aufgeschrieben.
Wenn man im Dezimalsystem zählt, erhöht man die letzte Stelle immer um 1. Wenn es nicht mehr weiter geht, weil man bei der höchsten Ziffer angekommen ist, setzt man sie auf 0 und erhöht die Ziffer davor. Wenn diese Ziffer die größtmögliche Ziffer ist - wie bei 99 - wird auch diese auf 0 gesetzt und die Ziffer davor erhöht. Und so weiter.
Im Binärsystem macht man es genauso: Nach 0 kommt 1, danach wird die 1 auf 0 gesetzt und die Stelle davor erhöht.
Dezimal: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
Binär: | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 |
Rechnen im Binärsystem
Ein Computer rechnet ständig mit Binärzahlen. Sie werden addiert, subtrahiert, multipliziert und dividiert. Im Grunde funktioniert das ähnlich wie in unserem Dezimalsystem.
Bei der Addition gilt:
mit Übertrag:
Bei der Subtraktion gilt:
mit Übertrag
Umrechnung in das Dezimalsystem
Auch das Binärsystem ist - wie das Dezimalsystem - ein Stellenwertsystem. Daher kann man von einer gegebenen Binärzahl auf die gleiche Weise den Gesamtwert als Dezimalzahl ermitteln. Das heißt, jede Stelle der Zahl hat eine bestimmte Wertigkeit. Wenn man die Stellen nun durchnummeriert und bei den Einern mit 0 beginnt, kann man die Wertigkeit der einzelnen Stellen sehr schön mit der Basis 2 ausdrücken:
| |
|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Beispiel: Umrechnung Binärzahlzahl: 101 in Dezimal
Binärzahl: | 1 | 0 | 1 |
|---|---|---|---|
Stellennummer: | 2 | 1 | 0 |
Stellenwert: |
|
|
|
Potenzwert: |
|
|
|
Anwendungen
Wie schon im Abschnitt Definition erläutert ist das Binärsystem Basis aller unserer Computersysteme. Auch die Speicherung von Daten auf Festplatten und andere Speichermedien funktionieren nach diesem Prinzip. Leider gibt es in der heutigen Zeit keine aktuell verfügbaren Massenspeichergeräten, die uns als Mensch in die Lage versetzen, die Daten sehen zu können. Schaut man sich jedoch ein wenig in der Geschichte der Speichermedien um, wird man schnell bei Lochkarte oder eben auch dem Lochstreifen fündig.
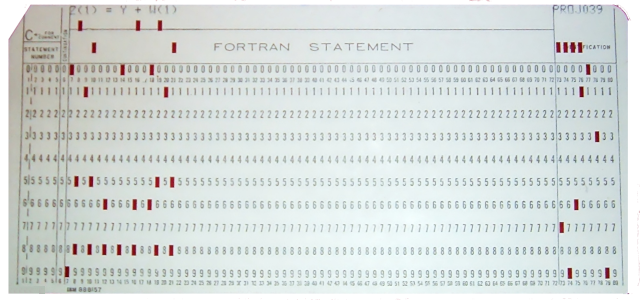
Bild_1: Lochkarte mit FORTRAN Statement
Quelle: Wikibooks Computerhardware Speicher, Foto: Arnold Reinhold [2]
Erläuterung der Codierung von Daten beispielhaft an einem Lochstreifen:

Bild_2: Lochstreifen mit Beispiel Codierung "Hello World!"
Quelle: Robotron Computermuseum [3]
Der Lochstreifen im Bild (Bild_2) ist in einem ANSI 7bit Code [4] gestanzt. Die kleineren Löcher nach der 3. Zeile ist der Transportstreifen, mit dem das Papier im Gerät transportiert wird. Das 8. Datenloch (unterste Zeile) ist mit einem Paritätsbit belegt und dient nur der Überprüfung der anderen 7 Bits [5].
Das Decodieren des Lochstreifencodes erfolgt mit Hilfe der Löcher, durch die die Binärzahlen in folgender Form codiert sind:
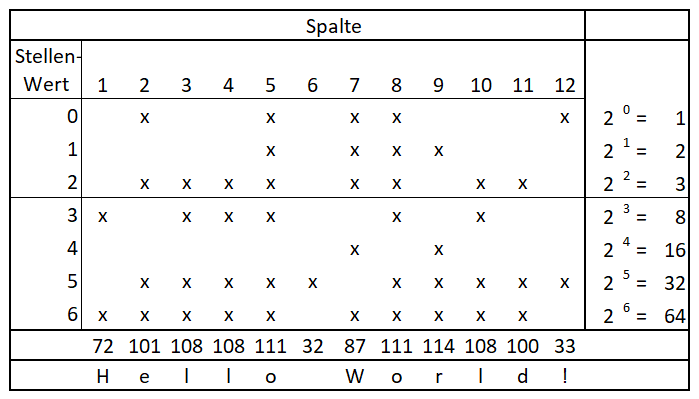
Vergleicht man die Löcher von Bild (Bild_2) mit dem Zeichen "x" in der Darstellung, stellt man fest, dass das genaue Lochmuster des Lochstreifens hier in der Darstellung abgebildet ist. Rechnet man die erste Spalte exemplarisch, kommt man zu folgendem Ergebnis:
Es befinden sich 2 Löcher an dieser Spalte. Loch 1 direkt unterhalb des Transportstreifens und Loch 2 auf der untersten Lochlinie (beachte Paritätsbit).
Somit haben wir ein Loch auf den Stellenwerten 3 und eines auf 6:
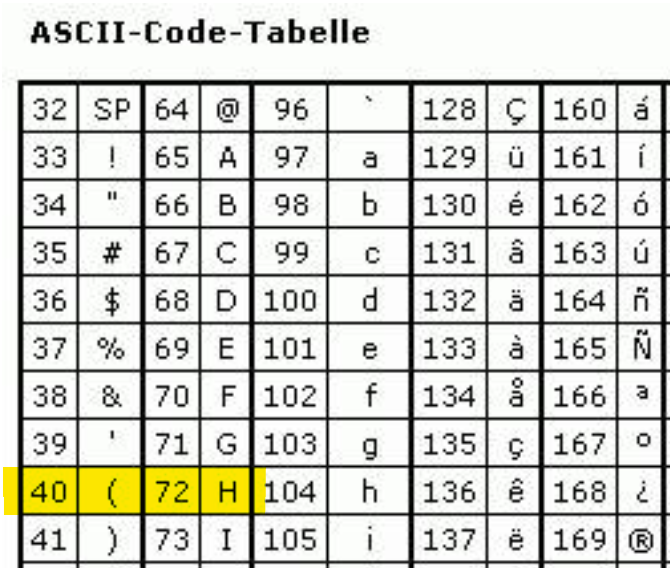
Um die Zahl in ein Zeichen umzurechnen, braucht man Informationen aus einer ASC-II Tabelle. Diese Tabelle dient als Grundlage für Kodierungen von Zeichensätzen. In ihr ist jeder Zahl in einem vorgegebenen Bereich ein Buchstabe oder Zeichen zugeordnet. [6]
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu Zahlensystemen
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
Artikel
- Zahlensysteme
- Stellenwertsysteme
- Dezimalsystem
- Oktalsystem
- Additionssysteme
- Hybridsysteme
- Hexadezimalsystem
- Römische Zahlen
