Das Halteproblem

An deinem ersten Arbeitstag als Informatiker:in in einer Softwarefirma bekommst du von der Geschäftsleitung den Auftrag: Schreibe bis nächste Woche ein Programm, das als Eingabe eine Turingmaschine $T$ (in codierter Form) und ein Wort $w$ erhält und das prüft, ob die Turingmaschine, wenn sie das Wort $w$ abarbeitet, irgendwann zu einem Ende kommt ("hält"). Eine Turingmaschine ist eine sehr einfache (gedankliche) Maschine, die aber gleichwohl alles berechnen kann, was auch ein Computer berechnen kann.

Du setzt dich also hin, überlegst dir zuerst, wie du eine Turingmaschine geeignet für die Eingabe codierst, wie du sie anschließend am besten im Programm repräsentierst, welche Funktionen du brauchst, um sie zu simulieren – doch stopp! Genau das tust du nicht!

Denn als Informatiker:in weißt du:

Das Programm, das du schreiben sollst, gibt es nicht. Die von der Geschäftsleitung wollten sich einen kleinen Scherz mit dir erlauben. Sehr witzig! Und das an deinem ersten Arbeitstag.

Das Halteproblem

Etwas technischer formulierst du das Halteproblem als Wortproblem einer Sprache.

Um aus dem Halteproblem ein Wortproblem zu machen, überlegst du dir zuerst eine geeignete Codierung für Turingmaschinen. Beispielsweise schreibst du die Zeilen der Turingtabelle einfach alle hintereinander – fertig. Und dann definierst du die Sprache $L$ wie folgt:

$L ~=~ \{ Tw ~|~ \text{die Turingmaschine} ~T~ \text{ hält mit dem Eingabewort}~ w~ \}$

Jedes Wort $x$ in der Sprache $L$ besteht also aus einer (codierten) Turingmaschine $T$ gefolgt von einem Wort $w$, mit der Eigenschaft, dass diese Turingmaschine $T$ irgendwann hält, wenn sie das Wort $w$ als Eingabewort abarbeitet.

Tatsächlich ist das Wortproblem für diese Sprache nicht entscheidbar; dies bedeutet, dass es keine Turingmaschine $M$ gibt, die

• jedes Wort $x$, das in $L$ liegt, akzeptiert und

• jedes Wort $x$, das nicht in $L$ liegt, zurückweist.

Warum gibt es eine solche Turingmaschine $M$ nicht?

Tatsächlich gibt es wohl eine Turingmaschine $M$, die jedes Wort $x$, das in $L$ liegt, akzeptiert: Die Turingmaschine $M$ simuliert die entsprechende Turingmaschine $T$ mit dem entsprechenden Eingabewort $w$. Da $T$ irgendwann hält, endet die Simulation an dieser Stelle und $M$ hält auch und akzeptiert.

Aber warum gibt es keine Turingmaschine $M$, die jedes Wort $x$, das nicht in $L$ liegt, zurückweist?

Sie könnte doch als Erstes prüfen, ob $T$ eine gültige Turingmaschine ist. Wenn nein, würde sie das Wort zurückweisen.

Und wenn ja, würde sie die Turingmaschine $T$ mit dem Eingabewort $w$ simulieren, und sie würde Buch führen über alle Konfigurationen, die dabei auftreten. Sobald eine Konfiguration zum wiederholten Mal auftritt, weist sie das Wort zurück, denn dann befindet sich $T$ in einer Endlosschleife und hält nicht.

Eine Konfiguration ist sozusagen eine Momentaufnahme der Arbeit der Turingmaschine. Eine Konfiguration besteht aus

• dem Wort, das auf dem Arbeitsband steht,

• der Stellung des Cursors auf dem Arbeitsband und

• dem Zustand, in dem sich die Turingmaschine befindet.

Das Problem ist, dass es unendlich viele mögliche Konfigurationen gibt. Denn die Turingmaschine $T$ kann beliebig viele Zeichen auf das Arbeitsband schreiben. Es kann sein, dass die Turingmaschine endlos läuft, aber dass keine Konfiguration zum wiederholten Mal auftritt.

Die Turingmaschine $M$ würde dann also ebenfalls, wie die Turingmaschine $T$, die sie simuliert, endlos weiterlaufen.

Ein formaler Beweis per Diagonalisierung

Es könnte natürlich möglich sein, dass es eine ausgeklügeltere Methode gibt, um festzustellen, dass die Turingmaschine $T$ mit Eingabewort $w$ nicht hält. Aber tatsächlich ist dies nicht der Fall. Der Beweis benutzt das zweite Cantorsche Diagonalverfahren, ähnlich wie der Beweis, dass die Menge der reellen Zahlen nicht abzählbar ist.

Zugrundegelegt ist ein beliebiges Eingabealphabet $A$. In der folgenden Tabelle sind

• die Zeilen mit allen Turingmaschinen, die es gibt, beschriftet und

• die Spalten mit allen Wörtern über dem Alphabet $A$, die es gibt, beschriftet.

Da es abzählbar viele Turingmaschinen gibt und ebenfalls abzählbar viele Wörter, ist dies möglich.

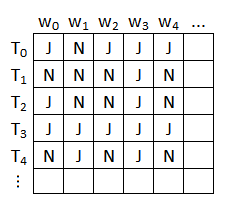
Ein Tabelleneintrag an Position $(i, j)$ lautet J für "ja", wenn die Turingmaschine $T_i$ mit dem Eingabewort $w_j$ hält, und N für "nein", wenn nicht.

Angenommen, es gibt eine Turingmaschine $M$, die für jede beliebige Turingmaschine $T$ und für jedes beliebige Wort $w$ entscheidet, ob $T$ mit Eingabewort $w$ hält oder nicht. Dann könnte $M$ alle Einträge der Tabelle berechnen.

Mithilfe von $M$ lässt sich nun eine Turingmaschine $X$ konstruieren, die mit beliebigem Eingabewort $w_j$ hält, wenn die Turingmaschine $T_j$ mit $w_j$ nicht hält, und umgekehrt mit Eingabewort $w_j$ nicht hält, wenn $T_j$ mit $w_j$ hält. Hierbei ist $T_j$ die Turingmaschine in Zeile $j$, wobei $j$ die Spalte von $w_j$ ist.

Die Turingmaschine $X$ kommt irgendwo in der Tabelle vor. In der Zeile der Turingmaschine $X$ steht das Komplement der Diagonalen der Tabelle, also statt J jeweils ein N und statt N ein J.

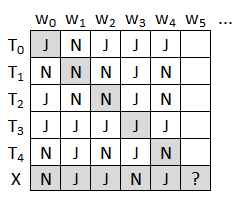
Aber das kann nicht sein, da die Zeile irgendwo die Diagonale schneidet und in dem betreffenden Tabelleneintrag dann ein J aus der Zeile und ein N aus der Diagonalen oder umgekehrt stehen würde – ein Widerspruch.

Der Widerspruch kommt dadurch zustande, dass die Annahme falsch ist.

Was folgt daraus?

Wenn du ein Programm schreibst, dann überprüft der Compiler, ob dein Programm syntaktisch korrekt ist, also den Regeln der Programmiersprache entspricht. Wenn du irgendwo eine schließende Klammer vergessen hast oder einen Funktionsnamen falsch geschrieben hast, bekommst du eine Fehlermeldung.

Wenn du die Fehler beseitigt hast und dein Programm läuft, dann kann es passieren, dass es läuft und läuft und läuft - du hast versehentlich eine Endlosschleife programmiert.

Auch dem genialsten Programmierer unterläuft so etwas gelegentlich. Wäre es da nicht sinnvoll, wenn der Compiler gleich mitprüfen würde, ob das Programm terminiert, also irgendwann zum Ende kommt?

Sinnvoll wäre es, aber möglich ist es leider nicht. Jedenfalls nicht im allgemeinen Fall, dies ist die Konsequenz aus der Nichtentscheidbarkeit des Halteproblems.

Eine anschauliche Erklärung

Angenommen, die folgende Funktion existiert:

Wenn du diese Funktion aufrufst, übergibst du ihr einen Programmtext $p$ als Parameter. Die Funktion prüft dann, ob das entsprechende Programm terminiert. Wenn ja, gibt sie true zurück, wenn nein, gibt sie false zurück.

Nun schreibst du folgende Funktion test:

Die Funktion enthält eine While-Schleife mit leerem Schleifenkörper. In der Schleifenbedingung rufst du die obige Funktion halts auf und übergibst ihr dein Programm test als Parameter.

 Was passiert nun, wenn du die Funktion test aufrufst? Du kannst zwei Fälle unterscheiden:

• test terminiert $\Rightarrow$ halts liefert true $\Rightarrow$ While-Schleife läuft endlos $\Rightarrow$ test terminiert nicht

• test terminiert nicht $\Rightarrow$ halts liefert false $\Rightarrow$ While-Schleife wird sofort verlassen $\Rightarrow$ test terminiert

In beiden Fällen erhältst du also einen Widerspruch. Dieser Widerspruch kommt dadurch zustande, dass die Annahme falsch ist. Die Funktion halts gibt es nicht!

(Quelle: D. Gries, F.B. Schneider: A Logical Approach to Discrete Math. Springer (1994))