Aufgaben zu Iterationsschemata

Berechnung von $π$

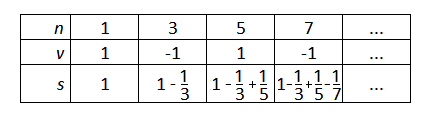
Die Leibniz-Reihe konvergiert (allerdings sehr langsam) gegen den Grenzwert $π / 4$ :

\frac{π}{4} = 1 – \frac{1}{3} + \frac{1}{5} – \frac{1}{7} + \frac{1}{9} – \frac{1}{11} + \frac{1}{13} – . . .

Stelle ein Iterationsschema für die Berechnung von $π / 4$ auf. Leite daraus die zugehörigen Initialisierungen und Iterationsgleichungen ab.

Das Iterationsschema stellst du in folgender Weise auf. Du brauchst drei Variablen: $n$ für den Nenner, $v$ für das Vorzeichen und $s$ für die Summe.
Aus dem Iterationsschema leitest du die Iterationsgleichungen ab, .
$n = n^{'} + 2$
$v = - v^{'}$
$s = s^{'} + v / n$
Die Werte in der ersten Spalte des Iterationsschemas legst du durch Initialisierung fest:
$n = 1$
$v = 1$
$s = 1$
Das war's. Jetzt leitest du daraus unmittelbar ein Programm mit einer While-Schleife ab.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Setze die Ergebnisse aus der vorherigen Teilaufgabe in eine While-Schleife um. Brich die While-Schleife ab, wenn der Wert von $n$ größer oder gleich 10.000 wird.
Erstelle unter Benutzung dieser While-Schleife eine Funktion pi() zur (grob angenäherten) Berechnung von $π$ .

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Hast du eine Frage oder Feedback?