Aufgaben zur Hinführung auf schwierige Extremwertprobleme

Gegeben sei ein gleichseitiges Dreieck mit der Seitenlänge $a\,\text{LE}$ .

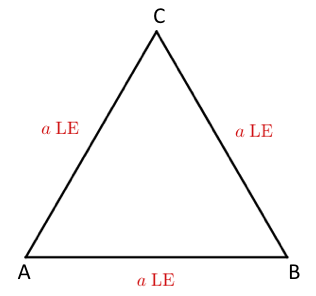
Auf welche Weise kann man dem Dreieck Rechtecke einbeschreiben?
Klicke die richtige Antwort an.
- Dem Dreieck können Rechtecke so einbeschrieben werden, dass auf jeder der Dreiecksseiten eine Rechtecksseite liegt.
- Einem gleichseitigen Dreieck kann auf keine Weise ein Rechteck einbeschrieben werden.
- Dem Dreieck können Rechtecke nur so einbeschrieben werden, dass eine Rechtecksseite auf der Grundlinie $[AB]$ des Dreiecks liegt.
Für diese Aufgabe benötigst Du folgendes Grundwissen: gleichseitiges Dreieck
Einem Dreieck ein Rechteck "einbeschreiben" bedeutet, dass jeder Eckpunkt des Rechtecks auf einer Dreiecksseite liegt. Zwei Eckpunke des Rechtecks müssen dann auf derselben Dreiecksseite liegen. Dafür kommt jede Dreiecksseite in Frage.
Also kann man einem gleichseitigen Dreieck auf dreifache Weise Rechtecke einbeschreiben.
Verschiebe zur Veranschaulichung im gegebenen Applet die Gleiterpunkte $P_1$ , $P_2$ , $P_3$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne den größtmöglichen Flächeninhalt eines Rechtecks, das dem Dreieck einbeschrieben werden kann.
Wie viel Prozent der Dreiecksfläche besitzt solch ein maximales Rechteck?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe
In dieser Aufgabe soll einem gleichseitigen Dreieck ein möglichst großes Rechteck einbeschrieben werden.
Lösungsstrategie:
Du berechnest als erstes die Höhe des gleichseitigen Dreiecks. Entweder mit Hilfe des Satzes des Pythagoras oder du entnimmst sie einer Formelsammlung.
Dann kannst du - ohne Koordinatensystem - die Nebenbedingung der Extremwertaufgabe mit Hilfe des Strahlensatzes aufstellen.
Höhe im gleichseitigen Dreieck (Pythagoras):
$\def\arraystretch{1.25} \begin{array}{rcl}h^2+\left(\frac{a}{2}\right)^2&=&a^2\\h^2&=&a^2-\left(\frac{a}{2}\right)^2\\h^2&=&\frac 34a^2\\h&=&\frac a 2\sqrt 3\end{array}$
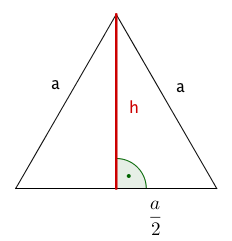
Zielfunktion sei die Formel für den Flächeninhalt eines Rechtecks mit den Seitenlängen $x\,LE$ und $y\,LE$ :
$A(x;y)=x\cdot y$
Die Nebenbedingung für $x$ und $y$ ergibt sich aus dem Strahlensatz:
$\displaystyle \frac {x} {a} = \frac {\frac{1}{2} a \sqrt{3}-y} {\frac{1}{2} a \sqrt{3}}$
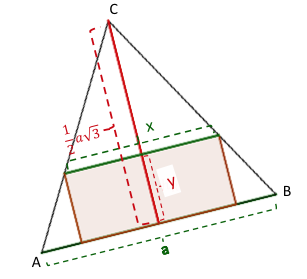
Löse die Gleichung nach $y$ auf.
$\def\arraystretch{1.25} \begin{array}{rcll}\frac{x}{a}&=&\frac{\frac{1}{2} a \sqrt{3}-y}{\frac{1}{2} a \sqrt{3}}&|\cdot \frac{1}{2}a \sqrt{3}\\\frac{x}{2} \sqrt{3}&=&\frac{1}{2} a \sqrt{3}-y&|+y-\frac{x}{2}\ \sqrt{3}\\y&=&\frac{1}{2} \sqrt{3}\left(a-x\right)\end{array}$
Setze $y$ in die Zielfunktion $A(x;y)=x \cdot y$ ein:
$\def\arraystretch{1.25} \begin{array}{rcl} A(x)&=&x\cdot\frac{1}{2} \sqrt{3}(a-x)\\A(x)&=&-\frac{1}{2} \sqrt{3}\cdot x^2+\frac{1}{2}\sqrt{3}\cdot a\cdot x\end{array}$
$\mathbb{D}_A=]0;a[$
Bilde $A'(x)$ .
$A'(x)=- \sqrt{3}\cdot x+\frac{1}{2} \sqrt{3}\cdot a$
$A'(x)=\sqrt{3}(\frac 12a-x)$
Setze $A'(x)$ gleich Null.
$\def\arraystretch{1.25} \begin{array}{rrcl}&\sqrt{3}(\frac 12a-x)&=&0\\ \Rightarrow &x&=&\frac{1}{2}a\end{array}$
Überprüfe, ob $A''(0{,}5a)$ negativ ist, damit sich ein Maximum ergibt.
$A''(x)=- \sqrt{3}$
Ergebnis:
Die Breite des gesuchten flächengrößten Rechtecks ist gerade halb so groß wie die Seitenlänge des Dreiecks.
Für die Höhe $y$ ergibt sich:
$y=\frac 12 \sqrt{3}\cdot \frac12 a=\frac{a}{4}\sqrt{3}$
Für die Fläche des gesuchten größten Rechtecks gilt:
$\displaystyle A_{max}=\frac {a}{2}\cdot \frac{a}{4} \sqrt{3}= \frac{a^2}{8}\sqrt{3}$
Der Flächeninhalt dieses Rechtecks ist gerade 50 Prozent der Dreiecksfläche, denn für diese gilt:
$A_{Dreieck}= \frac 12 \cdot a\cdot \frac{a}{2} \sqrt{3}=\frac{a^2}{4} \sqrt {3}$ .
Erweiterung der Aufgabenstellung:
Aus der Punktsymmetrie eines gleichseitigen Dreiecks zu seinem Mittelpunkt folgt, dass alle drei einbeschreibbaren maximalen Rechtecke gleich groß sind.
Im nachstehenden Applet kannst du dies grafisch nachvollziehen, indem du die verschiedenen Gleiterpunkte verschiebst.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Beschreibe einem gleichseitigen Dreieck (Seitenlänge $5\, cm$ ) drei verschiedene gleichgroße Rechtecke mit dem Inhalt von jeweils $4\,cm^2$ ein.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe
In dieser Aufgabe sind die Flächeninhalte der einzubeschreibenden Rechtecke vorgegeben. Folgender Lösungsplan für die Konstruktion ist möglich:
Über jeder Dreiecksseite kann es zwei verschiedene Rechtecke mit dem gleichen Inhalt von $4\,LE$ geben. Konstruiere also z.B. diese beiden über der Dreiecksseite $[AB]$ und ein drittes über der Dreiecksseite $[AC]$ .
Bevor du konstruierst, musst du die Rechtecksseiten $x\,LE$ und $y\,LE$ berechnen. Benutze dazu eine Zielfunktion und die Nebenbedingung wie in der vorausgehenden Teilaufgabe b).
Durchführung:
Zielfunktion
$A(x;y)=x\cdot y$
Nebenbedingung
$y=-\frac12 \sqrt{3}x+\frac 52 \sqrt{3}\;\Rightarrow$
$y=\frac 12 \sqrt{3}\left(-x+5\right)$
Setze in der Zielfunktion für $A(x;y)$ den Wert 4 und für y den Term der Nebenbedingung ein und ordne die entstehende quadratische Gleichung.
$\def\arraystretch{1.25} \begin{array}{rcll}x\cdot\frac 12 \sqrt{3}(-x+5)&=&4&\\\frac 12 \sqrt{3}x^2-\frac 52 \sqrt{3}+4&=&0&|:\frac 12 \sqrt{3}\\x^2-5x+\frac {8}{\sqrt{3}}&=&0&\end{array}$
Löse die Gleichung mit der Mitternachtsformel und runde die Ergebnisse.
$x_1\approx{3{,}77}$
$x_2\approx{1{,}22}$
Berechne die zugehörigen y-Werte.
$y_1\approx{\frac 12 \sqrt{3}(-3{,}77+5)}\approx{1{,}06}$
$y_2\approx{\frac 12 \sqrt{3}(-1{,}22+5)} \approx3{,}27$
Zur Konstruktion der Rechtecke benutzt du die berechneten y-Werte:
Rechteck 1 über $[AB]$ :Zeichne eine Parallele zu $[AB]$ im Abstand 1,06. Schneide diese mit den Dreiecksseiten $[AC]$ und $[BC]$ und ergänze zum Rechteck.
Analog erhältst du das Rechteck 2 über $[AB]$ durch eine Parallele im Abstand 3,27.
Das Rechteck 3 über der Seite $[AC]$ erhältst du durch die Parallele im Abstand 1,06 zu $[AC]$ und die entsprechende Ergänzung zum Rechteck.
Die einzelnen Konstruktionsschritte kannst du im folgenden Applet schrittweise nachvollziehen. Benutze dazu die untere Navigationsleiste.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Tipp: Berechne mit Hilfe des Strahlensatzes die Nebenbedingung für das Einbeschreiben von Rechtecken in ein gleichseitiges Dreieck (oder entnimm die Formel der vorangehenden Aufgabe). Berechne daraufhin aus der Flächenformel für das Rechteck mit der sich ergebenden quadratischen Gleichung die möglichen Seitenlängen.
Runde die Ergebnisse auf ein sinnvolles Maß und konstruiere damit die gesuchten möglichen Rechtecke.

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?