Aufgaben zu wichtigen Begriffen bei Funktion

Hier wird die Nullstelle erst graphisch und dann rechnerisch bestimmt.

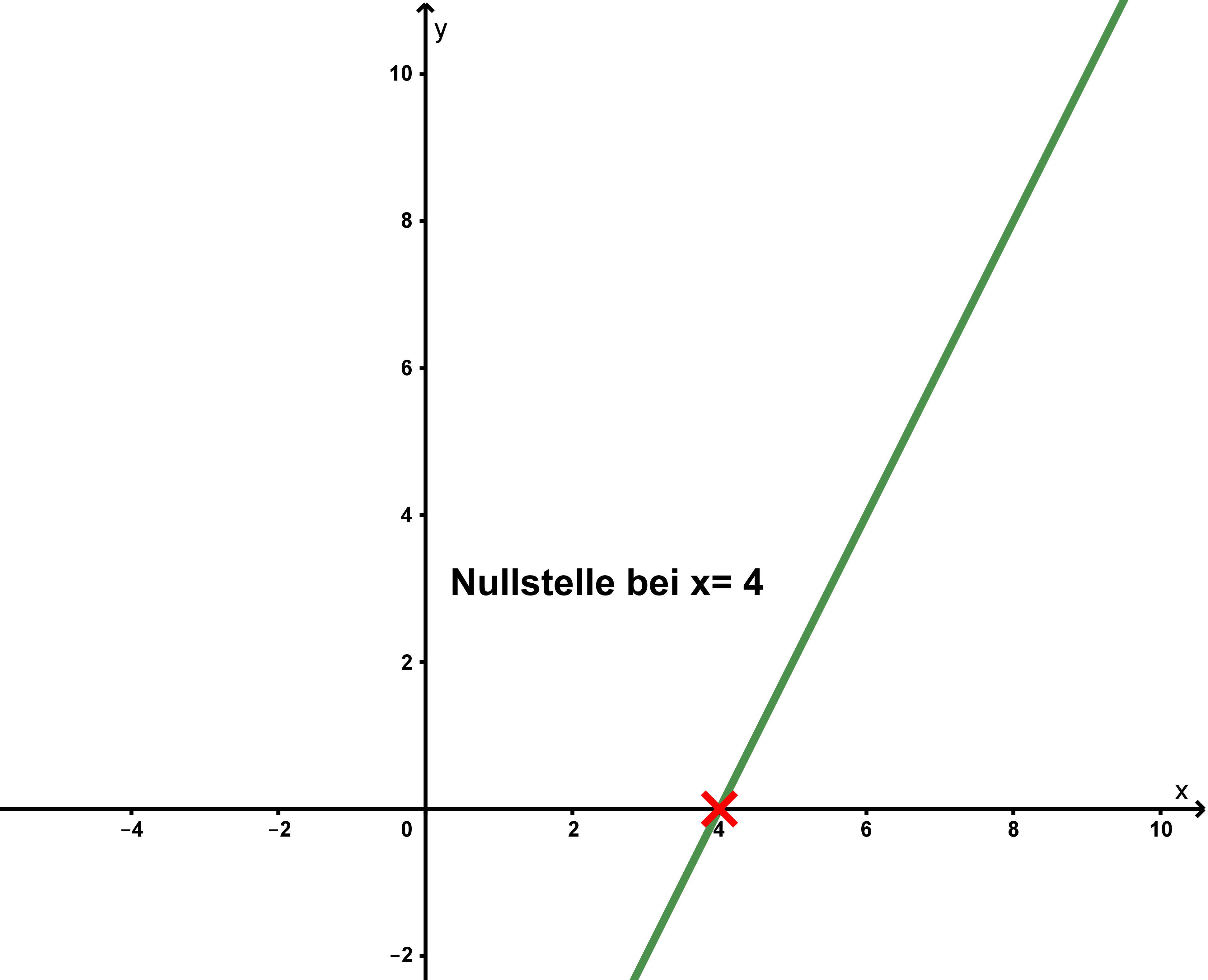
Man sieht, dass der Graph der Funktion $f$ die x-Achse genau im Punkt (4|0) schneidet.

$\Rightarrow$ Nullstelle bei $x=4$.

Graphische Veranschaulichung:

Lösung durch Berechnung:

Die Nullstelle der Funktion liegt bei $x=4$.

Hier werden die Nullstellen erst graphisch und dann rechnerisch bestimmt.

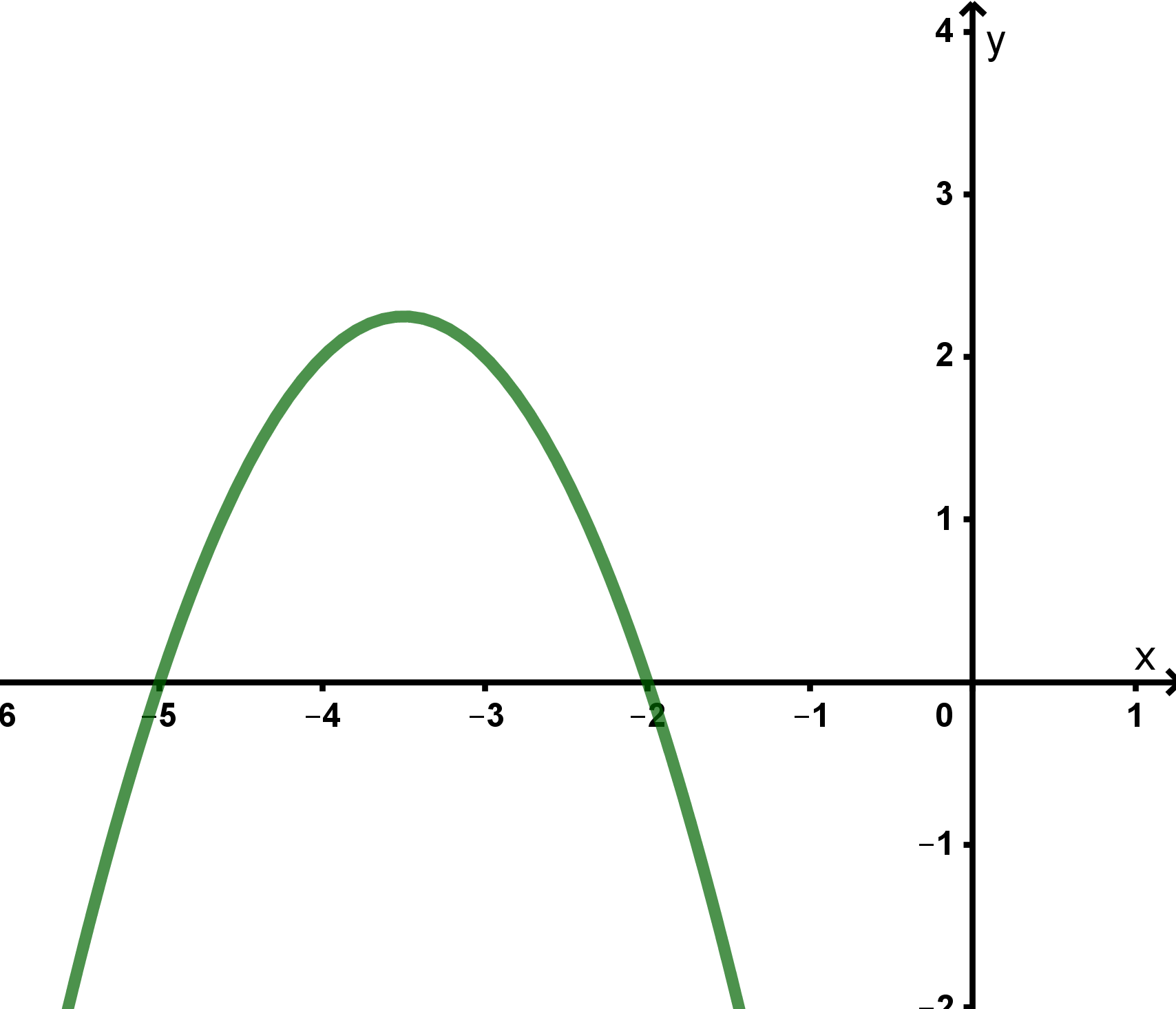
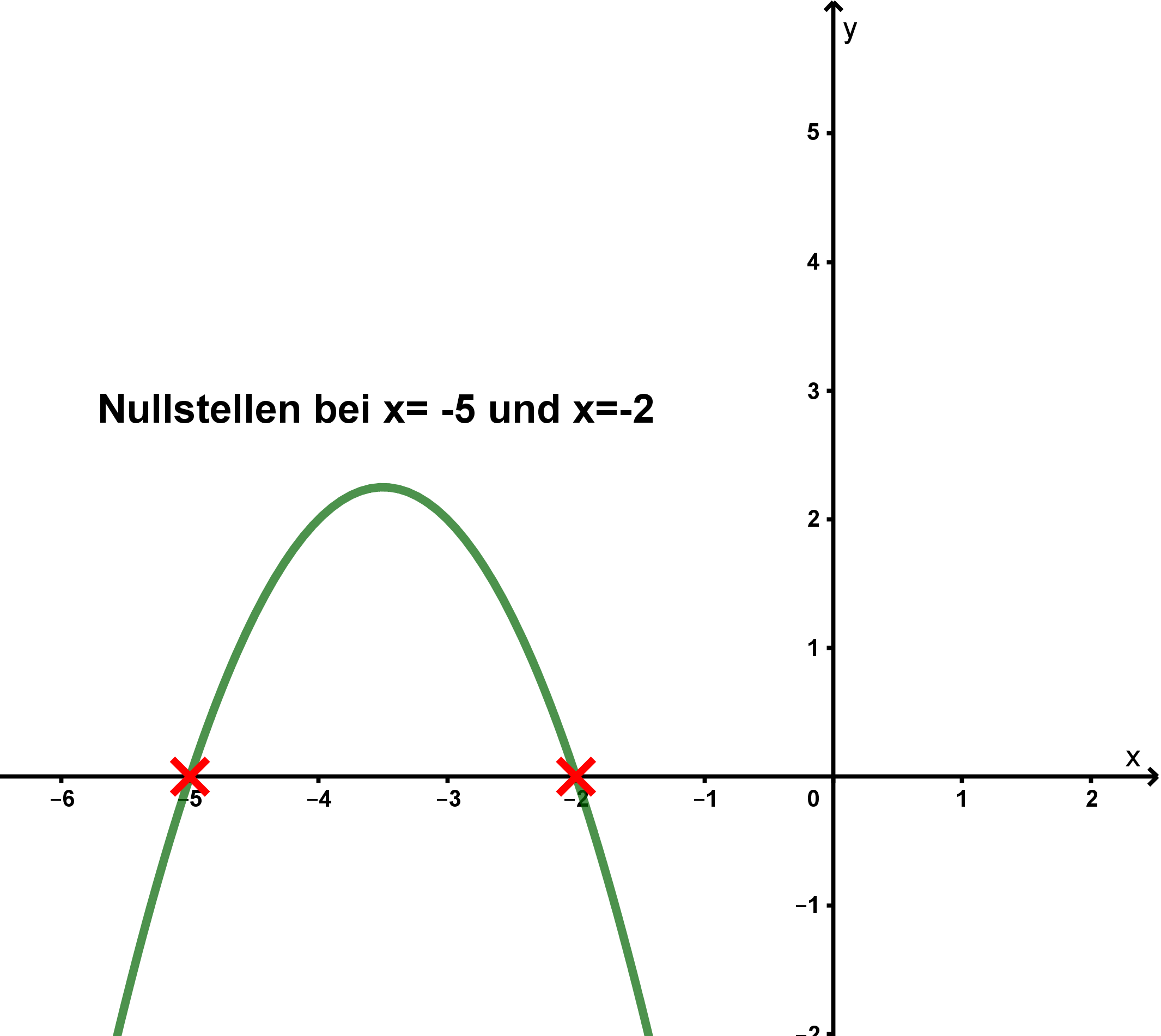
Man sieht, dass der Graph der Funktion f die x-Achse genau in den Punkten (-5|0) und (-2|0) schneidet.

⇒ Nullstellen bei $x=-5$ und $x=-2$

Graphische Veranschaulichung:

Lösung durch Berechnung:

Die beiden Nullstellen der Funktion liegen bei $x_1=-5$ und $x_2=-2$.

Hier werden die Nullstellen erst graphisch und dann rechnerisch bestimmt.

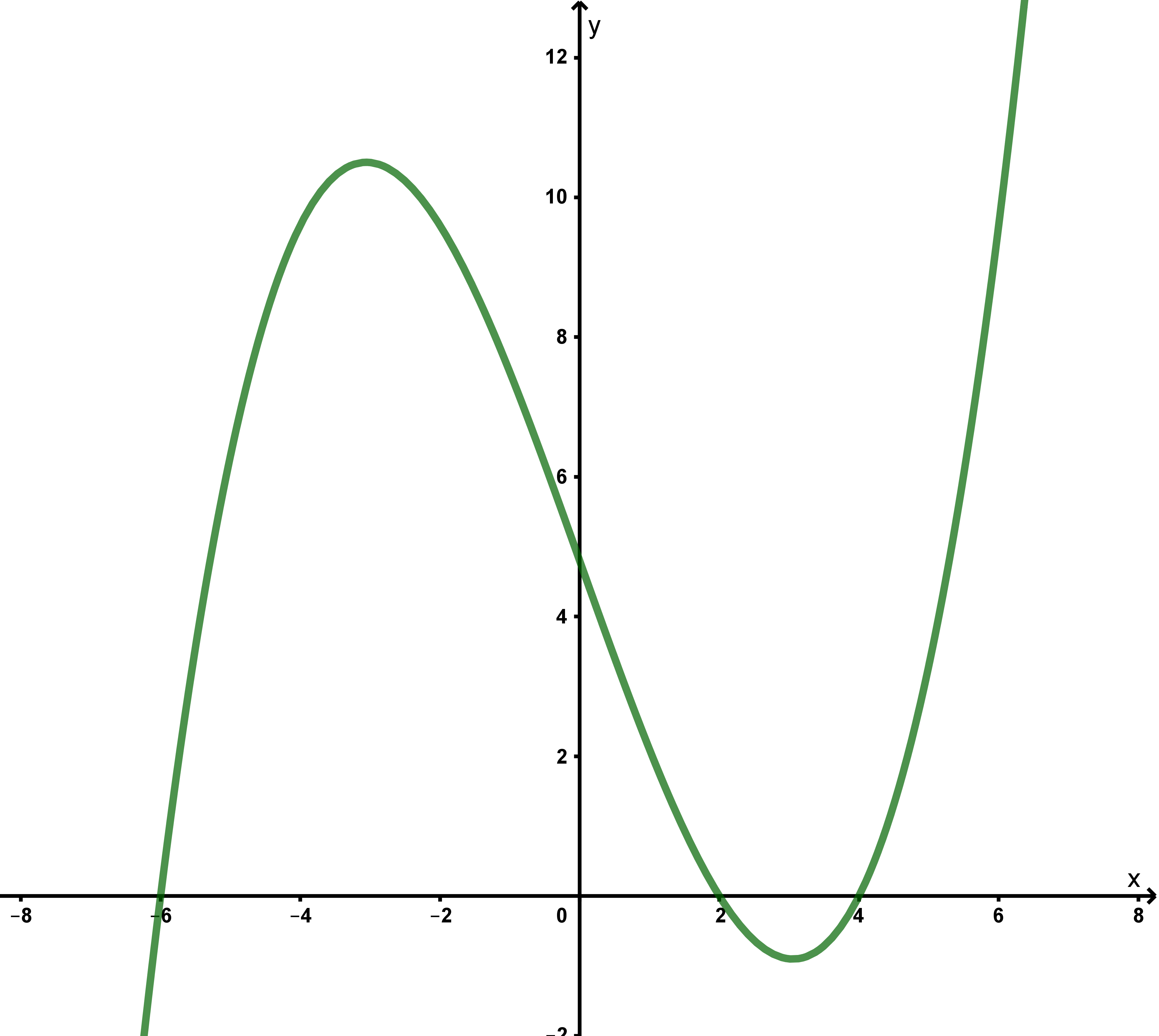
Man sieht, dass der Graph der Funktion $f$ die x-Achse genau in den Punkten (-6|0), (2|0) und (4|0) schneidet.

⇒ Nullstellen bei $x=-6$und $x=2$ und $x=4$.

Graphische Veranschaulichunng

Lösung durch Berechnung:

Für $x=-6$, $x=2$ und $x=4$ gilt:

$\frac{1}{10}(x+6)(x-2)(x-4)=0$

Die Nullstellen der Funktion liegen bei $x=-6$, $x=2$ und $x=4$.

Hier werden die Nullstellen erst graphisch und dann rechnerisch bestimmt.

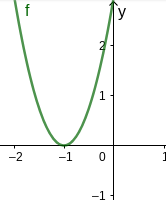
Man sieht, dass der Graph der Funktion f die x-Achse genau in einem Punkt (-1|0) berührt.

⇒ Nullstelle bei x=−1.

Graphische Veranschaulichung

Lösung durch Berechnung

$x_{\mathrm{1,2}}=\frac{-2\pm \sqrt{(2{)}^2-4\cdot 1\cdot 1}}{2\cdot 1}$

$x_{\mathrm{1,2}}=\frac{-2\pm \sqrt{0}}{2\cdot 1}=\frac{-2\pm 0}{2}=-1$

$\Rightarrow x_1=-1$

Die Nullstelle liegt also bei $x_1=-1$.