In Analogie zu einem Spielwürfel wird ein quaderförmiger Tafelschwamm geworfen.

Für das einmalige Werfen des Schwammes wurde experimentell folgendes Modell ermittelt:
Elementarereignis | "Eine der beiden größten Seitenflächen oben" | "Eine der beiden kleinsten Seitenflächen oben" | "Eine der beiden übrigen Seitenflächen oben" |
|---|---|---|---|
Wahrscheinlichkeit | 0,83 | 0,04 | 0,13 |
Beschreibe, wie man experimentell einen Schätzwert für die Wahrscheinlichkeit des Ereignisses „Der Tafelschwamm landet bei einmaligem Werfen so, dass eine der beiden kleinsten Seitenflächen oben liegt.” ermitteln kann. (1 BE)
Begründe anhand der Tabelle, dass dieses Zufallsexperiment kein Laplace-Experimentist. (1 BE)
Der abgebildete Schwamm wird einmal geworfen. Gib ein Ereignis an, dessenWahrscheinlichkeit 87% beträgt. (1 BE)
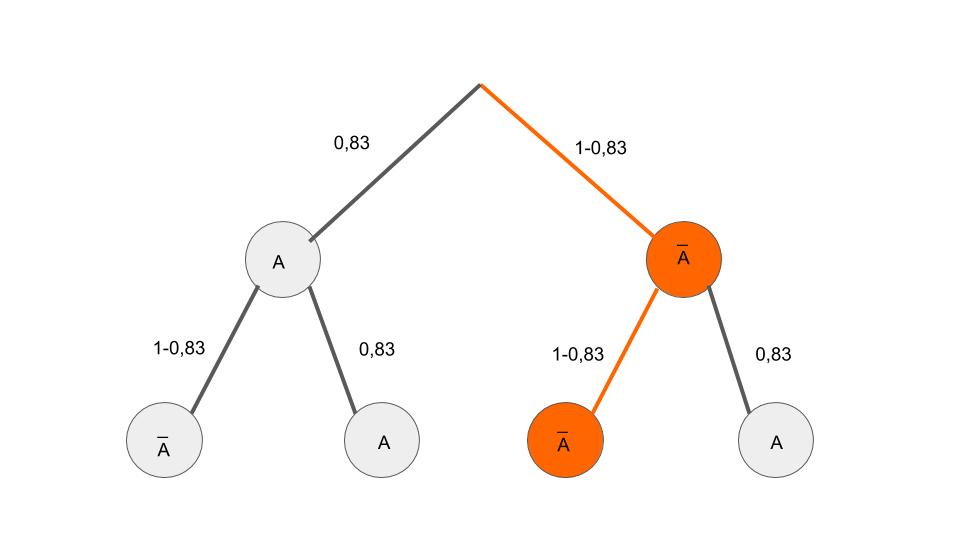
Der abgebildete Schwamm wird zweimal geworfen. Kreuz an, mit welcher Wahrscheinlichkeitder Schwamm dabei nie auf eine der beiden größten Seitenflächen fällt. (1 BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?