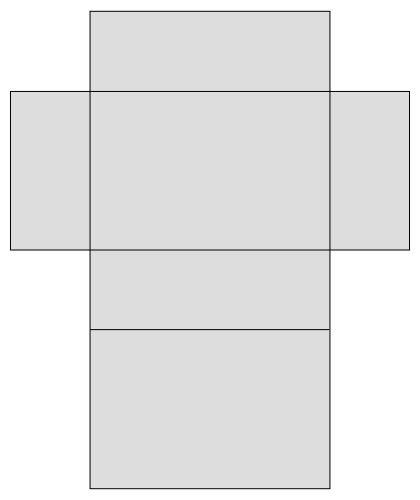
Max möchte ein Paket verschicken. Für muss er 1,50€ bezahlen. Sein Paket ist 20 cm hoch, 30 cm breit und 15 cm lang. Wieviel Pappe braucht er und wieviel muss er dafür bezahlen?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?