Gemischte Aufgaben - lernen mit Serlo!

Ein Wandergebiet ist von vielen Wanderwegen durchzogen. Legt man dieses Wandergebiet in ein Koordinatensystem, so kann man seine Zielposition mithilfe von Vektorketten berechnen.

Du beginnst eine Wanderung an einem Parkplatz, der ausgehend vom Ursprung die Koordinaten $P (1 ∣ - 2 ∣ 0,5)$ hat. Danach bewegst du dich 2,7 km entlang eines Weges, der durch den Vektor $\vec{w_1} = \begin{pmatrix} 8\\4\\1\end{pmatrix}$ ausgedrückt wird, bevor du vorzeitig auf einen anderen Weg $\vec{w_2} = \begin{pmatrix} -11\\-10\\2\end{pmatrix}$ abbiegst und diesem 1,5 km folgst. Danach steigst du in eine Talbahn und fährst 1,8 km einen Weg entlang, der im Koordinatensystem durch $\vec{w_3} = \begin{pmatrix} 1\\8\\-4\end{pmatrix}$ beschrieben wird, bevor du an einer Zwischenstation aussteigst.

Bestimme die Koordinaten des Berggasthofes $B$ , bei dem du deine Wanderung beendest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Länge von Vektoren anpassen
Der zu berechnende Term
Um zum Berggasthof zu gelangen, muss man vom Parkplatz aus die veränderten Vektoren, die den Wanderwegen entsprechen, abgehen.
Keine Angst, der Term wird in den nächsten Schritten nochmal Stück für Stück aufgeschlüsselt und erklärt.
$\vec{B}=\vec{P}+\frac{2{,}7}{\left|\vec{w_1}\right|}\cdot\vec{w_1}+\frac{1{,}5}{\left|\vec{w_2}\right|}\cdot\vec{w_2}+\frac{1{,}8}{\left|\vec{w_3}\right|}\cdot\vec{w_3}$
Länge der Wege berechnen
Um jeden Weg auf die gewünschte Länge $k$ zu verkürzen, muss man ihn erst auf die Länge 1 verkürzen und dann wieder auf die Länge $k$ strecken. Dafür berechnest du zuerst die Länge jedes Weges, also die Länge der Vektoren.
$\left|\vec{w_1}\right|=\sqrt{8^2+4^2+1^2}LE=9\ LE$
$\left|\vec{w_2}\right|=\sqrt{\left(-11\right)^2+\left(-10\right)^2+2^2}LE=15\ LE$
$\left|\vec{w_3}\right|=\sqrt{1^2+8^2+\left(-4\right)^2}LE\ =\ 9\ LE$
Wege verkürzen
Den Quotienten aus gewünschter Länge $k_{1{,}2,3}$ und aktueller Länge $\left|\vec{w}_{1{,}2,3}\right|$ multiplizierst du jetzt bei einer skalaren Multiplikation mit dem jeweiligen Vektor $\vec{w}_{1{,}2,3}$ . Zur Übersicht kannst du die berechneten Vektoren noch benennen. Hier benennen wir sie mit $\vec{z_1},\ \vec{z_2},\vec{z_3}$ für "zurückgelegter Weg".
$\vec{z_1}=\frac{k_1}{\left|\vec{w_1}\right|}\cdot\vec{w_1}=\ \frac{2{,}7}{9}\cdot \begin{pmatrix} 8\\4\\1\end{pmatrix} = 0{,}3 \cdot \begin{pmatrix} 8\\4\\1\end{pmatrix} =\begin{pmatrix} 2{,}4\\1{,}2\\0{,}3\end{pmatrix}$
$\vec{z_2}=\frac{k_2}{\left|\vec{w_2}\right|}\cdot\vec{w_2}=\dfrac {1{,}5}{15}\cdot \begin{pmatrix} -11\\-10\\2\end{pmatrix} = 0{,}1 \cdot \begin{pmatrix} -11\\-10\\2\end{pmatrix} = \begin{pmatrix} -1{,}1\\-1\\0{,}2\end{pmatrix}$
$\vec{z_3}=\frac{k_3}{\left|\vec{w_3}\right|}\cdot\vec{w_3}=\dfrac {1{,}8}9\cdot \begin{pmatrix} 1\\8\\-4\end{pmatrix} =0{,}2\cdot \begin{pmatrix} 1\\8\\-4\end{pmatrix}= \begin{pmatrix} 0{,}2\\1{,}6\\-0{,}8\end{pmatrix}$
Vektorkette bilden
Nun kannst du die Vektoren in die Vektorkette oben einsetzen und die Koordinaten des Berggasthofes bestimmen.
$\vec{B}=\vec{P}+\frac{2{,}7}{\left|\vec{w_1}\right|}\cdot\vec{w_1}+\frac{1{,}5}{\left|\vec{w_2}\right|}\cdot\vec{w_2}+\frac{1{,}8}{\left|\vec{w_3}\right|}\cdot\vec{w_3}$
Setze zunächst an den zugehörigen Stellen die Vektoren $\vec z_1, \vec z_2,\vec z_3$ ein:
$\vec{B}=\vec{P}+\vec z_1+\vec z_2+\vec z_3$
Berechne nun den Wert des Terms, in dem du die Vektoren addierst:
$\vec B = \begin{pmatrix}1\\-2\\0{,}5\end{pmatrix}+\begin{pmatrix} 2{,}4\\1{,}2\\0{,}3\end{pmatrix}+\begin{pmatrix} -1{,}1\\-1\\0{,}2\end{pmatrix}+ \begin{pmatrix} 0{,}2\\1{,}6\\-0{,}8\end{pmatrix}=\begin{pmatrix} 2{,}5\\-0{,}2\\0{,}2\end{pmatrix}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Hier musst du einiges an Wissen verknüpfen:
Der Weg vom Parkplatz zum Gasthof ist eine Vektorkette und beginnt mit dem Ortsvektor des Parkplatzes.
Die Wege werden dabei nicht komplett durchlaufen, sondern es wird vorher abgebogen. Man muss die Vektoren also geeignet verkürzen.
Bei Wanderungen gibt man häufig an, wie viele Höhenmeter es nach oben $(\nearrow ... m)$ beziehungsweise nach unten $(\swarrow ... m)$ geht. Wie ist es bei dieser Wanderung?
Wie würdest du die Schwierigkeit der Wanderung einschätzen?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren
Mit dem Auto startet man auf einer Höhe von 500 m.
Die ersten beiden Wege führen bergauf, nämlich 0,2 km + 0,3 km, also insgesamt $\nearrow 500 m$
Der dritte Weg führt bergab, nämlich 0,8 km, allerdings werden diese nicht gelaufen (viel zu steil!) sondern mit einer Talbahn zurückgelegt. Man kann sich jetzt also streiten, ob man $\swarrow0m$ oder $\swarrow800m$ angibt.
Schwierigkeit der Route
Der Wanderweg hat recht große Steigungen und ist deshalb definitiv nichts für Anfänger, obwohl er nicht lang ist!
Im ersten Wegstück wird zum Beispiel auf 2,7 km Strecke 0,3 km Höhe gewonnen, was einer Steigung von durchgehend mehr als 10% entspricht.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Die x-3-Koordinate gibt an, wie viele Meter man nach oben bzw unten wandert.
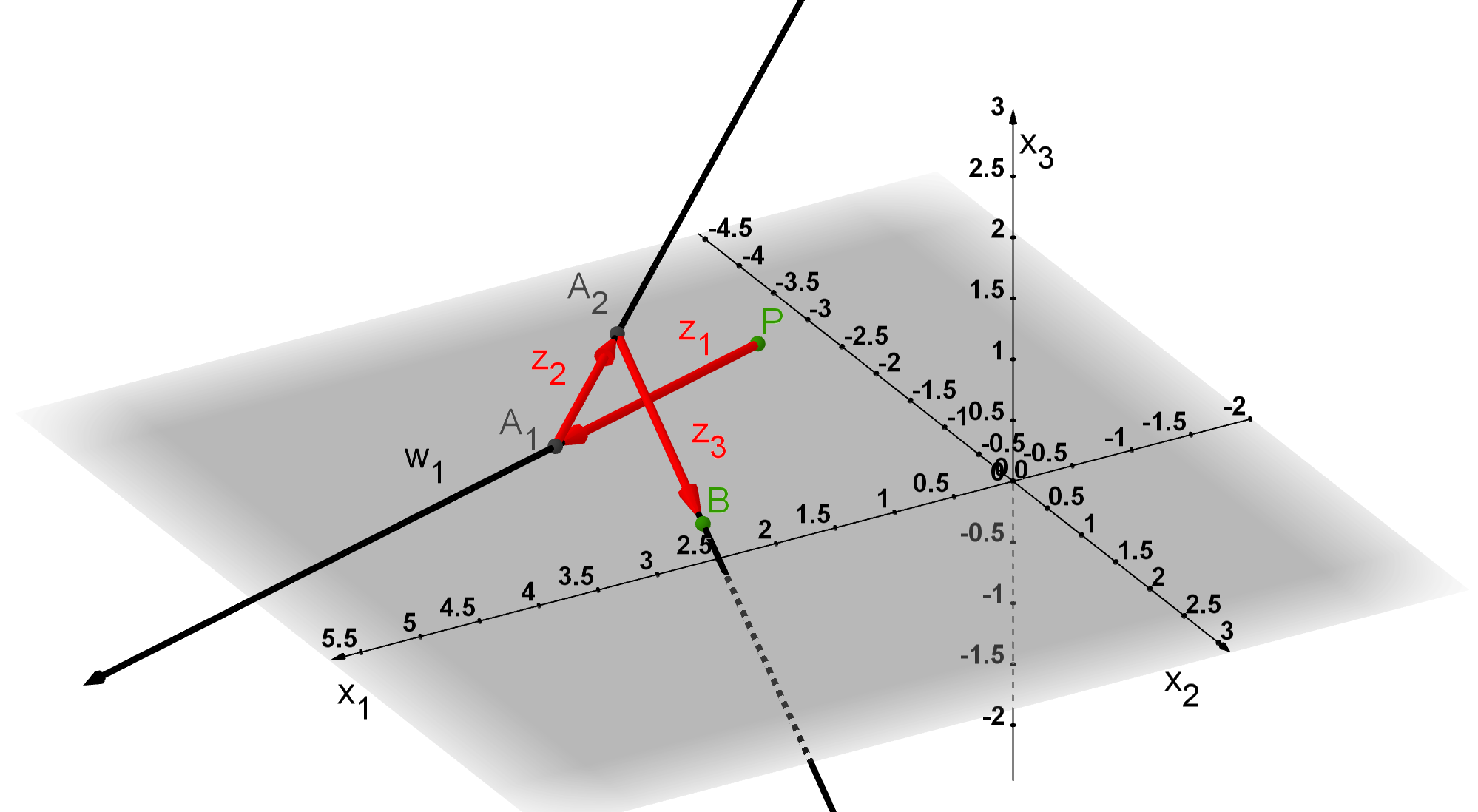
Stelle die durchlaufene Wanderung in einem geeigneten Koordinatensystem dar.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren
Vom Punkt P aus wird zuerst der Vektor $\vec z_1$ aus Aufgabe a) angehängt und an dessen Spitze dann noch die beiden anderen. am Schluss markiert man den Punkt B.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Da du in Teilaufgabe a) bereits die Vektoren berechnet hast, die du vom Punkt P aus durchläufst, musst du diese jetzt nur noch in ein Koordinatensystem malen.

Der zu berechnende Term

Länge der Wege berechnen

Wege verkürzen

Vektorkette bilden

Hast du eine Frage oder Feedback?

Schwierigkeit der Route

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?