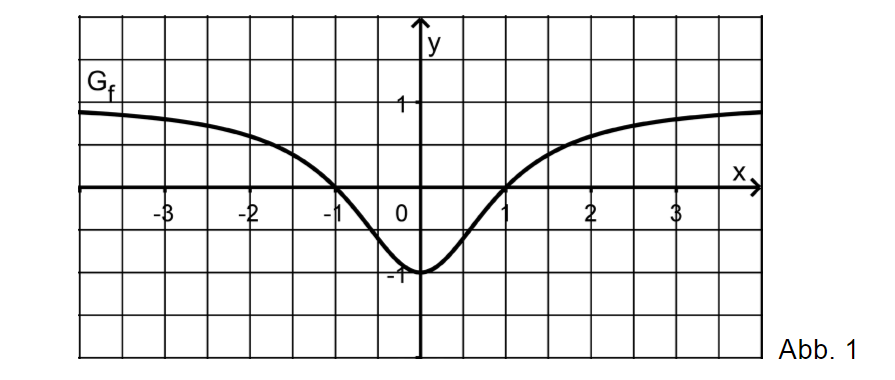
Teilaufgabe a)
Die vorgelegte Funktion ist eine gebrochen rationale Funktion, wobei Zählergrad gleich dem Nennergrad. Da der Nenner eine Summe nicht negativer Summanden ist und insgesamt immer positiv ist, ist die Funktion für alle reellen Zahlen definiert.
Zum Nachweis der Achsensymmetrie:
, für alle x
. Achsensymmetrisch.
Zum Verhalten im Unendlichen:
Man kürzt den Quotienten mit
Teilaufgabe b)
Zum Monotonieverhalten benutzt man die erste Ableitung. f ist eine gebrochen rationale Funktion, also kommt die Quotientenregel zur Anwendung.
.
Das Vorzeichen von wird nur vom Zähler bestimmt, da der Nenner als Quadrat keinen Vorzeichenwechsel hat.
Der Zähler wird graphisch durch die 1. Winkelhalbierende dargestellt. Also ergibt sich:
.
Teilaufgabe c)
Tangente an im Berührpunkt B(3;f(3)).
Die Tangente ist eine Gerade, daher: .
Die Steigung m ist der Wert der 1. Ableitung an der Stelle . .
Somit .
Die Koordinaten des Berührpunktes erfüllen die Tangentengleichung.
Man setzt die Koordinaten des Berührpunktes in die Tangentengleichung ein und erhält den y-Achsenabschnitt b.
Somit: t:
Winkelberechnung: