Überblick zum Satz des Pythagoras

1 Startseite

Ziel

Der Satz des Pythagoras ist den meisten, auch jüngeren Schülern vom Namen her schon bekannt. Allerdings wissen viele noch nicht, was mit der bekannten Formel $a^{2} + b^{2} = c^{2}$ genau gemeint ist. Das Ziel dieses Kurses ist nun, dass du die Funktion dieses Satzes verstehst und sicher damit umgehen kannst.

Voraussetzungen

Damit du diesen Kurs erfolgreich bearbeiten kannst, solltest du über rechtwinklige Dreiecke Bescheid wissen. Auch das Umformen von Gleichungen und das Rechnen mit Wurzeln sollte dir vertraut sein.

Was erwartet dich

Dir wird der Umgang mit dem Satz des Pythagoras mit einem Video und einer schriftlichen Erklärung, sowie mit Beispielen und Übungsaufgaben erklärt. Stellst du fest, dass dir ein Medium, also Video oder schriftliche Erklärung besonders liegt, kannst du dir auch nur dieses anschauen. Für den besten Lernerfolg, und gerade am Anfang, empfehlen wir jedoch, dass du dir beide Erklärungen anschaust.

Am Ende gibt es dann noch einen kurzen Test, an dem du überprüfen kannst, ob du alles verstanden hast.

2 Hypotenuse und Katheten

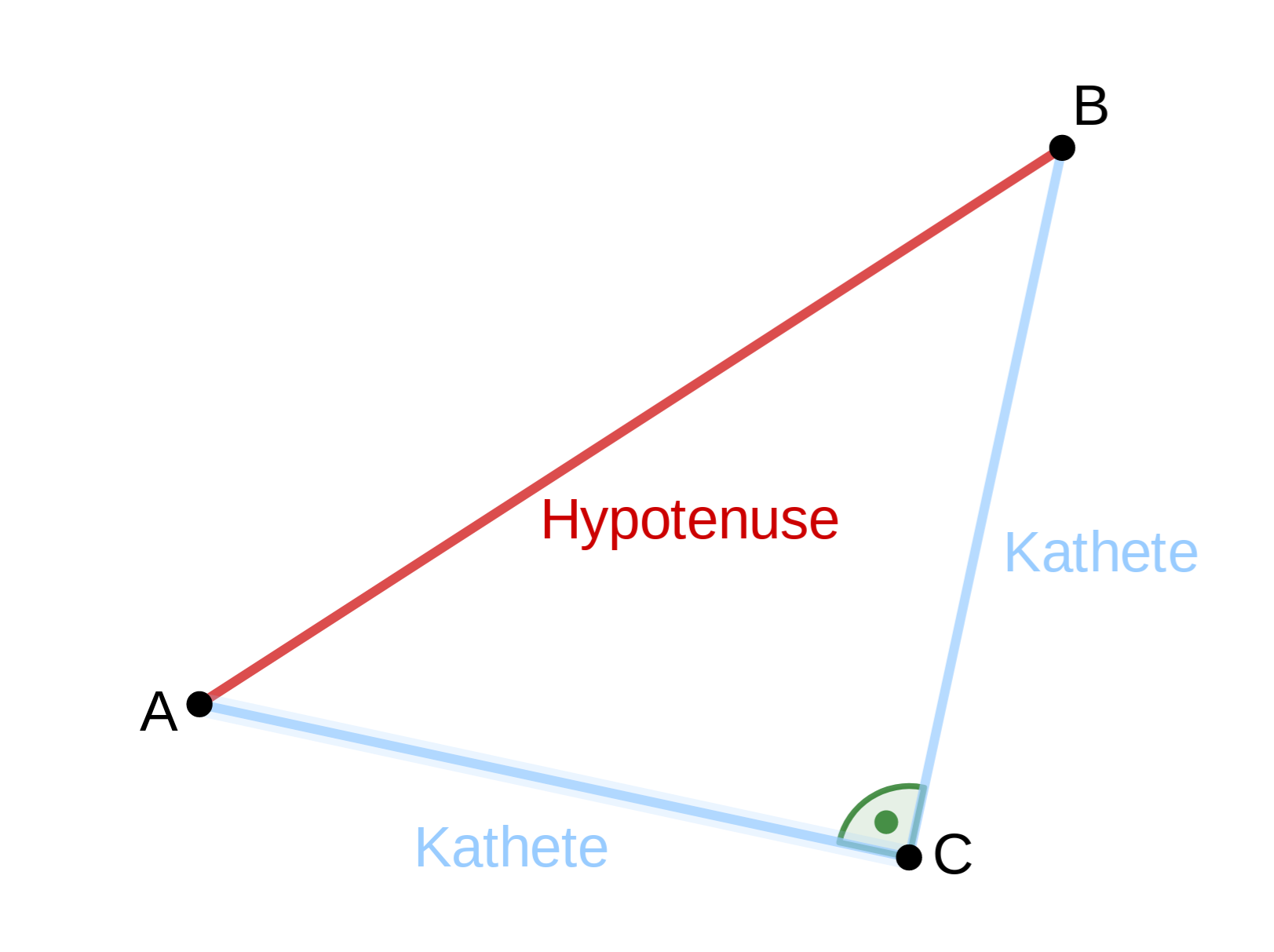
Die Hypotenuse

Die $\color{#Cc0000}{\mathrm{Hypotenuse}}$ ist die Seite, die dem rechten Winkel direkt gegenüberliegt.

Da in einem Dreieck die Winkelsumme 180° ist und somit der 90°-Winkel der größte in dem Dreieck ist, ist die ihm gegenüberliegende Hypotenuse auch die längste Strecke.

Die Katheten

Das sind die Seiten im Dreieck, zwischen denen der rechte Winkel liegt.

3 Video

In diesem Video wird dir gezeigt, was der Satz des Pythagoras aussagt und wie man mit ihm rechnet.

Laden

4 Der Satz des Pythagoras

Den Satz des Pythagoras kannst du nur bei einem rechtwinkligen Dreieck anwenden. Liegt ein solches Dreieck vor sagt der Satz des Pythagoras folgendes aus:

Merke

Bei einem rechtwinkligen Dreieck ist die Fläche des Quadrats über der Hypotenuse gleich der Summe der Quadratflächen über den Katheten.

Mit den Bezeichnungen aus der Figur ergibt sich damit die Formel:

\displaystyle a^2 + b^2 = c^2.

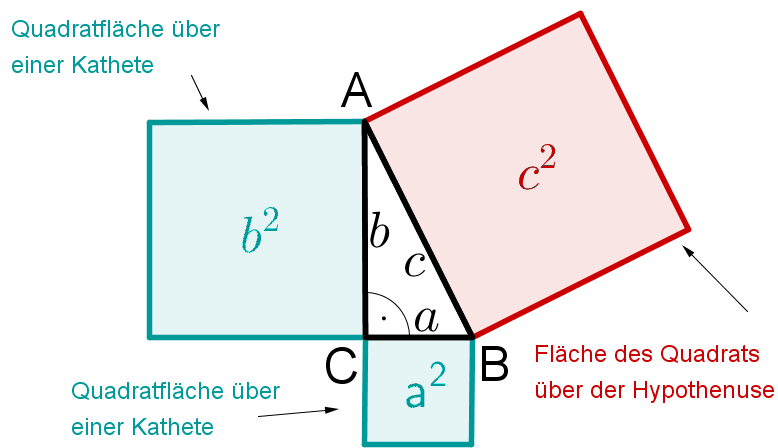
Wahrscheinlich erscheint dir der Satz des Pythagoras in seiner ausgeschriebenen Form, verglichen mit der sehr einfachen Formel, sehr kompliziert. Man muss ihn aber so formulieren, damit die Voraussetzung (man braucht ein rechtwinkliges Dreieck) mit angegeben wird und man von den Bezeichnungen der Seiten unabhängig ist. Dies wird in den folgenden zwei Beispielen deutlich:

Beispiel

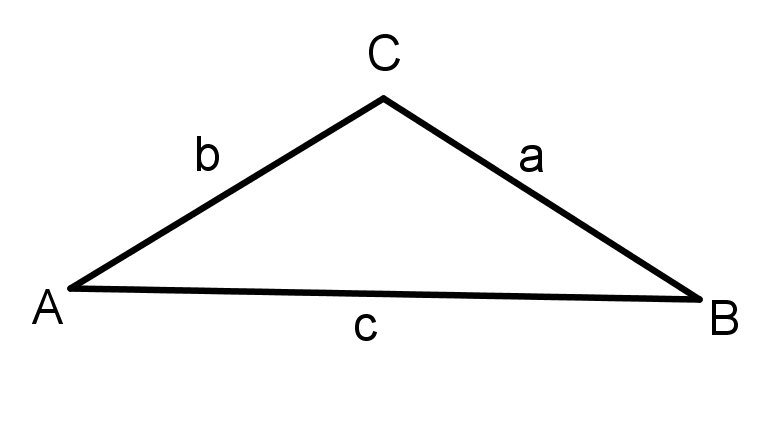
Die Formel stimmt hier nicht, da es sich um kein rechtwinkliges Dreieck handelt.

Beispiel

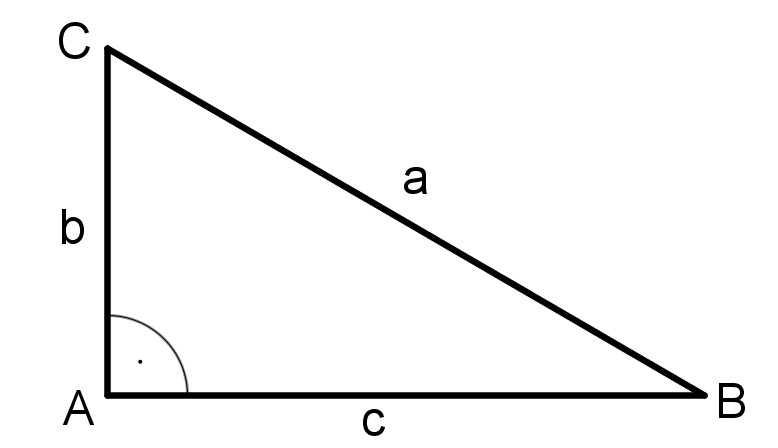
Auch hier stimmt die Formel $a^{2} + b^{2} = c^{2}$ nicht, denn die Hypotenuse in diesem Dreieck ist die Seite $a$ . Damit ist hier die korrekte Formel: $a^{2} = b^{2} + c^{2}$

Man muss also für die Anwendung des Satzes des Pythagoras beachten, wie die Seiten in dem rechtwinkligen Dreieck bezeichnet sind.

Wenn man den Satz des Pythagoras anwenden will, muss man also zuerst überprüfen,

ob ein rechtwinkliges Dreieck vorliegt und
wie die Seiten in dem Dreieck benannt sind.

und stellt dann fest,

welche Dreiecksseiten die Katheten sind und
welche die Hypotenuse ist.

Erst dann kann man die Formel richtig aufstellen.

5 Probier es selbst

Welche Seite ist die Hypotenuse in dem Dreieck?

Wie lautet dann der Satz des Pythagoras?

6 Beispielaufgaben

Gib, falls möglich, die allgemeine Formel vom Satz des Pythagoras an und berechne anschließend die fehlende Seite:

a)

Lösung

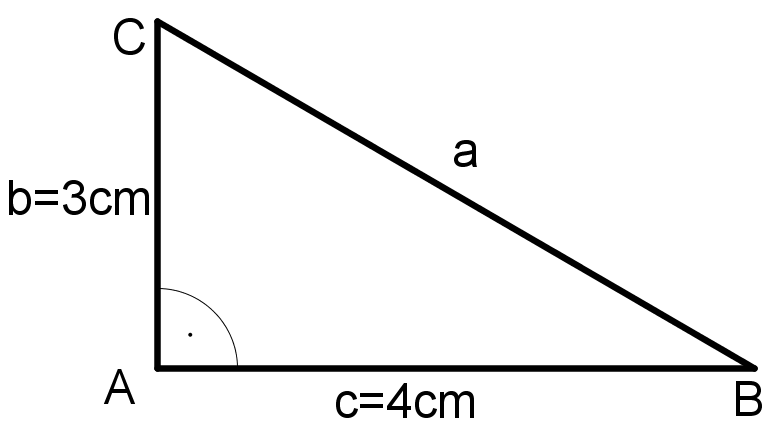
Das Dreieck $A B C$ ist ein rechtwinkliges Dreieck mit dem $90^\circ$ -Winkel bei $A$ . Deshalb ist die Seite $a$ die Hypotenuse (die Hypotenuse liegt immer dem rechten Winkel gegenüber) und die Seiten $b$ und $c$ sind in diesem Dreieck die Katheten.Damit ergibt sich nach dem Satz des Pythagoras folgende Formel:

\displaystyle a^2 = b^2 + c^2.

Nun setzt man die gegebenen Werte ein: $b = 3\, \mathrm{cm}$ und $c = 4\, \mathrm{cm}$ :

\displaystyle a^2 = (3\,\mathrm{cm})^2 + (4\,\mathrm{cm})^2 = 9\,\mathrm{cm}^2 + 16\, \mathrm{cm}^2 = 25\, \mathrm{cm}^2.

Durch Wurzelziehen auf beiden Seiten erhält man dann die Länge der Hypotenuse $a$ :

\displaystyle a^2 = 25\,\mathrm{cm}^2 \Leftrightarrow \sqrt{a^2} = \sqrt{25\, \mathrm{cm}^2} \Leftrightarrow a = 5\,\mathrm{cm}.

b)

Lösung

Das Dreieck $A B C$ ist kein rechtwinkliges Dreieck. Darum darf man hier den Satz des Pythagoras nicht anwenden!

c)

Lösung

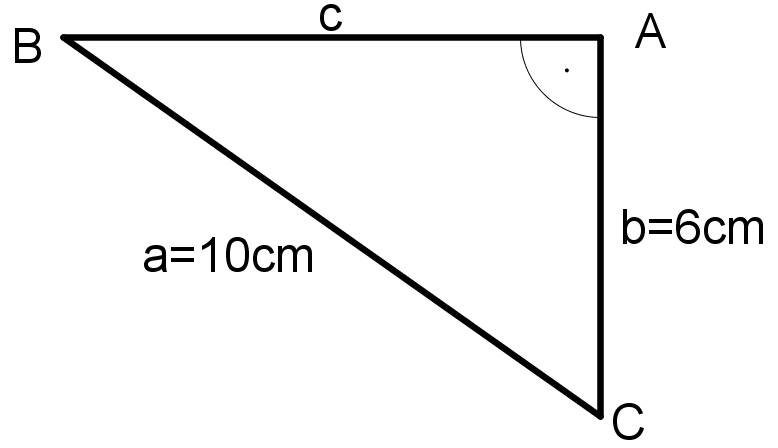
Das Dreieck $A B C$ ist ein rechtwinkliges Dreieck mit dem $90^\circ$ -Winkel bei $A$ . Deshalb ist die Seite $a$ die Hypotenuse (die Hypotenuse liegt immer dem rechten Winkel gegenüber) und die Seiten $b$ und $c$ sind in diesem Dreieck die Katheten.Damit ergibt sich nach dem Satz des Pythagoras folgende Formel:

\displaystyle a^2 = b^2 + c^2.

Gesucht ist aber die Länge der Kathete $c$ . Daher muss man die Formel nach $c$ auflösen:

$\displaystyle a^2$	$=$	$\displaystyle b^2+c^2$	$\displaystyle -b^2$
$\displaystyle a^2-b^2$	$=$	$\displaystyle c^2$	$\displaystyle \sqrt{\ }$
	↓	Ziehe die Wurzel. (Die negative Lösung $-\sqrt {a^2-b^2}$ bleibt bei Längen unberücksichtigt.)
$\displaystyle \sqrt{a^2-b^2}$	$=$	$\displaystyle \sqrt{c^2}$
$\displaystyle c$	$=$	$\displaystyle \sqrt{a^2-b^2}$

Nun muss man nur noch die Werte $a = 10\, \mathrm{cm}$ und $b = 6\, \mathrm{cm}$ einsetzen und ausrechnen:

$\displaystyle c$	$=$	$\displaystyle \sqrt{a^2-b^2}$
	$=$	$\displaystyle \sqrt{\left(10\text{cm}\right)^2-\left(6\text{cm}\right)^2}$
	$=$	$\displaystyle \sqrt{100\text{cm}^2-36\text{cm}^2}$
	$=$	$\displaystyle \sqrt{64\text{cm}^2}$
	$=$	$\displaystyle 8\$

7 Übungsaufgaben

Laden

8 Zusammenfassung

Beim Satz des Pythagoras muss man folgendes beachten:

Man kann den Satz nur bei einem rechtwinkligen Dreieck anwenden.
Die bekannte Formel $a^{2} + b^{2} = c^{2}$ ist nicht immer gültig, sondern nur wenn $c$ die Hypotenuse in dem Dreieck ist. Wenn eine andere Seite eine Hypotenuse ist, muss die Formel angepasst werden: $\left(\text{Kathete 1}\right)^2+\left(\text{Kathete 2}\right)^2=\ \text{Hypotenuse}^2$

Umkehrung des Satzes

Wenn man weiß, dass in einem Dreieck ABC die Gleichung $a^{2} + b^{2} = c^{2}$ gilt , dann liegt bei C ein rechter Winkel vor (und dann ist c die längste Seite und die Hypotenuse des Dreiecks).

9 Kann ich das?

Nun kannst du dich selber noch überprüfen. In diesem Kapitel stellen wir dir noch einmal Aufgaben. Löse diese und zähle die am Rand angegebenen Punkte zusammen, wenn du die Aufgabe richtig gelöst hast. Wenn du mindestens 8 von 10 Punkten erreicht hast, bist du in dem Thema fit.

Übung 1

Wann darf man den Satz des Pythagoras anwenden? (2 Punkte)

Übung 2

Wie lautet der Satz des Pythagoras bei diesem Dreieck? (2 Punkte)

Übung 3

Wann gilt die Formel $a^{2} + b^{2} = c^{2}$ ? (2 Punkte)

Übung 4

In einem Dreieck ist die Seite $a=3\,\mathrm{cm}$ und die Seite $b=4\,\mathrm{cm}$ lang. Wie lang muss die Seite $c$ sein, wenn diese die längste Seite in einem rechtwinkligen Dreieck sein soll? (2 Punkte)

Übung 5

Wie lang ist die fehlende Seite? (2 Punkte)

1 Startseite

Z﻿iel

Voraussetzungen

Was erwartet dich

2 Hypotenuse und Katheten

Die Hypotenuse

Die Katheten

3 Video

4 Der Satz des Pythagoras

5 Probier es selbst

6 Beispielaufgaben

7 Übungsaufgaben

8 Zusammenfassung

Umkehrung des Satzes

9 Kann ich das?

Übung 1

Übung 2

Übung 3

Übung 4

Übung 5

Ziel