Höhe des gleichseitigen Dreiecks

Mithilfe des Satzes des Pythagoras lässt sich die Formel für die Höhe eines gleichseitigen Dreiecks in Abhängigkeit der Seitenlänge a immer berechnen durch:

\displaystyle h=\frac{\sqrt{3}}{2}a

Berechnung der Höhe

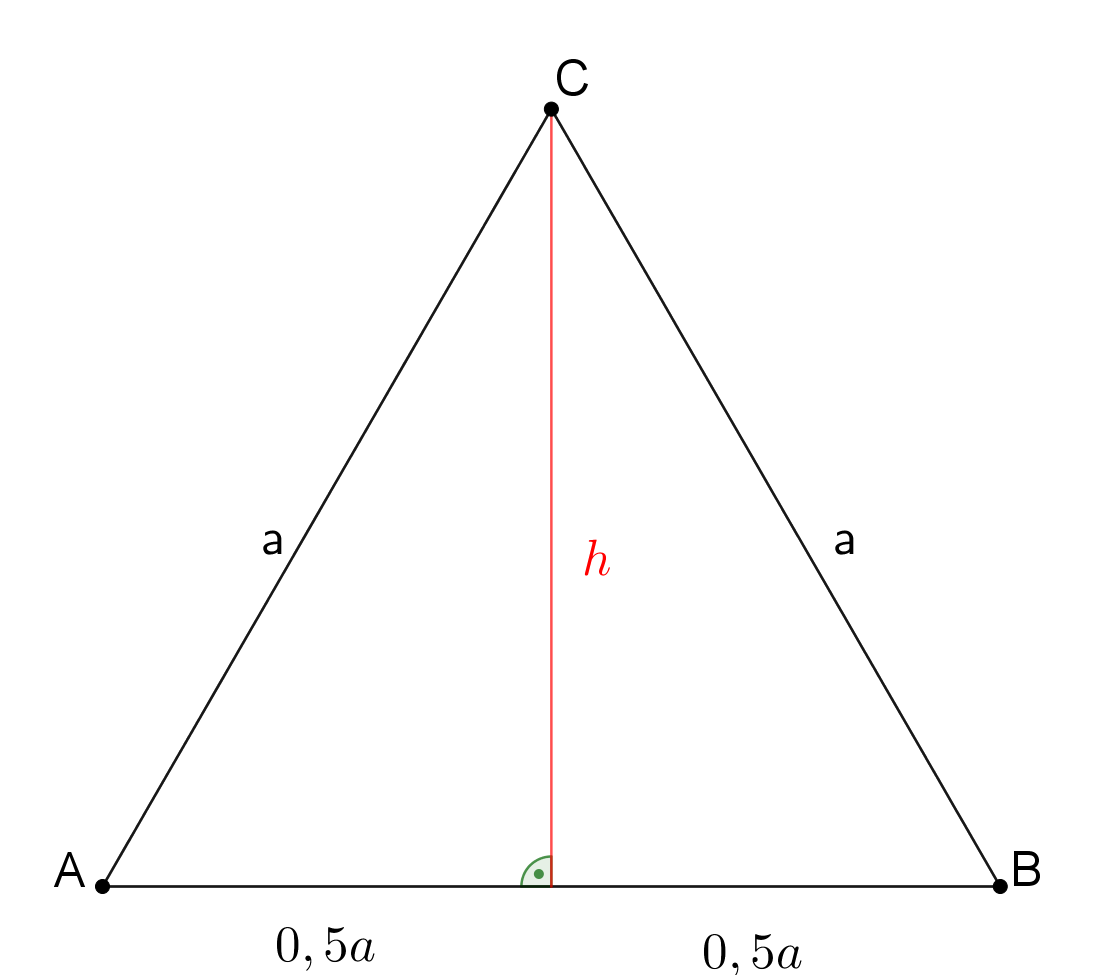
Da die Höhe gleichzeitig eine Symmetrieachse des Dreiecks ist und die Seite a somit in zwei gleich große Abschnitte teilt, sind beide Abschnitte 0,5a lang.

Das rechtwinklige Dreieck hat dann die Hypotenuse a und die Katheten h und 0,5a, also gilt mithilfe des Satz des Pythagoras:

$\left(\frac{1}{2}a\right)^2+h^2=a^2$

Diese Gleichung lässt sich nach h umformen:

$\displaystyle \left(\frac{1\ }{2}a\right)^2+h^2$	$=$	$\displaystyle a^2$
	↓	Berechne auf der linken Seite
$\displaystyle \frac{1}{4}a^2+h^2$	$=$	$\displaystyle a^2$	$\displaystyle -\frac{1}{4}a^2$
$\displaystyle h^2$	$=$	$\displaystyle \frac{3}{4}a^2$
	↓	Ziehe auf beiden Seiten die Wurzel. Da Seitenlängen positiv sind, musst du die negative Lösung nicht beachten.
$\displaystyle h$	$=$	$\displaystyle \sqrt{\frac{3}{4}}\cdot a$
	↓	Ziehe teilweise die Wurzel
$\displaystyle h$	$=$	$\displaystyle \frac{\sqrt{3}}{2}a$

Beispielaufgaben

Laden

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?