Zwei geometrische Figuren heißen zueinander ähnlich, wenn sie in ihrer Form exakt miteinander übereinstimmen. Eine ähnliche Figur kann verschoben, gedreht oder sogar gespiegelt sein.
Ihre Größe kann dabei verschieden sein, sodass eine ähnliche Figur um den Ähnlichkeitsfaktor vergrößert bzw. verkleinert wurde.
Sind Figuren ähnlich, wie in der Abbildung die Rechtecke oder Fünfecke so schreibe:
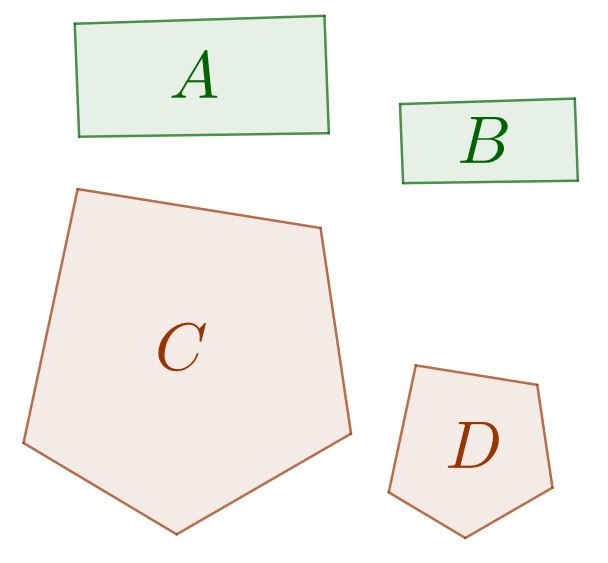
Ähnliche Figuren
Wir betrachten eine geometrische Figur. Eine zweite Figur ist zu dieser ähnlich, wenn sie aus einer, oder der Hinteraneinanderreihung folgender Prozesse (Abbildungen oder auch Transformationen genannt) hervorgeht:
Verschiebung aller Punkte um die gleiche Strecke. Diese Strecken müssen alle in dieselbe Richtung zeigen, also parallel sein.
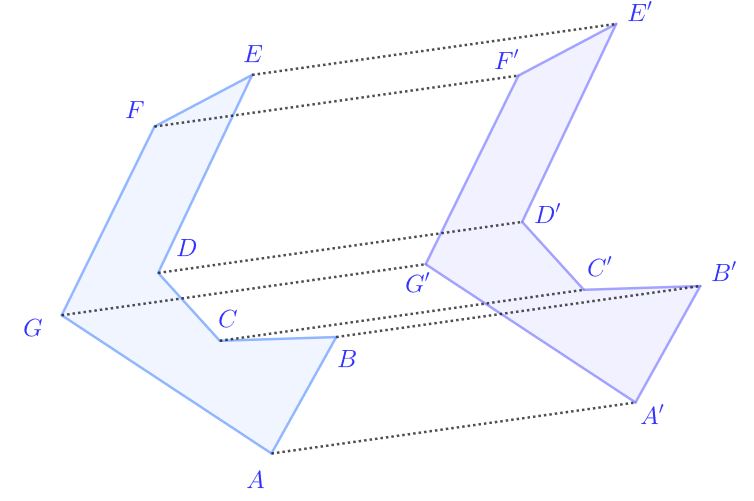
Drehung um einen Winkel .
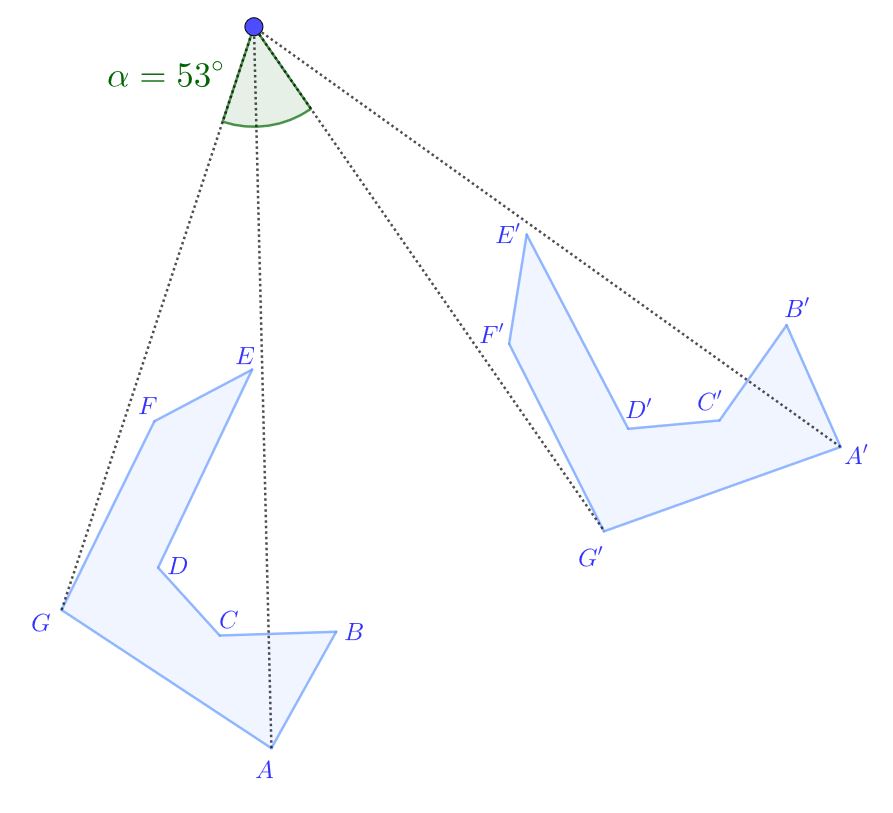
Spiegelung an einer Geraden. Hierbei wird jeder Punkt einzeln gespiegelt.
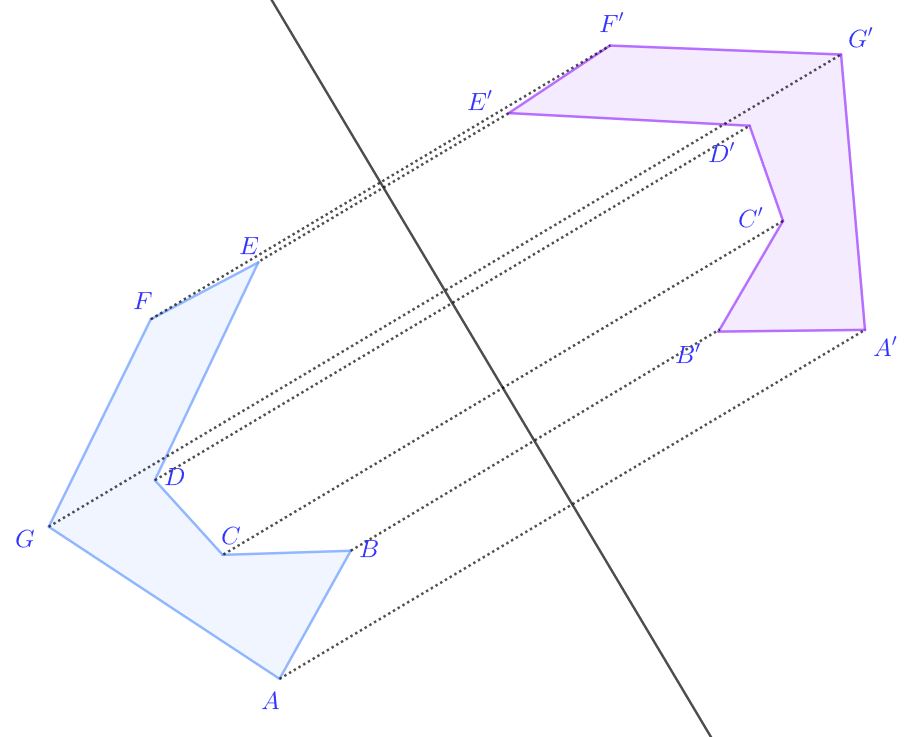
Vergrößerung bzw. Verkleinerung. Diese werden geometrisch durch die zentrische Streckung konstruiert.
Jede Seite der Figur wurde um den Ähnlichkeitsfaktor verkleinert.
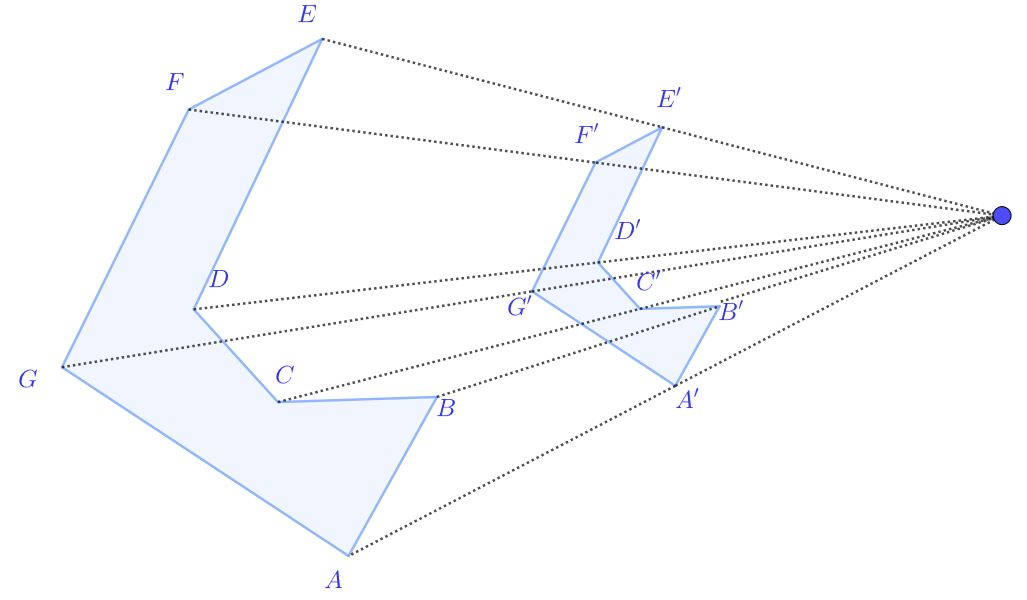
Ähnlichkeitsfaktor und dessen Berechnung
Der Ähnlichkeitsfaktor oder Ähnlichkeitsmaßstab gibt den Faktor der Vergrößerung bzw. Verkleinerung an.
Wird eine Figur um das Doppelte vergrößert, ergibt sich der Maßstab .
Wird eine Figur auf ein Drittel seiner Größe verkleinert, beträgt .
Ähnlichkeitsfaktor berechnen
Sind zwei ähnliche Figuren und gegeben, so stehen alle ihre Seiten im Verhältnis des Ähnlichkeitsfaktors .
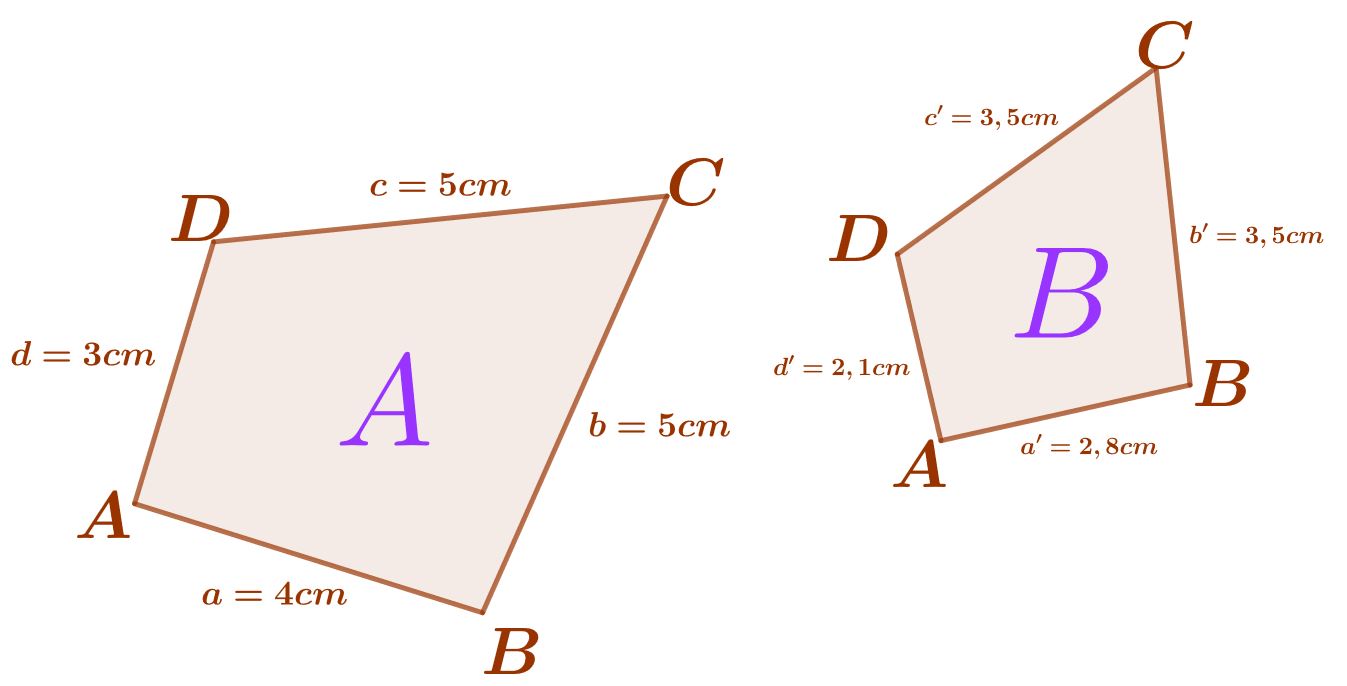
Daher reicht es aus, zwei Seiten, bspw. auszuwählen und diesen zu bestimmen:
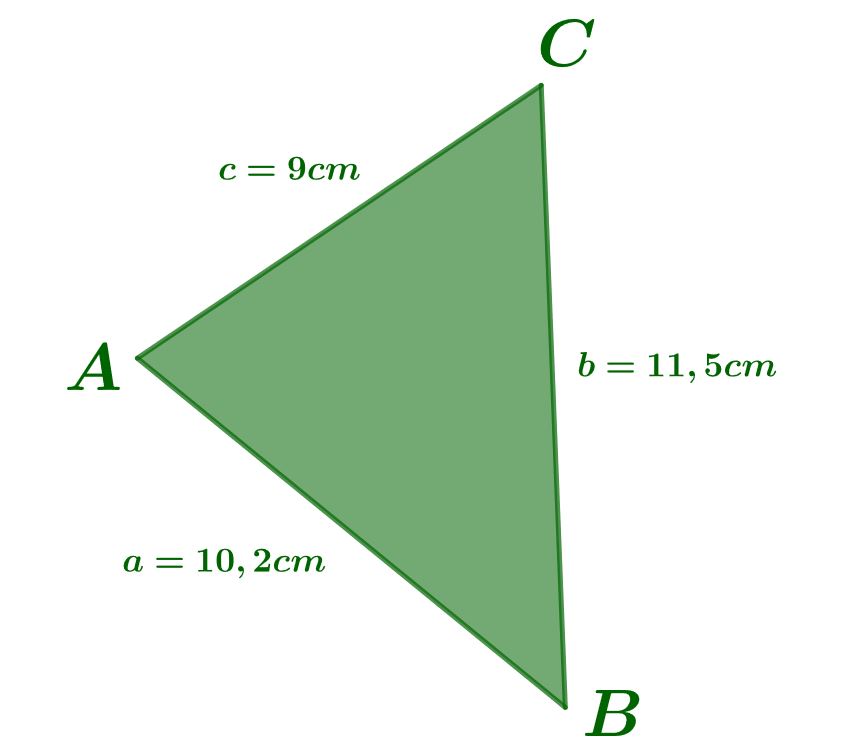
Seitenlängen berechnen bei gegebenem Ähnlichkeitsfaktor
Aus dem nebenstehenden Dreieck soll eine ähnliche Figur konstruiert werden, welche um den Ähnlichkeitsfaktor vergrößert wurde.
Die neuen Seitenlängen betragen nun:
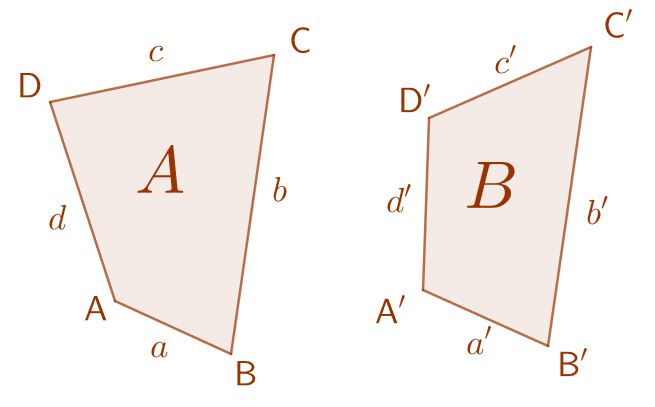
Fehlvorstellung: Gleiche Form
Das Wort Ähnlichkeit in unserem Sprachgebrauch führt zu einer anderen Vorstellung, wie sie in der Mathematik gemeint ist.
Diese Vierecke haben in etwa die gleiche Form, sind im mathematischen Sinne aber nicht ähnlich, denn für ihre Seiten gilt:
Somit sind sie nicht ähnlich, schreibe .
Zusammenhang zwischen Ähnlichkeit und Kongruenz
Kongruente Dreiecke sind durch Verschiebung, Drehung und Spiegelung ineinander überführbar. Ähnliche Dreiecke sind zusätzlich mit einer Vergrößerung/Verkleinerung zu erhalten, was Ähnlichkeit als Konzept etwas allgemeiner macht als Kongruenz. Deshalb gilt auch:
Applet: Ähnliche Figur durch Vergrößerung/Verkleinerung
Durch die zentrische Streckung wird eine Figur in einem Maßstab vergrößert/verkleinert. Diese Figur ist ähnlich zur ursprünglichen Figur. Verwende den Schieberegler für um diese Figur zu skalieren.
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu Kongruenz und Ähnlichkeit von Dreiecken
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
