Gegeben sind die folgenden Funktionsgraphen:
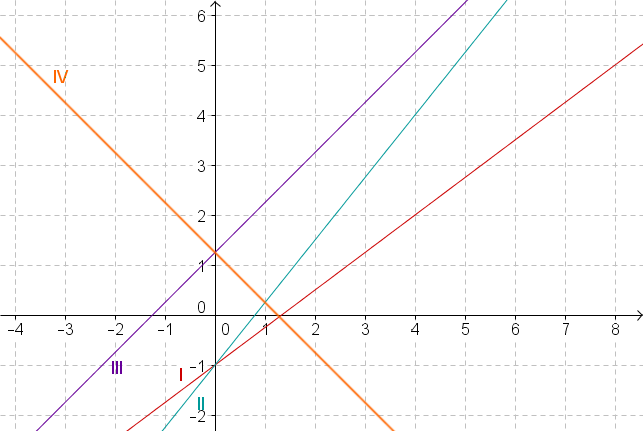
Welcher der vier Graphen gehört zur Gleichung
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichungen
Vorgegebene Graphengleichung:
Du kannst die Steigung und den y-Achsenabschnitt dieses Graphen an der Gleichung ablesen.
Überprüfe zuerst bei welchen Funktionen der y-Achsenabschnitt beträgt, indem du den y-Wert jedes Graphen abliest, indem die y-Achse geschnitten wird.
Nur Graph I und II haben den y-Achsenabschnitt also kannst du jeden anderen Graphen ausschließen.
Überprüfe nun welcher der beiden Graphen die Steigung besitzt, indem du vom Punkt ausgehend eins nach rechts gehst und überprüfst, welcher der beiden y-Werte sich um erhöht.
Beide Graphen beginnen beim Punkt . Da die gesuchte Gerade die Steigung hat, geht sie auch durch den Punkt .
Durch diesen Punkt läuft nur die Gerade II.
Der Graph II ist der Graph, der zu der vorgegebenen Gleichung gehört.
Hast du eine Frage oder Feedback?
Wie lautet die Gleichung zum Graphen III?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichungen
zu überprüfende Gerade: Graph III
Lies zuerst wo der Graph die y-Achse schneidet, um den y-Achsenabschnitt zu ermitteln.
Der y-Wert des Punktes, indem die y-Achse geschnitten wird, beträgt . Somit ist .
Lies nun ab um wieviel sich der y-Wert verändert, wenn du ausgehend von , eins nach rechts gehst. Dadurch ermittelst du die Steigung.
Der y-Wert erhöht sich von auf . Somit beträgt die Steigung .
Stelle die Gleichung auf.
⇒ Der Graph III hat die Gleichung
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
