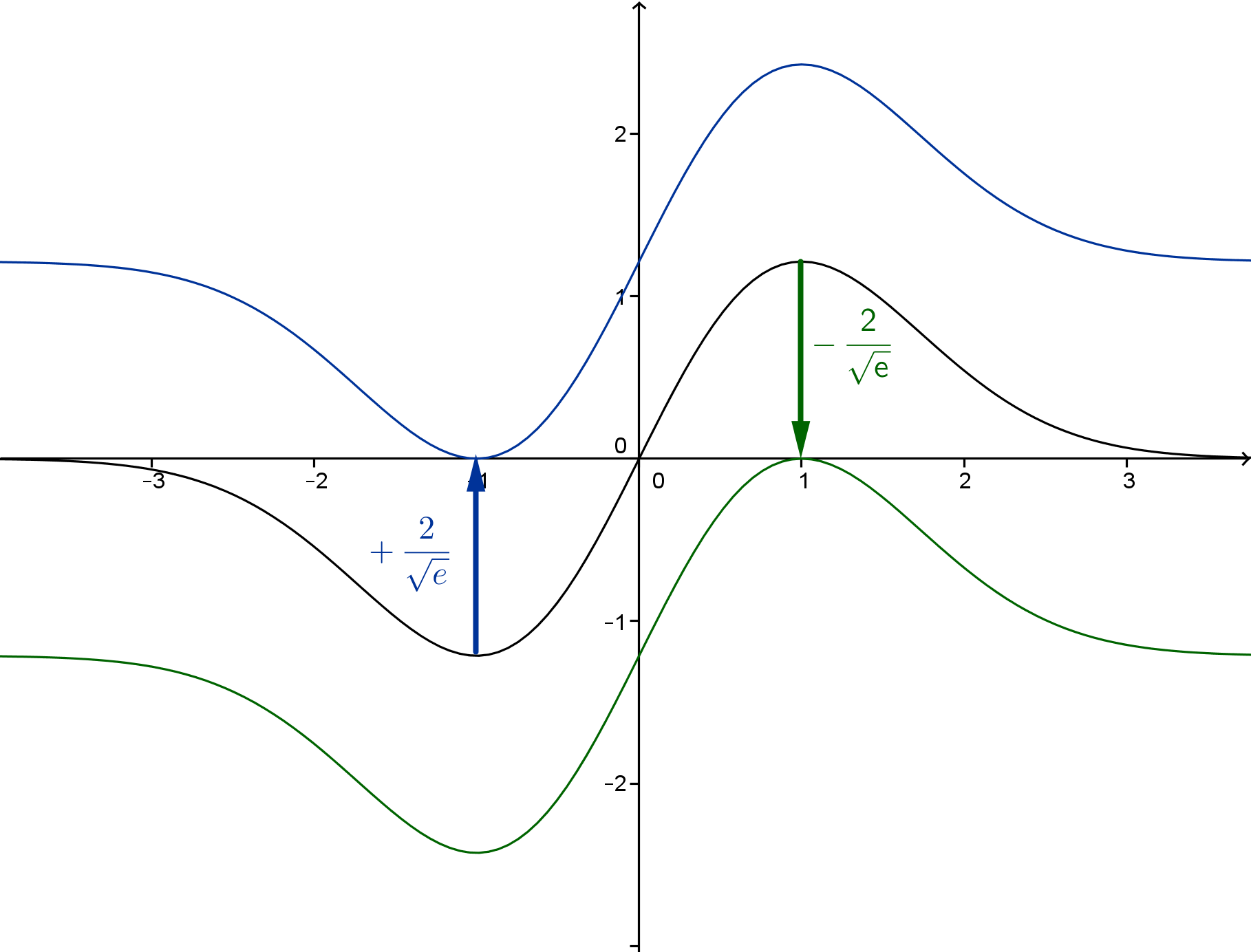
Im Folgenden wird die Schar der definierten Funktionen mit betrachtet.
Geben Sie in Abhängigkeit von c ohne weitere Rechnung die Koordinaten des Hochpunkts des Graphen von sowie das Verhalten von für
an.
Die Anzahl der Nullstellen von hängt von ab. Geben Sie jeweils einen möglichen Wert von an, sodass gilt:
a.) hat keine Nullstelle.
b.) hat genau eine Nullstelle.
c.) hat genau zwei Nullstellen.
Begründen Sie für anhand einer geeigneten Skizze, dass
gilt.