In diesem Artikel lernst du, wie du mit dem Dreisatz indirekte Proportionalitäten berechnen kannst.
Der Dreisatz ist ein Verfahren, um aus drei gegebenen Werten, die miteinander im Verhältnis stehen bzw. indirekt proportional sind, den unbekannten vierten Wert zu berechnen. Vielleicht kennst Du die indirekte Proportionalität auch als Anti-Proportionalität.
Zum Beispiel:
Ihr seid 2 Freundinnen und benötigt 6 Stunden, um Tischdeko zu basteln.
Wie lange braucht Ihr, wenn Euch noch eine Freundin hilft?

Ergebnis: Wenn Ihr zu Dritt an der Deko bastelt, braucht Ihr nur 4 Stunden.
Je mehr Personen mithelfen, desto weniger Zeit wird gebraucht.
Je weniger Personen mithelfen, desto mehr Zeit wird gebraucht.
Nochmal ausführlich erklärt:
Grundstruktur:
Du hast immer eine Grundgröße und eine zugeordnete Größe, die zueinander im Verhältnis stehen bzw. indirekt proportional sind. z.B. seid Ihr 2 Freundinnen (Grundgröße), die 6 Stunden Bastelzeit für Deko (zugeordnete Größe) brauchen.
Gesucht wird nach dem zugeordneten Wert einer neuen Grundgröße. z.B. Wenn 3 Freundinnen (neue Grundgröße) basteln und sich fragen, wie lange sie dann für die gleiche Menge Deko benötigen.
Der gesuchte Wert – die neue zugeordnete Größe- wird mit dem Dreisatz berechnet. z.B. Wie lange brauchen 3 Freundinnen?
Berechnung des Dreisatzes:
Folgende Fragen stellst Du Dir vorab:
1) Was ist die Grundgröße?
Die Anzahl der Freundinnen – also 2.
2) Was ist die zugeordnete Größe?
Die Zeit in Stunden, die Ihr benötigt – also 6 Stunden.
3) Was ist die neue Grundgröße?
Die Anzahl der Freundinnen inkl. der neu dazugekommenen, also 3.
4) Was wird gesucht?
Die Zeit in Stunden für die neue Grundgröße, also die 3 Personen.
5) Handelt es sich hierbei um eine direkte oder indirekte
Proportionalität?
Um eine indirekte Proportionalität, denn die Grundgröße (Anzahl
Freundinnen) und die zugeordnete Größe (Kosten der Fahrkarte) steigen bzw.
fallen entgegengesetzt.
Mehr Personen benötigen weniger Zeit.
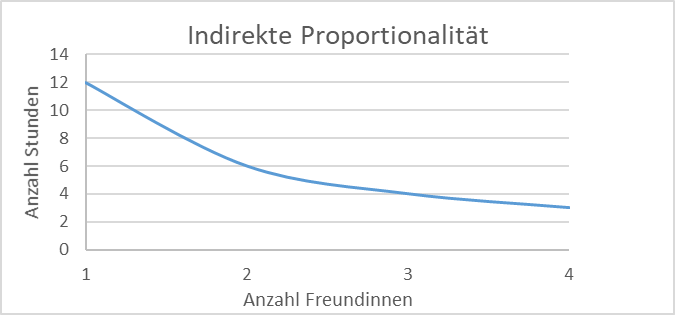
Bei der indirekten Proportionalität gilt:
Je mehr der Wert der Grundgröße wird, desto weniger wird auch der Wert der zugeordneten Größe.
Je weniger der Wert der Grundgröße wird, desto mehr wird der Wert der zugeordneten Größe.
Diese Schritte führst Du als nächstes durch:
1) Setze die Zahlen ins Verhältnis:
[Verwende dafür ein "entspricht"-Zeichen ("")]
Die Grundgrößen mit den bekannten Zahlen stehen dabei wieder links, die zugeordnete Größe und der gesuchte Wert rechts.
2) Berechne, wie viel Zeit in Stunden für 1 Person benötigen wird:

Dividiere hierfür die Grundgröße mit der Grundgröße und multipliziere die zugeordnete Größe mit der Grundgröße.
3) Berechne, wie viel Zeit in Stunden die neue Grundgröße, also 3
Personen, benötigen würden:

Multipliziere hierfür die 1 Person mit der neuen Grundgröße und dividiere die zugeordnete Größe für 1 Person mit der neuen Grundgröße.
Ergebnis: Mit 3 Personen lassen sich die Tischdekoration in nur 4 Stunden basteln.
Allgemein gesagt:
a= Grundgröße
b= zugeordnete Größe
c= neue Grundgröße
Teile die linke Seite durch a
Multipliziere die rechte Seite mit a
Multipliziere die linke Seite mit c
Teile die rechte Seite mit c
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Gemischte Aufgaben zu Proportionalität und Dreisatz
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
