Man kann Strecken relativ leicht mithilfe der zentrischen Streckung teilen.
Eine typische Aufgabenstellung könnte zum Beispiel lauten:
Teile die Strecke im Verhältnis .
Oder allgemeiner: Teile die Stecke im Verhältnis .
Was bedeutet "Teile im Verhältnis a:b"?
Wenn man eine Strecke im Verhältnis teilen will, dann möchte man einen Punkt finden für den gilt:
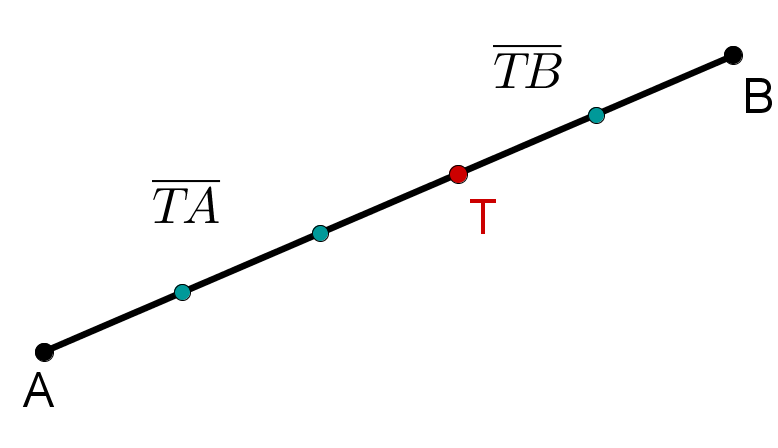
Das bedeutet nicht zwangsläufig, dass und/oder gilt. Man betrachtet hier nur ein Verhältnis!
Vorgehen
Um eine solche Aufteilung zu erhalten, zerlegt man die Strecke in Teilstücke. Für die Strecken und folgt dann:
, sowie
Das bedeutet also in Worten:
Wenn man eine Strecke im Verhältnis teilen will, versucht man die Strecke in Teile aufzuteilen. Dann besteht die erste Teilstrecke aus solchen Teilen und die zweite Teilstrecke aus solchen Teilen.
Beispiel
Die Strecke soll im Verhältnis geteilt werden. Wie lang ist dann die Strecke von Punkt zum Teilpunkt ?
Lösung: Gesucht ist die Länge der Strecke :
Alternative Herangehensweise:
Man teilt die Strecke in Teile auf, also in Teile à . Die Teilstrecke besteht dann aus solchen Teilen, ist also mal lang. Also .
Geometrische Konstruktion einer Streckenteilung
Die Strecke soll im Verhältnis geteilt werden. (Im Applet ist das Verhältnis )
Zeichne eine Gerade durch .
Zeichne einen Kreis um , mit irgendeinem Radius .
Zeichne einen weiteren Kreis mit demselben Radius, dessen Mittelpunkt der Schnittpunkt des vorherigen Kreises mit der Geraden ist.
Wiederhole dies mal.
Verbinde den letzten Schnittpunkt mit dem Punkt .
Zeichne zu der gerade gezeichneten Geraden eine Parallele durch den -ten Schnittpunkt.
Der Schnittpunkt S dieser Parallelen mit teilt die Strecke im Verhältnis .
Im Applet kann man sich die Schritte mithilfe des Schiebereglers anzeigen lassen.
Übungsaufgaben
Laden
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
