Stelle zunächst die Gerade $AB$ auf. Die allgemeine Geradengleichung in der analystischen Geometrie lässt sich schreiben als

Dabei ist $\overrightarrow{p}$ der Ortsvektor und $\overrightarrow{u}$ der Richtungsvektor der Geraden.

Bestimme den Richtungsvektor der Geradengleichung, also $\overrightarrow{AB}$ ($\overrightarrow{BA}$ funktioniert auch).

$\overrightarrow{AB} = \overrightarrow{B} - \overrightarrow{A} =\begin{pmatrix}6\\1\\-12\end{pmatrix} - \begin{pmatrix}2\\1\\-4\end{pmatrix}=\begin{pmatrix}4\\0\\-8\end{pmatrix}$

Als Ortsvektor der Geradengleichung kannst du $\overrightarrow{A}$ oder $\overrightarrow{B}$ nehmen (hier wird $\overrightarrow{A}$ verwendet). Du erhältst dann die folgende Geradengleichung:

Setze jetzt den Ortsvektor des Punkts $C$ für $\overrightarrow{x}$ ein, um zu prüfen, ob $C$ auf der Geraden liegt:

Jetzt erhältst du die folgenden drei Gleichungen, die du nach $\lambda$ auflösen kannst:

$-2=\lambda\cdot 4\Longrightarrow\lambda=-\frac{1}{2}$

$0=\lambda\cdot 0$

$4=\lambda\cdot(-8)\Longrightarrow\lambda=-\frac{1}{2}$

Die drei Gleichungen sind für $\lambda=-\frac{1}{2}$ erfüllt und somit liegt $C$ auf der Geraden $AB$.

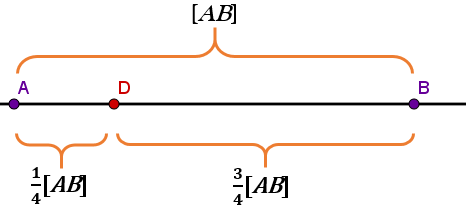
Setzt man nun $A$ und $B$ in die Geradengleichung ein, stellt man fest, dass für $A$ $\lambda=0$ und für $B$ $\lambda=1$.Es liegen also nur Punkte mit $\lambda\in[0;1]$ auf der Strecke $[AB]$. Da für $C$ $\lambda=-\frac{1}{2}$, liegt $C$ nicht auf der Strecke $[AB]$.

Du kannst zunächst zur Veranschaulichung eine Skizze wie die nebenstehende zeichnen. Aus Teilaufgabe a) weißt du schon, dass für den Punkt $A$ auf der Geraden $AB$ $\lambda=0$ und für $B$ $\lambda=1$. Da $D$ dreimal so weit von $B$ entfernt ist wie von $A$, ist für den Punkt $D$ $\lambda=\frac{1}{4}$.

Setze $\lambda=\frac{1}{4}$ in die Geradengleichung $AB$ ein, um $\overrightarrow{D}$ zu erhalten:

$\Longrightarrow$ $D$ hat die Koordinaten $(3|1|-6)$.