Geometrie, Teil A, Aufgabengruppe 1
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
Gegeben sind die Punkte , und .
Weisen Sie nach, dass der Punkt auf der Geraden , nicht aber auf der Strecke liegt. (3 BE)
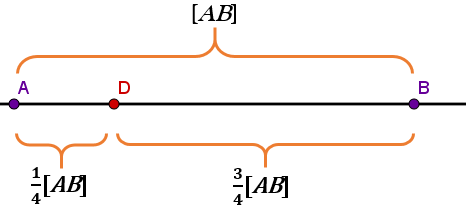
Auf der Strecke gibt es einen Punkt , der von dreimal so weit entfernt ist wie von . Bestimmen Sie die Koordinaten von . (2 BE)
- 2
Gegeben ist die Ebene .
Der Schnittpunkt von mit der -Achse, der Schnittpunkt von mit der -Achse und der Koordinatenursprung sind die Eckpunkte eines Dreiecks. Bestimmen Sie den Flächeninhalt dieses Dreiecks. (2 BE)
Ermitteln Sie die Koordinaten des Vektors, der sowohl ein Normalenvektor von als auch der Ortsvektor eines Punktes der Ebene ist. (3 BE)
- 3
Gegeben ist die Ebene .
Der Schnittpunkt von mit der -Achse, der Schnittpunkt von mit der -Achse und der Koordinatenursprung sind die Eckpunkte eines Dreiecks. Bestimmen Sie den Flächeninhalt dieses Dreiecks. (2 BE)
Ermitteln Sie die Koordinaten des Vektors, der sowohl ein Normalenvektor von als auch der Ortsvektor eines Punktes der Ebene ist. (3 BE)
- 4
Gegeben sind die Punkte , und .
Weisen Sie nach, dass der Punkt auf der Geraden , nicht aber auf der Strecke liegt. (3 BE)
Auf der Strecke gibt es einen Punkt , der von dreimal so weit entfernt ist wie von . Bestimmen Sie die Koordinaten von . (2 BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?