Drei konventionelle landwirtschaftliche Betriebe und sind untereinander und mit dem Markt nach dem Leontief – Modell verflochten. Das Diagramm stellt die momentane Verflechtung der Betriebe in Mengenein-heiten dar, mit .
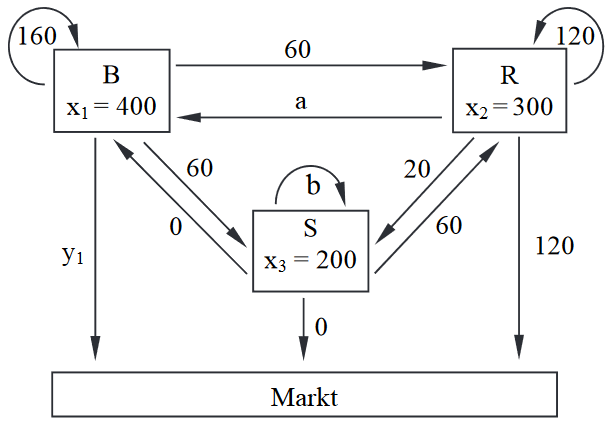
Bestimmen Sie , und und geben Sie deren Bedeutung im Sachzusammenhang an. Berechnen Sie die Inputmatrix . (6 BE)
In der nächsten Produktionsperiode wird erwartet, dass die Nachfrage von Produkten der Betriebe auf und auf sinkt. Betrieb soll an den Markt liefern. Berechnen Sie den zugehörigen Produktionsvektor. Nennen Sie die Ursache dafür, dass trotz des Absinkens der Produktion in allen drei Betrieben die Marktabgabe in einem Betrieb steigt. (7 BE)
Die Betriebe entschließen sich mittelfristig auf biologische Betriebsführung umzustellen. Für die Umstellungszeit ergibt sich die neue Inputmatrix
Dabei ist ein technologieabhängiger Parameter. Berechnen Sie, für welchen Wert von die Summe der Marktabgaben aller drei Betriebe am größten ist, wenn der Produktionsvektor geplant ist.
Hinweis: Es kann davon ausgegangen werden, dass die Marktabgaben der drei Betriebe für nicht negativ sind. (8 BE)
