B II

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Im $ℝ^{3}$ sind die Punkte $A (2 | 2 | 2), P (2 | – 3 | 5)$ und die Ebene
$E : \vec{x} = (\begin{array}{c} 2 \\ 2 \\ 2 \end{array}) + r \cdot (\begin{array}{c} 2 \\ 0 \\ 0 \end{array}) + s \cdot (\begin{array}{c} 2 \\ 1 \\ 0 \end{array})$ mit $r, s \in ℝ$ gegeben.
1. Zeigen Sie, dass die beiden Richtungsvektoren $\vec{u}$ und $\vec{v}$ der Ebene $E$ zusammen mit dem Vektor $\vec{A P}$ eine Basis des $ℝ^{3}$ bilden. Begründen Sie, dass der Punkt $P$ nicht Element der Ebene $E$ ist. (5 BE)
2. Ermitteln Sie eine Koordinatengleichung der Ebene $E$ und geben Sie die besondere Lage von $E$ im Koordinatensystem an. (3 BE)
3. Ermitteln Sie eine Gleichung der Schnittgeraden $s$ der Ebenen $E$ und $F : x_{1} + x_{3} = 0$ . (3 BE)
4. Zeigen Sie, dass $A \notin s$ gilt. Entscheiden Sie ohne weitere Rechnung, wie die Schnittgerade $s$ zur Geraden $A P$ liegt. Fertigen Sie hierzu eine aussagekräftige Skizze an. (4 BE)
5. Untersuchen Sie die gegenseitige Lage der Geradenschar
  $g_{a} : \vec{x} = (\begin{array}{c} 2 a \\ 2 \\ a \end{array}) + μ \cdot (\begin{array}{c} - 1 \\ 2 \\ - 2 a \end{array})$ mit $a, μ \in ℝ$ und der Ebene $E$ in Abhängigkeit von $a$ . (4 BE)
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
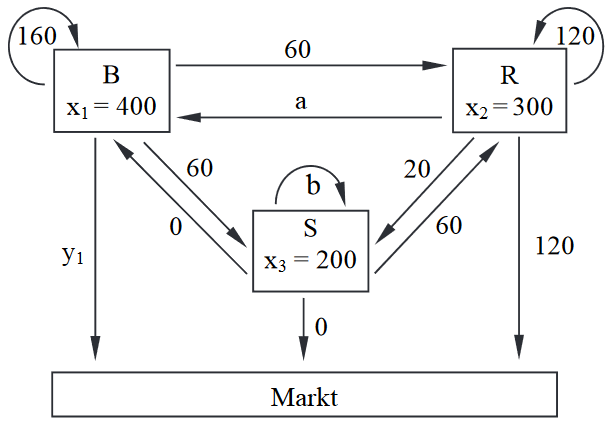
Drei konventionelle landwirtschaftliche Betriebe $B, R$ und $S$ sind untereinander und mit dem Markt nach dem Leontief – Modell verflochten. Das Diagramm stellt die momentane Verflechtung der Betriebe in Mengenein-heiten $M E$ dar, mit $a, b, y_{1} \in ℝ^{+}$ .
1. Bestimmen Sie $a$ , $b$ und $y$ und geben Sie deren Bedeutung im Sachzusammenhang an. Berechnen Sie die Inputmatrix $A$ . (6 BE)
  
  Berechnung der Parameter a, b und $y_{1}$
  Werte des Verflechtungsdiagramms in eine Input-Output Tabelle eintragen:
  B
  R
  S
  Markt
  Produktion
  B
  160
  60
  60
  $y_{1}$
  400
  R
  a
  120
  20
  120
  300
  S
  0
  60
  b
  0
  200
  Aus den Zeilen der Tabelle erhält man folgende Gleichungen:
  $160 + 60 + 60 + y_{1}$ $=$ $400$
  ↓
  nach $y_{1}$ umformen
  $y_{1}$ $=$ $400 - 160 - 60 - 60 = 120$
  $a + 120 + 20 + 120$ $=$ $300$
  ↓
  nach a umformen
  $a$ $=$ $300 - 120 - 20 - 120 = 40$
  $60 + b$ $=$ $200$
  ↓
  nach b umformen
  $b$ $=$ $200 - 60 = 140$
  Die gesuchten Parameter sind $a = 40, b = 140, y_{1} = 120$ .
  Bedeutung im Sachzusammenhang
  $a = 40$ bedeutet, dass Betrieb R 40 ME an Betrieb B liefert.
  $b = 140$ bedeutet, dass Betrieb S 140 ME seiner Produktion für den Eigenbedarf verwendet.
  $y_{1} = 120$ bedeutet, dass Betrieb B 120 ME an den Markt liefert.
  Berechnung der Inputmatrix A
  Die Koordinaten der Matrix A ergeben sich, indem man die Zahlenwerte der Input-Output-Tabelle durch die entsprechenden Werte des Produktionsvektors teilt.
  $a_{\begin{array}{c} i j \end{array}} = \frac{Input, den Sektor j von Sektor i erhält}{Gesamtproduktionsmenge im Sektor i}$
  $A = (\begin{array}{ccc} \frac{160}{400} & \frac{60}{300} & \frac{60}{200} \\ \frac{40}{400} & \frac{120}{300} & \frac{20}{200} \\ \frac{0}{400} & \frac{60}{300} & \frac{140}{200} \end{array})$ $\Rightarrow A = (\begin{array}{ccc} 0,4 & 0,2 & 0,3 \\ 0,1 & 0,4 & 0,1 \\ 0 & 0,2 & 0,7 \end{array})$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Übertrage Werte in eine Input-Output-Tabelle.
  Bestimme Parameter a, b und $y_{1}$ mittels Zeilenoperationen.
  Bestimme Koordinaten der Inputmatrix A.
2. In der nächsten Produktionsperiode wird erwartet, dass die Nachfrage von Produkten der Betriebe $B$ auf $82 M E$ und $R$ auf $84 M E$ sinkt. Betrieb $S$ soll $10 M E$ an den Markt liefern. Berechnen Sie den zugehörigen Produktionsvektor. Nennen Sie die Ursache dafür, dass trotz des Absinkens der Produktion in allen drei Betrieben die Marktabgabe in einem Betrieb steigt. (7 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Gaußverfahren
  Grundgleichung des Leontief-Modells
  $(E - A) * \vec{x} = \vec{y}$
  Gleichung lösen mithilfe des Gauß-Algorithmus
  ,Setze die Einheitsmatrix, Inputmatrix und den neuen Marktvektor in die Grundgleichung des Leontief-Modells.
  $(E - A) * \vec{x} = \vec{y}$
  $E = (\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}), A = (\begin{array}{ccc} 0,4 & 0,2 & 0,3 \\ 0,3 & 0,4 & 0,2 \\ 0,2 & 0,3 & 0,4 \end{array}), \vec{y_{neu}} = (\begin{array}{c} 82 \\ 84 \\ 10 \end{array})$
  $(\begin{array}{ccc} 0,6 & - 0,2 & - 0,3 \\ - 0,1 & 0,6 & - 0,1 \\ 0 & - 0,2 & 0,3 \end{array}) * \vec{x} = (\begin{array}{c} 82 \\ 84 \\ 10 \end{array})$
  Berechne den neuen Produktionsvektor mithilfe des Gauß-Algorithmus.
  $\begin{array}{c} (\begin{array}{rrrc} 0,6 & - 0,2 & - 0,3 & 82 \\ - 0,1 & 0,6 & - 0,1 & 84 \\ 0 & - 0,2 & 0,3 & 10 \end{array}) & \underset{\to}{6 * II + I} & (\begin{array}{rrrc} 0,6 & - 0,2 & - 0,3 & 82 \\ 0 & 3,4 & - 0,9 & 586 \\ 0 & - 0,2 & 0,3 & 10 \end{array}) \\ \underset{\to}{17 * III + II} & (\begin{array}{rrrc} 0,6 & - 0,2 & - 0,3 & 82 \\ \orange 0 & 3,4 & - 0,9 & 586 \\ \orange 0 & \orange 0 & 4,2 & 756 \end{array}) \end{array}$
  Daraus folgt:
  $\begin{array}{l} 4,2 x_{3} = 756 x_{3} = 180 \\ 3,4 x_{2} - 0,9 * 180 = 586 x_{2} = 220 \\ 0,6 x_{1} - 0,2 * 220 - 0,3 * 180 = 82 x_{1} = 300 \end{array}$
  Damit lautet der gesuchte neue Produktionsvektor: $\vec{x_{neu}} = (\begin{array}{c} 300 \\ 220 \\ 180 \end{array})$
  Ursache für steigende Marktabgabe bei S
  Markt: $\vec{y_{alt}} = (\begin{array}{c} 120 \\ 120 \\ 0 \end{array}) \Rightarrow \vec{y_{neu}} = (\begin{array}{c} 82 \\ 84 \\ 10 \end{array})$
  Produktion: $\vec{x_{alt}} = (\begin{array}{c} 400 \\ 300 \\ 200 \end{array}) \Rightarrow \vec{x_{neu}} = (\begin{array}{c} 300 \\ 220 \\ 180 \end{array})$
  Die Produktion ist in allen drei Betrieben tatsächlich gesunken. Eine mögliche Erklärung dafür, dass die Marktabgabe des Betriebs S dennoch gestiegen ist, lautet, dass die Betriebe B und R weniger produzieren und folglich weniger Mengeneinheiten von S benötigen. Dadurch kann Betrieb S mehr Produkte auf den Markt bringen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Verwende die Grundgleichung des Leontief-Modells um den neuen Produktionsvektor zu berechnen.
  Löse die Gleichung mithilfe des Gauß-Algorithmus.
  Vergleiche die alten und neuen Produktion- und Marktvektoren.
3. Die Betriebe entschließen sich mittelfristig auf biologische Betriebsführung umzustellen. Für die Umstellungszeit ergibt sich die neue Inputmatrix
  $A^{*} = (\begin{array}{ccc} 0,4 & 2 - 0,004 t & 0,3 \\ 0,1 & 0,4 & 0,1 \\ 0 & 0,02 (t - 8) & 0,7 \end{array})$
  Dabei ist $t \in [16; 22]$ ein technologieabhängiger Parameter. Berechnen Sie, für welchen Wert von $t$ die Summe der Marktabgaben aller drei Betriebe am größten ist, wenn der Produktionsvektor $\vec{x} = (40 t 10 t 12 t)^{⊤}$ geplant ist.
  Hinweis: Es kann davon ausgegangen werden, dass die Marktabgaben der drei Betriebe für $t \in [16; 22]$ nicht negativ sind. (8 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelpunkt einer Parabel
  Berechnung des neuen Marktvektors $y (t)$
  Setze die Einheitsmatrix, die neue Inputmatrix und den vom Parameter t abhängigen Produktionsvektor $\vec{x}$ in die Grundgleichung des Leontief-Modells.
  $(E - A^{*}) * \vec{x (t)} = \vec{y (t)}$
  $E = (\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}), A^{*} = (\begin{array}{ccc} 0,4 & 2 - 0,004 t & 0,3 \\ 0,1 & 0,4 & 0,1 \\ 0 & 0,02 (t - 8) & 0,7 \end{array}), \vec{x (t)} = (\begin{array}{c} 40 t \\ 10 t \\ 12 t \end{array})$
  $(\begin{array}{ccc} 0,6 & - (2 - 0,004 t) & - 0,3 \\ - 0,1 & 0,6 & - 0,1 \\ 0 & - 0,02 (t - 8) & 0,3 \end{array}) * (\begin{array}{c} 40 t \\ 10 t \\ 12 t \end{array}) = \vec{y (t)}$
  $\vec{y (t)} = (\begin{array}{c} 0,04 t^{2} + 0,4 t \\ 0,8 t \\ - 0,2 t^{2} + 5,2 t \end{array})$ mit $t \in [16; 22]$
  Gemäß dem Hinweis sind die Koordinaten des Marktvektors $\vec{y (t)}$ für $t \in [16; 22]$ nicht negativ, daher muss das hier nicht nachgewiesen oder überprüft werden.
  Damit lautet der neue Marktvektor in Abhängigkeit von t: $\vec{y (t)} = (\begin{array}{c} 0,04 t^{2} + 0,4 t \\ 0,8 t \\ - 0,2 t^{2} + 5,2 t \end{array})$
  Berechnung der maximalen Summe der Marktabgaben
  Die Summe der Marktangaben erhält man durch Addition der drei Koordinaten des neuen Marktvektors $\vec{y (t)}$ . Sei dies $s (t)$ , somit gilt:
  $s (t) = 0,04 t^{2} + 0,4 t + 0,8 t - 0,2 t^{2} + 5,2 t$
  $s (t) = - 0,16 t^{2} + 6,4 t$
  Die Funktion $s$ beschreibt eine nach unten geöffnete Parabel. Das Maximum liegt somit bei dem Scheitel, sofern dieser im Intervall [16;22] liegt.
  Bestimme die erste Ableitung der Funktion s und bestimme das Maximum.
  $s^{'} (t) = - 0,32 + 6,4$
  $s^{'} (t) = 0$
  $t_{0} = 20$
  Da $t_{0} \in [16; 22]$ liegt, wird die Summe aller Marktabgaben für $t_{0} = 20$ maximal.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne den neuen Marktvektor in Abhängigkeit vom Parameter t mit der Grundgleichung des Leontief-Modells.
  Verwende für die Berechnung der Summe der Marktabgaben die drei Koordinaten des neuen Marktvektors y(t).
  Bestimme das Maximum von der Summe der Marktabgaben.

	B	R	S	Markt	Produktion
B	160	60	60	$y_{1}$	400
R	a	120	20	120	300
S	0	60	b	0	200

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$160 + 60 + 60 + y_{1}$	$=$	$400$
	↓	nach $y_{1}$ umformen
$y_{1}$	$=$	$400 - 160 - 60 - 60 = 120$
$a + 120 + 20 + 120$	$=$	$300$
	↓	nach a umformen
$a$	$=$	$300 - 120 - 20 - 120 = 40$
$60 + b$	$=$	$200$
	↓	nach b umformen
$b$	$=$	$200 - 60 = 140$

B II

Berechnung der Parameter a, b und y1

Bedeutung im Sachzusammenhang

Berechnung der Inputmatrix A

Hast du eine Frage oder Feedback?

Grundgleichung des Leontief-Modells

Gleichung lösen mithilfe des Gauß-Algorithmus

Ursache für steigende Marktabgabe bei S

Hast du eine Frage oder Feedback?

Berechnung des neuen Marktvektors y(t)

Berechnung der maximalen Summe der Marktabgaben

Hast du eine Frage oder Feedback?

Berechnung der Parameter a, b und $y_{1}$

Berechnung des neuen Marktvektors $y (t)$