Stochastik, Teil B, Aufgabengruppe 2

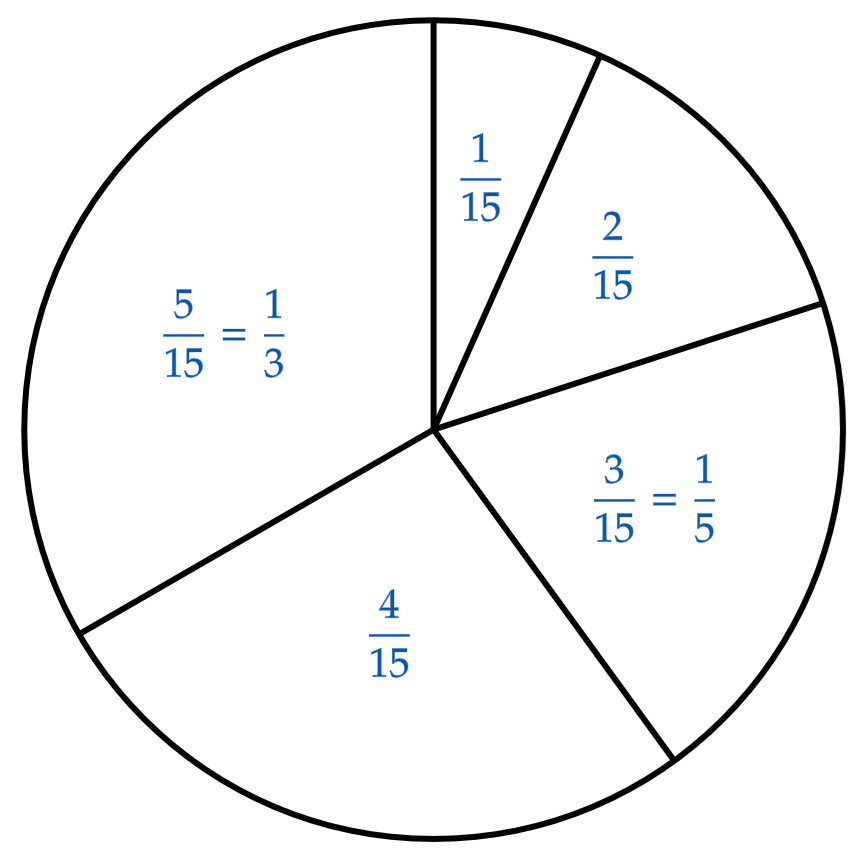
Um Geld für die Ausstattung des örtlichen Kindergartens einzunehmen, veranstaltet der Supermarkt ein Gewinnspiel. Die fünf Sektoren des dabei eingesetzten Glücksrads sind von $1$ bis $5$ durchnummeriert. Die Größe der Sektoren ist direkt proportional zum Zahlenwert der Nummern; beispielsweise ist der Sektor mit der Nummer $3$ dreimal so groß wie der Sektor mit der Nummer $1$ . Nachdem der Spieler sechs Euro bezahlt hat, wird das Glücksrad einmal gedreht. Erzielt der Spieler eine der Nummern $1$ bis $4$ , so wird ihm der zugehörige Zahlenwert als Betrag in Euro ausgezahlt, erzielt er die Nummer $5$ , so erhält er eine Eintrittskarte für einen Freizeitpark im Wert von fünfzehn Euro.

Bestimmen Sie die Größe des Öffnungswinkels des Sektors mit der Nummer $1$ sowie die Wahrscheinlichkeit dafür, dass ein Spieler bei einem Spiel eine Eintrittskarte gewinnt. (Teilergebnis: Größe des Öffnungswinkels: $24^\circ$ ) (3BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Kreisdiagramm
Anteil des Sektors am gesamten Kreis bestimmen
In der Aufgabenstellung ist gegeben, dass
das Glücksrad fünf unterschiedlich große Sektoren hat und
die Sektoren immer x mal so groß sind wie der Sektor 1, der Faktor x ist die Zahl, die in dem Sektor steht,
Man könnte sich den Sektor 2 also von der Größe her als zweimal den Sektor 1 vorstellen, den Sektor 3 als dreimal den Sektor 1 und so weiter.
Insgesamt hätte man dann $1\ +\ 2\ +\ 3\ +\ 4\ +\ 5\ =\ 15$ mal den Sektor 1 im gesamten Glücksrad. Das heißt, der Sektor 1 macht $\frac{1}{15}$ der Kreisfläche des Glücksrades aus.
Öffnungswinkel des Sektors berechnen
Um den Winkel zu bestimmen, multipliziert man jetzt den Anteil des Sektors am Kreis mit der Innenwinkelsumme eines Kreises, also $360^\circ$ :
Wahrscheinlichkeit dafür, dass ein Spieler eine Eintrittskarte gewinnt
Um den zweiten Teil der Aufgabe zu lösen, muss man sich überlegen, wie groß der Sektor 5 ist.
Wir wissen:
Der Sektor 1 macht $\frac{1}{15}$ des gesamten Glücksrades aus.
Sektor 5 ist fünfmal so groß wie Sektor 1.
$\Rightarrow\dfrac{1}{15}\cdot5=\dfrac{5}{15}=\dfrac{1}{3}$
Die Wahrscheinlichkeit dafür, dass ein Spieler bei einem Spiel eine Eintrittskarte gewinnt, beträgt also $\frac{1}{3}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Berechnen Sie den Erwartungswert der Auszahlung pro Spiel, wenn der Gewinn einer Eintrittskarte mit einer Auszahlung von fünfzehn Euro gleichgesetzt wird. Interpretieren Sie das Ergebnis. (4BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Erwartungswert

Erstellen einer Tabelle für die möglichen Ergebnisse der Zufallsgröße X

Den Gesamtgewinn (oder -verlust) des Spielers kann man als Zufallsvariable $X$ bezeichnen. Um herauszufinden, welche Werte $X$ annehmen kann, muss man beachten, dass der Spieler vorher $6 \, \euro$ bezahlen muss, das heißt man muss diesen Betrag noch vom Gewinn abziehen.

Beispiel: Trifft das Glücksrad den dritten Sektor, so bekommt der Spieler $3 \, \euro$ . Der

eigentliche Gewinn beträgt dann

$3 \, \euro \ (=\text{ausbezahlter Gewinn}) \ - \ 6 \, \euro \ (=\text{Spielgebühr}) \ = \ -3 \, \euro$ .

Daraus kann man für alle möglichen Werte von $X$ eine Tabelle erstellen, die auch ihre jeweilige Wahrscheinlichkeit zeigt:

Sektor	1	2	3	4	5
X	$-5$	$-4$	$-3$	$-2$	$9$
P (X=x)	$\dfrac{1}{15}$	$\dfrac{2}{15}$	$\dfrac{3}{15}$	$\dfrac{4}{15}$	$\dfrac{5}{15}$

Berechnen des Erwartungswerts

Mithilfe der Tabelle kann man jetzt den Erwartungswert berechnen:

	$\displaystyle -5 \, \cdot \, \frac{1}{15} \ + \ (-4) \,\cdot \, \frac{2}{15} \ + \ (-3) \,\cdot \, \frac{3}{15} \ + \ (-2) \,\cdot \, \frac{4}{15} \ + \ 9 \,\cdot \, \frac{5}{15}$
$=$	$\displaystyle -\frac{5}{15} \ + \ \biggl(-\frac{8}{15}\biggr) \ + \ \biggl(-\frac{9}{15}\biggr) \ + \ \biggl(-\frac{8}{15}\biggr) \ + \frac{45}{15}$
$=$	$\displaystyle \frac{15}{15}$
$=$	$\displaystyle \underline{\underline{\,1\,}}$

Interpretation des Ergebnisses

Ein Spiel wird als "fair" bezeichnet, wenn der Erwartungswert gleich $0$ ist.

Ist er höher, wird der Spieler im Durchschnitt Gewinn machen, in diesem Fall im Mittel $1 \, \euro$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👇

Der Supermarkt muss für jede Eintrittskarte nur zehn Euro an den Freizeitpark bezahlen. Damit ist bei der Spielaktion ein finanzieller Überschuss zu erwarten, der an den örtlichen Kindergarten gespendet werden soll. Ermitteln Sie den zu erwartenden Überschuss, wenn man davon ausgeht, dass das Spiel insgesamt $6000$ -mal durchgeführt wird. (3BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Erwartungswert

Erwartungswert bestimmen

Wie bei der Teilaufgabe b) kann man auch hier wieder eine Tabelle anlegen, die sich dieses Mal aber auf den Gewinn bzw. Verlust des Supermarkts bezieht. Das heißt, dass ein Gewinn für den Spieler von zum Beispiel $2 \,\euro$ jetzt einen Verlust von $2 \,\euro$ für den Supermarkt bedeuten. Die $6 \,\euro$ Gebühr sind jetzt als $6 \,\euro$ Gewinn zu verstehen und statt $15 \,\euro$ muss man mit $10 \,\euro$ Verlust für eine Eintrittskarte rechnen.

Daraus ergibt sich folgende Tabelle:

Sektor	1	2	3	4	5
X	$5$	$4$	$3$	$2$	$-4$
P(X=x)	$\dfrac{1}{15}$	$\dfrac{2}{15}$	$\dfrac{3}{15}$	$\dfrac{4}{15}$	$\dfrac{5}{15}$

Mithilfe der Tabelle kann man jetzt den Erwartungswert berechnen:

	$\displaystyle 5\cdot\frac{1}{15}+4\cdot\frac{2}{15}+3\cdot\frac{3}{15}+2\cdot\frac{4}{15}-4\cdot\frac{5}{15}$
$=$	$\displaystyle \frac{5}{15}+\frac{8}{15}+\frac{9}{15}+\frac{8}{15}-\frac{20}{15}$
$=$	$\displaystyle \frac{30}{15}-\frac{20}{15}$
$=$	$\displaystyle \frac{10}{15}$
$=$	$\displaystyle \underline{\underline{~\frac{2}{3}~}}$

Der Supermarkt macht bei einem Spiel im Durchschnitt also $\frac{2}{3} \, \euro$ , bzw. $66, \overline {6}$ Cent Gewinn.

Berechnung des Gesamtgewinns

Um den Gesamtgewinn zu berechnen, multipliziert man den durchschnittlichen Gewinn für ein Spiel mit der Anzahl aller Spiele:

\displaystyle \frac{2}{3} \, \euro \, \cdot \, 6000 \ = \ \frac{12000}{3} \, \euro \ = \ 4000 \, \euro

Der Supermarkt kann also einen Überschuss von $4000 \, \euro$ erwarten.

Hast du eine Frage oder Feedback?

Kommentiere hier 👇

Anteil des Sektors am gesamten Kreis bestimmen

Öffnungswinkel des Sektors berechnen

Wahrscheinlichkeit dafür, dass ein Spieler eine Eintrittskarte gewinnt

Hast du eine Frage oder Feedback?

Erstellen einer Tabelle für die möglichen Ergebnisse der Zufallsgröße X

Berechnen des Erwartungswerts

Interpretation des Ergebnisses

Hast du eine Frage oder Feedback?

Erwartungswert bestimmen

Berechnung des Gesamtgewinns

Hast du eine Frage oder Feedback?