Stochastik, Teil B, Aufgabengruppe 2

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

In einem Supermarkt erhalten Kunden abhängig vom Wert ihres Einkaufs eine bestimmte Anzahl von Päckchen mit Tierbildern, die in ein Sammelalbum eingeklebt werden können. Jedes Päckchen enthält fünf Bilder. Im Sammelbuch sind Plätze für insgesamt $200$ verschiedene Bilder vorgesehen. Die Bilder werden jeweils in großer Stückzahl mit der gleichen Häufigkeit produziert und auf die Päckchen zufällig verteilt, wobei sich die Bilder in einem Päckchen nicht unterscheiden müssen.

a) Begründen Sie, dass der Term $\frac{200 \cdot 199 \cdot 198 \cdot 197 \cdot 196}{200^{5}}$ die Wahrscheinlichkeit dafür beschreibt, dass sich in einem Päckchen fünf verschiedene Tierbilder befinden.

b) Einem Jungen fehlen in seinem Sammelalbum noch $15$ Bilder. Er geht mit seiner Mutter zum Einkaufen und erhält anschließend zwei Päckchen mit Tierbildern. Bestimmen Sie die Wahrscheinlichkeit dafür, dass die beiden Päckchen nur Bilder erhalten, die der Junge bereits in seinem Sammelalbum hat.

Bei Kindern besonders beliebt sind die 3D-Bilder, auf denen die Tiere drei-dimensional erscheinen. $20$ der $200$ für ein Sammelalbum vorgesehenen Bilder sind 3D-Bilder.

c) Ermitteln Sie, wie viele Päckchen ein Kind mindestens benötigt, um mit einer Wahrscheinlichkeit von mehr als $99 %$ mindestens ein 3D-Bild zu erhalten.

a)

Um die Wahrscheinlichkeit eines Ereignisses zu berechnen, dividiert man die Anzahl der günstigen durch die Anzahl der möglichen Ereignisse.

Im Zähler steht als Erstes die Zahl $200$ , da es bei der ersten Karte egal ist, welches Tier sie zeigt, da ja noch kein Tier gezogen wurde, mit dem es übereinstimmen könnte.

Bei der zweiten Karte dürfen alle Tiere zu sehen sein, außer das, das auf der ersten Karte ist, das heißt es gibt $200 - 1 = 199$ Möglichkeiten. Auf der dritten Karte dürfen alle Tiere sein außer die auf den ersten beiden Karten, also gibt es $198$ Möglichkeiten, und so weiter.

Im Nenner steht die Anzahl aller Karten, also $200$ , mit $5$ potenziert, da bei der Berechnung aller möglichen Kombinationen jede Karte auch mehrmals vorkommen darf.

b)

Dem Jungen fehlen nur noch $15$ Bilder, das heißt er hat schon $200 - 15 = 185$ . Die Wahrscheinlichkeit, dass er eines zieht, das er schon hat, beträgt also $\frac{185}{200}$ . Da diese Wahrscheinlichkeit bei jedem Bild, das gezogen wird, gleich bleibt, kann man die Endwahrscheinlichkeit wie folgt berechnen:

{(\frac{185}{200})}^{10} \approx 0,4586

Die Wahrscheinlichkeit, dass der Junge die zehn Bildern, die er zieht, alle schon hat, beträgt ca. $45,86 %$ .

c)

Es handelt sich um eine Dreimal-Mindestens-Aufgabe. Wir suchen nach der Wahrscheinlichkeit, mindestens ein 3D-Bild zu erhalten, also muss die Zufallsvariable größer gleich eins gesetzt werden. Die Wahrscheinlichkeit soll höher als $99 %$ sein, also setzen wir ein größer-Zeichen zwischen die beiden Seiten der Ungleichung.

$P (X \geq 1)$	$>$	$0,99$
	↓	Formuliere um in die Gegenwahrscheinlichkeit
$1 - P (X = 0)$	$>$	$0,99$
	↓	20 der 200 Bilder sind 3D-Bilder, das heißt die Wahrscheinlichkeit, ein 3D-Bild zu ziehen, beträgt $\frac{20}{200} = \frac{1}{10} = 0,1$
$1 - ((\binom{n}{0}) \cdot {0,1}^{0} \cdot {0,9}^{n - 0})$	$>$	$0,99$
	↓	Vereinfache
$1 - (1 \cdot 1 \cdot {0,9}^{n})$	$>$	$0,99$
$1 - {0,9}^{n}$	$>$	$0,99$	$- 0,99$
$1 - {0,9}^{n} - 0,99$	$>$	$0$	$+ {0,9}^{n}$
$0,01$	$>$	${0,9}^{n}$	$\ln$
$\ln (0,01)$	$>$	$\ln ({0,9}^{n})$
	↓	Man kann das n vor den $l n ()$ ziehen, da hier die Logarithmusregeln gelten
$\ln (0,01)$	$>$	$n \cdot \ln (0,9)$	$/ \ln (0,9)$
	↓	Hier muss man das Ungleichheitszeichen umdrehen, da durch eine negative Zahl dividiert wird
$\frac{\ln (0,01)}{\ln (0,9)}$	$<$	$n$
	↓	Berechne und runde
$43,71$	$<$	$n$

Ein Kind muss mindestens $44$ Karten ziehen, um mit einer Wahrscheinlichkeit von mindestens $99 %$ mindestens ein 3D-Bild zu erhalten.

2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
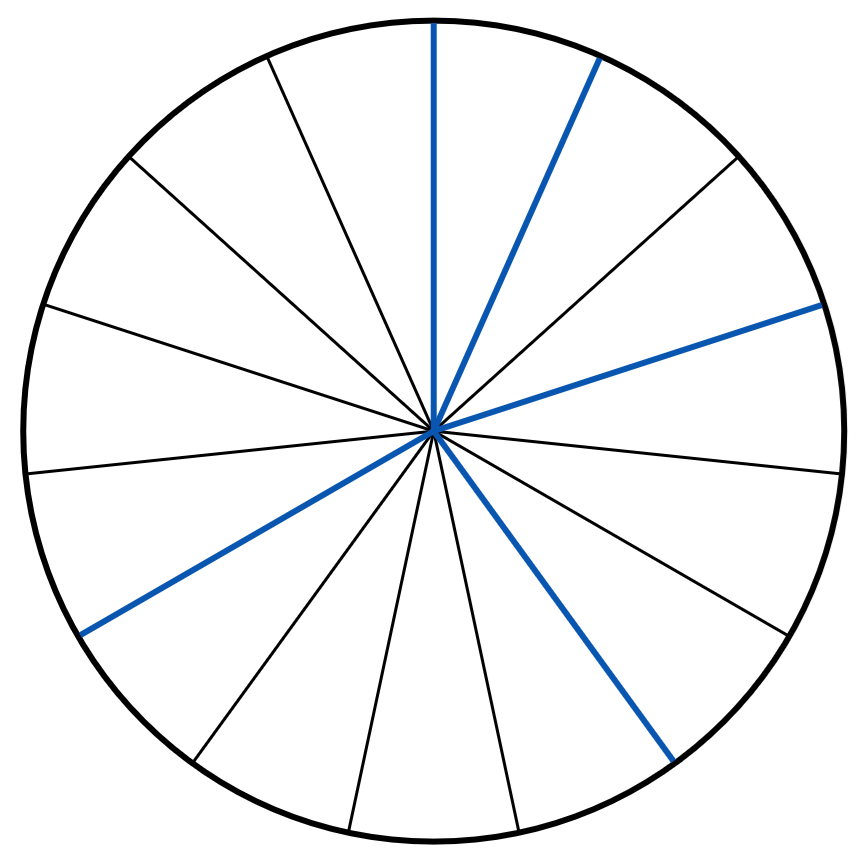
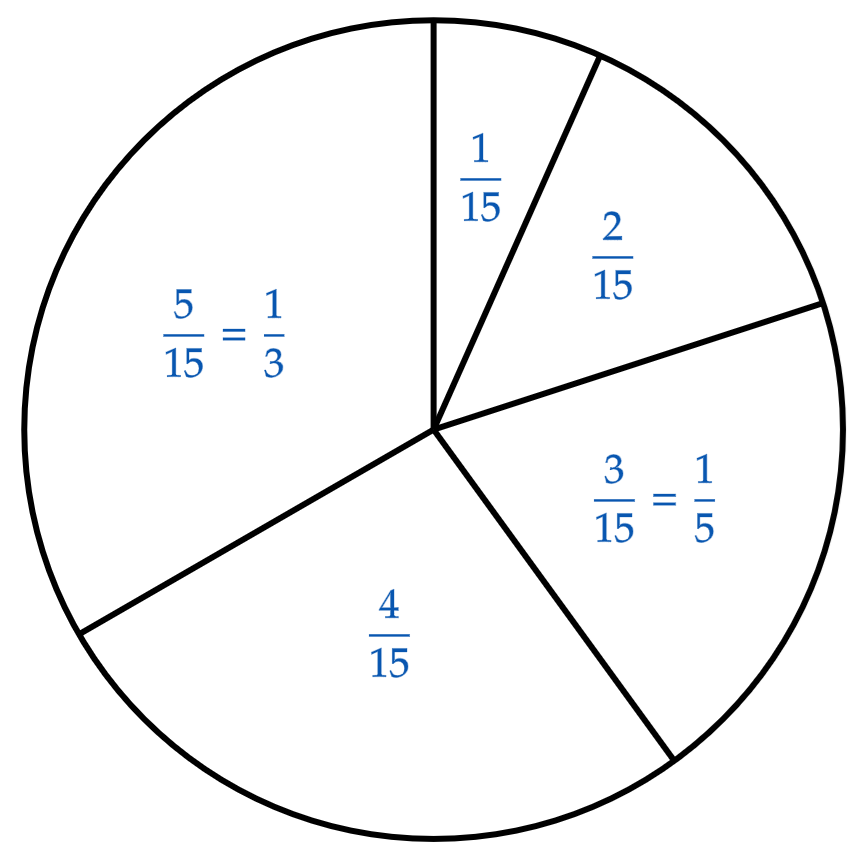
Um Geld für die Ausstattung des örtlichen Kindergartens einzunehmen, veranstaltet der Supermarkt ein Gewinnspiel. Die fünf Sektoren des dabei eingesetzten Glücksrads sind von $1$ bis $5$ durchnummeriert. Die Größe der Sektoren ist direkt proportional zum Zahlenwert der Nummern; beispielsweise ist der Sektor mit der Nummer $3$ dreimal so groß wie der Sektor mit der Nummer $1$ . Nachdem der Spieler sechs Euro bezahlt hat, wird das Glücksrad einmal gedreht. Erzielt der Spieler eine der Nummern $1$ bis $4$ , so wird ihm der zugehörige Zahlenwert als Betrag in Euro ausgezahlt, erzielt er die Nummer $5$ , so erhält er eine Eintrittskarte für einen Freizeitpark im Wert von fünfzehn Euro.
1. Bestimmen Sie die Größe des Öffnungswinkels des Sektors mit der Nummer $1$ sowie die Wahrscheinlichkeit dafür, dass ein Spieler bei einem Spiel eine Eintrittskarte gewinnt. (Teilergebnis: Größe des Öffnungswinkels: $24^{\circ}$ ) (3BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Kreisdiagramm
  Anteil des Sektors am gesamten Kreis bestimmen
  In der Aufgabenstellung ist gegeben, dass
  das Glücksrad fünf unterschiedlich große Sektoren hat und
  die Sektoren immer x mal so groß sind wie der Sektor 1, der Faktor x ist die Zahl, die in dem Sektor steht,
  Man könnte sich den Sektor 2 also von der Größe her als zweimal den Sektor 1 vorstellen, den Sektor 3 als dreimal den Sektor 1 und so weiter.
  Insgesamt hätte man dann $1 + 2 + 3 + 4 + 5 = 15$ mal den Sektor 1 im gesamten Glücksrad. Das heißt, der Sektor 1 macht $\frac{1}{15}$ der Kreisfläche des Glücksrades aus.
  Öffnungswinkel des Sektors berechnen
  Um den Winkel zu bestimmen, multipliziert man jetzt den Anteil des Sektors am Kreis mit der Innenwinkelsumme eines Kreises, also $360^{\circ}$ :
  $360^{\circ} \cdot \frac{1}{15} = 24^{\circ}$
  Wahrscheinlichkeit dafür, dass ein Spieler eine Eintrittskarte gewinnt
  Um den zweiten Teil der Aufgabe zu lösen, muss man sich überlegen, wie groß der Sektor 5 ist.
  Wir wissen:
  Der Sektor 1 macht $\frac{1}{15}$ des gesamten Glücksrades aus.
  Sektor 5 ist fünfmal so groß wie Sektor 1.
  $\Rightarrow \frac{1}{15} \cdot 5 = \frac{5}{15} = \frac{1}{3}$
  Die Wahrscheinlichkeit dafür, dass ein Spieler bei einem Spiel eine Eintrittskarte gewinnt, beträgt also $\frac{1}{3}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Berechnen Sie den Erwartungswert der Auszahlung pro Spiel, wenn der Gewinn einer Eintrittskarte mit einer Auszahlung von fünfzehn Euro gleichgesetzt wird. Interpretieren Sie das Ergebnis. (4BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Erwartungswert
  Erstellen einer Tabelle für die möglichen Ergebnisse der Zufallsgröße X
  Den Gesamtgewinn (oder -verlust) des Spielers kann man als Zufallsvariable $X$ bezeichnen. Um herauszufinden, welche Werte $X$ annehmen kann, muss man beachten, dass der Spieler vorher $6 €$ bezahlen muss, das heißt man muss diesen Betrag noch vom Gewinn abziehen.
  Beispiel: Trifft das Glücksrad den dritten Sektor, so bekommt der Spieler $3 €$ . Der
  eigentliche Gewinn beträgt dann
  $3 € (= ausbezahlter Gewinn) - 6 € (= Spielgebühr) = - 3 €$ .
  Daraus kann man für alle möglichen Werte von $X$ eine Tabelle erstellen, die auch ihre jeweilige Wahrscheinlichkeit zeigt:
  Sektor
  1
  2
  3
  4
  5
  X
  $- 5$
  $- 4$
  $- 3$
  $- 2$
  $9$
  P (X=x)
  $\frac{1}{15}$
  $\frac{2}{15}$
  $\frac{3}{15}$
  $\frac{4}{15}$
  $\frac{5}{15}$
  Berechnen des Erwartungswerts
  Mithilfe der Tabelle kann man jetzt den Erwartungswert berechnen:
  $- 5 \cdot \frac{1}{15} + (- 4) \cdot \frac{2}{15} + (- 3) \cdot \frac{3}{15} + (- 2) \cdot \frac{4}{15} + 9 \cdot \frac{5}{15}$
  $=$ $- \frac{5}{15} + (- \frac{8}{15}) + (- \frac{9}{15}) + (- \frac{8}{15}) + \frac{45}{15}$
  $=$ $\frac{15}{15}$
  $=$ $1$
  Interpretation des Ergebnisses
  Ein Spiel wird als "fair" bezeichnet, wenn der Erwartungswert gleich $0$ ist.
  Ist er höher, wird der Spieler im Durchschnitt Gewinn machen, in diesem Fall im Mittel $1 €$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Betrachte den Gewinn des Spielers als Zufallsgröße X.
  Erstelle eine Tabelle für die Werte, die X annehmen kann. Beachte dabei die Gebühr von $6 €$ , die der Spieler vor dem Spiel bezahlen muss.
  Berechne mithilfe der Tabelle den Erwartungswert. Wenn du nicht mehr weißt, wie das geht, schau hier nach: Erwartungswert
  Erkläre am Schluss, was dein Ergebnis im Sachzusammenhang bedeutet.
3. Der Supermarkt muss für jede Eintrittskarte nur zehn Euro an den Freizeitpark bezahlen. Damit ist bei der Spielaktion ein finanzieller Überschuss zu erwarten, der an den örtlichen Kindergarten gespendet werden soll. Ermitteln Sie den zu erwartenden Überschuss, wenn man davon ausgeht, dass das Spiel insgesamt $6000$ -mal durchgeführt wird. (3BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Erwartungswert
  Erwartungswert bestimmen
  Wie bei der Teilaufgabe b) kann man auch hier wieder eine Tabelle anlegen, die sich dieses Mal aber auf den Gewinn bzw. Verlust des Supermarkts bezieht. Das heißt, dass ein Gewinn für den Spieler von zum Beispiel $2 €$ jetzt einen Verlust von $2 €$ für den Supermarkt bedeuten. Die $6 €$ Gebühr sind jetzt als $6 €$ Gewinn zu verstehen und statt $15 €$ muss man mit $10 €$ Verlust für eine Eintrittskarte rechnen.
  Daraus ergibt sich folgende Tabelle:
  Sektor
  1
  2
  3
  4
  5
  X
  $5$
  $4$
  $3$
  $2$
  $- 4$
  P(X=x)
  $\frac{1}{15}$
  $\frac{2}{15}$
  $\frac{3}{15}$
  $\frac{4}{15}$
  $\frac{5}{15}$
  Mithilfe der Tabelle kann man jetzt den Erwartungswert berechnen:
  $5 \cdot \frac{1}{15} + 4 \cdot \frac{2}{15} + 3 \cdot \frac{3}{15} + 2 \cdot \frac{4}{15} - 4 \cdot \frac{5}{15}$
  $=$ $\frac{5}{15} + \frac{8}{15} + \frac{9}{15} + \frac{8}{15} - \frac{20}{15}$
  $=$ $\frac{30}{15} - \frac{20}{15}$
  $=$ $\frac{10}{15}$
  $=$ $\frac{2}{3}$
  Der Supermarkt macht bei einem Spiel im Durchschnitt also $\frac{2}{3} €$ , bzw. $66, 6$ Cent Gewinn.
  Berechnung des Gesamtgewinns
  Um den Gesamtgewinn zu berechnen, multipliziert man den durchschnittlichen Gewinn für ein Spiel mit der Anzahl aller Spiele:
  $\frac{2}{3} € \cdot 6000 = \frac{12000}{3} € = 4000 €$
  Der Supermarkt kann also einen Überschuss von $4000 €$ erwarten.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne zunächst den durchschnittlichen zu erwartenden Gewinn bei einem Spiel und multipliziere ihn dann mit der Anzahl an Spielen.

Sektor	1	2	3	4	5
X	$- 5$	$- 4$	$- 3$	$- 2$	$9$
P (X=x)	$\frac{1}{15}$	$\frac{2}{15}$	$\frac{3}{15}$	$\frac{4}{15}$	$\frac{5}{15}$

Sektor	1	2	3	4	5
X	$5$	$4$	$3$	$2$	$- 4$
P(X=x)	$\frac{1}{15}$	$\frac{2}{15}$	$\frac{3}{15}$	$\frac{4}{15}$	$\frac{5}{15}$

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

	$- 5 \cdot \frac{1}{15} + (- 4) \cdot \frac{2}{15} + (- 3) \cdot \frac{3}{15} + (- 2) \cdot \frac{4}{15} + 9 \cdot \frac{5}{15}$
$=$	$- \frac{5}{15} + (- \frac{8}{15}) + (- \frac{9}{15}) + (- \frac{8}{15}) + \frac{45}{15}$
$=$	$\frac{15}{15}$
$=$	$1$

	$5 \cdot \frac{1}{15} + 4 \cdot \frac{2}{15} + 3 \cdot \frac{3}{15} + 2 \cdot \frac{4}{15} - 4 \cdot \frac{5}{15}$
$=$	$\frac{5}{15} + \frac{8}{15} + \frac{9}{15} + \frac{8}{15} - \frac{20}{15}$
$=$	$\frac{30}{15} - \frac{20}{15}$
$=$	$\frac{10}{15}$
$=$	$\frac{2}{3}$

Stochastik, Teil B, Aufgabengruppe 2

a)

b)

c)

Anteil des Sektors am gesamten Kreis bestimmen

Öffnungswinkel des Sektors berechnen

Wahrscheinlichkeit dafür, dass ein Spieler eine Eintrittskarte gewinnt

Hast du eine Frage oder Feedback?

Erstellen einer Tabelle für die möglichen Ergebnisse der Zufallsgröße X

Berechnen des Erwartungswerts

Interpretation des Ergebnisses

Hast du eine Frage oder Feedback?

Erwartungswert bestimmen

Berechnung des Gesamtgewinns

Hast du eine Frage oder Feedback?