Analysis, Teil B, Aufgabengruppe 2

Ein Motorboot fährt mit konstanter Motorleistung auf einem Fluss eine Strecke der Länge $10\mathrm{km}$ zuerst flussabwärts und unmittelbar anschließend flussaufwärts zum Ausgangspunkt zurück. Mit der Eigengeschwindigkeit des Motorboots wird der Betrag der Geschwindigkeit bezeichnet, mit der sich das Boot bei dieser Motorleistung auf einem stehenden Gewässer bewegen würde. Im Folgenden soll modellhaft davon ausgegangen werden, dass die Eigengeschwindigkeit des Boots während der Fahrt konstant ist und das Wasser im Fluss mit der konstanten Geschwindigkeit $5\frac{km}h$ fließt. Die für das Wendemanöver erforderliche Zeit wird vernachlässigt. Die Gesamtfahrtzeit in Stunden, die das Boot für Hinfahrt und Rückfahrt insgesamt benötigt, wird im Modell für $x>5$ durch den Term $t(x)=\dfrac{10}{x+5}+\dfrac{10}{x-5}$ angegeben. Dabei ist $x$ die Eigengeschwindigkeit des Boots in $\frac{km}h$ .

Bestimmen Sie auf der Grundlage des Modells für eine Fahrt mit einer Eigengeschwindigkeit von $10\frac{km}h$ und für eine Fahrt mit einer Eigengeschwindigkeit von $20\frac{km}h$ jeweils die Gesamtfahrtzeit in Minuten. (2BE)

Begründen Sie, dass der erste Summand des Terms $t(x)$ die für die Hinfahrt, der zweite Summand die für die Rückfahrt erforderliche Zeit in Stunden angibt.(3BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kürzen von Brüchen
Beim ersten Summanden steht $x+5$ ; beim zweiten $x-5$ im Nenner. Dadurch wird der gesamte erste Summand bei der selben Geschwindigkeit immer kleiner als der zweite. Das entspricht der Hinfahrt (flussabwärts, also schneller) und der Rückfahrt (flussaufwärts, also langsamer).
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Begründen Sie im Sachzusammenhang, das $t(x)$ für $0<x<5$ nicht als Gesamtfahrtzeit interpretiert werden kann. (2BE)

?
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Zeigen Sie, dass die Terme $f(x)=\dfrac{20x}{x^2-25}$ und $t(x)$ äquivalent sind. (2BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kürzen von Brüchen

Wenn man zeigen soll , dass zwei Terme äquivalent sind, kannst du sie gleichsetzen, umformen und prüfen ob die Gleichung für alle $x$ aus der Definitionsmenge stimmt.

Achtung: Du bist fertig, wenn links und rechts vom Gleichheitszeichen das Gleiche steht. Du musst hier nicht nach $x$ auflösen!

$\displaystyle t\left(x\right)$	$=$	$\displaystyle f\left(x\right)$
$\displaystyle \frac{10}{x+5}+\frac{10}{x-5}$	$=$	$\displaystyle \frac{20x}{x^2-25}$
	↓	Bringe die Brüche auf der linken Seite auf den gleichen Hauptnenner.
$\displaystyle \frac{10\cdot\left(x-5\right)}{\left(x+5\right)\left(x-5\right)}+\frac{10\cdot\left(x+5\right)}{\left(x+5\right)\left(x-5\right)}$	$=$	$\displaystyle \frac{20x}{x^2-25}$
	↓	Multipliziere die Klammern aus.
$\displaystyle \frac{\left(10x-50\right)+\left(10x+50\right)}{\left(x+5\right)\left(x-5\right)}$	$=$	$\displaystyle \frac{20x}{x^2-25}$
	↓	Wende im linken Bruch die 3. binomische Formel an und vereinfache weiter den Term.
$\displaystyle \frac{20x}{x^2-25}$	$=$	$\displaystyle \frac{20x}{x^2-25}$

Rechts und links der Gleichung steht nun derselbe Term. Die Funktionsterme sind also äquivalent. Egal, welches $x$ man für $t(x)$ oder $f(x)$ einsetzt, die Funktionswerte sind gleich.

Alternative Lösung

Anstatt die Terme gleichzusetzen, kannst du auch zeigen, dass sie äquivalent sind, indem du einen der Terme stückweise umformst. Am Ende muss der zweite Term herauskommen.

Hier bietet es sich an $t(x)$ umzuformen. $f(x)$ ist ein vereinfachter Bruch. Also probierst du am besten folgendes aus. Bringe den Bruch auf einen Hauptnenner bringst und vereinfachst.

$\displaystyle t\left(x\right)$	$=$	$\displaystyle \frac{10}{x+5}+\frac{10}{x-5}$
	↓	Bringe die Brüche auf der linken Seite auf den gleichen Hauptnenner.
	$=$	$\displaystyle \frac{10\cdot\left(x-5\right)}{\left(x+5\right)\left(x-5\right)}+\frac{10\cdot\left(x+5\right)}{\left(x+5\right)\left(x-5\right)}$
	↓	Multipliziere die Klammern aus.
	$=$	$\displaystyle \frac{\left(10x-50\right)+\left(10x+50\right)}{\left(x+5\right)\left(x-5\right)}$
	↓	Wende die 3. binomische Formel an und vereinfache weiter den Term.
	$=$	$\displaystyle \frac{20x}{x^2-25}$
	$=$	$\displaystyle f\left(x\right)\;\;\; \checkmark$

Hast du eine Frage oder Feedback?

Kommentiere hier 👇

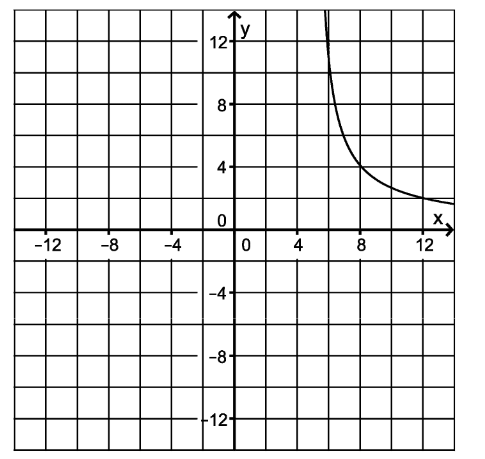
Beschreiben Sie, wie man mithilfe der Abbildung für eine Fahrt mit einer Gesamtfahrtzeit zwischen zwei und vierzehn Stunden die zugehörige Eigengeschwindigkeit des Boots näherungsweise ermitteln kann. Berechnen Sie auf der Grundlage des Modells die Eigengeschwindigkeit des Boots für eine Fahrt mit einer Gesamtfahrtzeit von vier Stunden.(5BE)

?
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

$\displaystyle t\left(10\right)$	$=$	$\displaystyle \frac{10}{10+5}+\frac{10}{10-5}$
	$=$	$\displaystyle \frac{10}{15}+\frac{10}{5}$
	↓	Bring die Brüche auf den selben Hauptnenner durch Erweitern.
	$=$	$\displaystyle \frac{10\cdot5}{15\cdot5}+\frac{10\cdot15}{5\cdot15}$
	$=$	$\displaystyle \frac{50}{75}+\frac{150}{75}$
	$=$	$\displaystyle \frac{200}{75}$
	↓	Kürzen.
	$=$	$\displaystyle \frac{8}{3}$
	$=$	$\displaystyle 2,\overline{6}$

$\displaystyle t\left(20\right)$	$=$	$\displaystyle \frac{10}{20+5}+\frac{10}{20-5}$
	$=$	$\displaystyle \frac{10}{25}+\frac{10}{15}$
	↓	Bring die Brüche auf den selben Hauptnenner durch Erweitern.
	$=$	$\displaystyle \frac{10\cdot15}{25\cdot15}+\frac{10\cdot25}{15\cdot25}$
	$=$	$\displaystyle \frac{150}{375}+\frac{250}{375}$
	$=$	$\displaystyle \frac{400}{375}$
	$=$	$\displaystyle \frac{16}{15}$
	$=$	$\displaystyle 1{,}0\overline{6}$