Analysis, Teil B, Aufgabengruppe 2
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
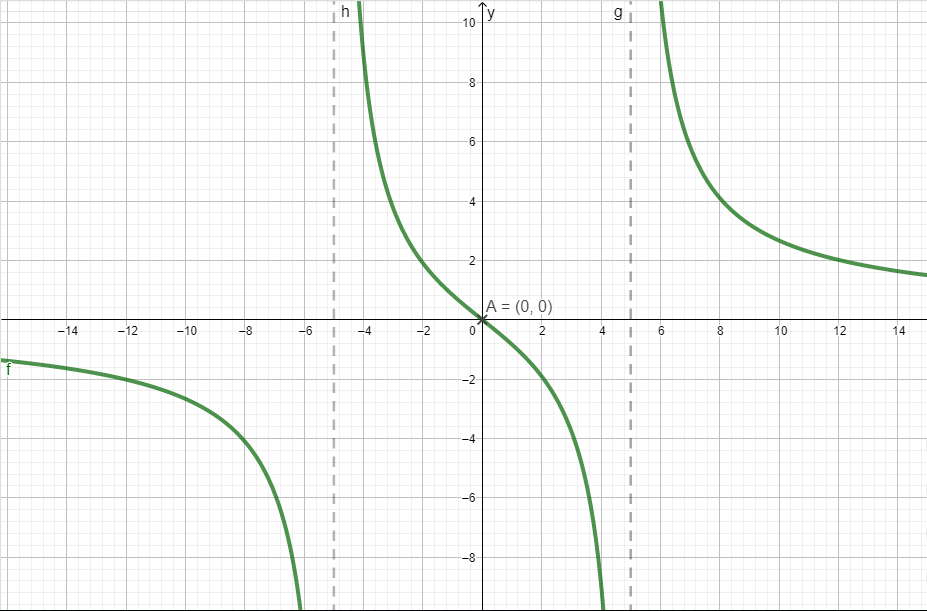
Gegeben ist die Funktion mit und maximalem Definitionsbereich . Die Abbildung zeigt einen Teil des Graphen von .
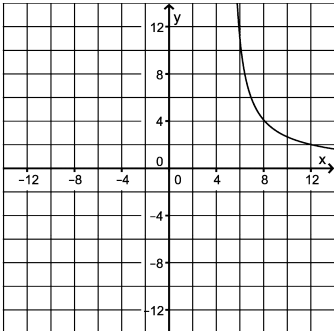
Zeigen Sie, dass gilt und dass symmetrisch bezüglich des Koordinatenursprungs ist. Geben Sie die Nullstelle von sowie die Gleichungen der drei Asymptoten von an.(5BE)
Weisen Sie nach, dass die Steigung von in jedem Punkt des Graphen negativ ist. Berechnen Sie die Größe des Winkels, unter dem die -Achse schneidet.(4BE)
Skizzieren Sie in der Abbildung den darin fehlenden Teil von unter Berücksichtigung der bisherigen Ergebnisse.(3BE)
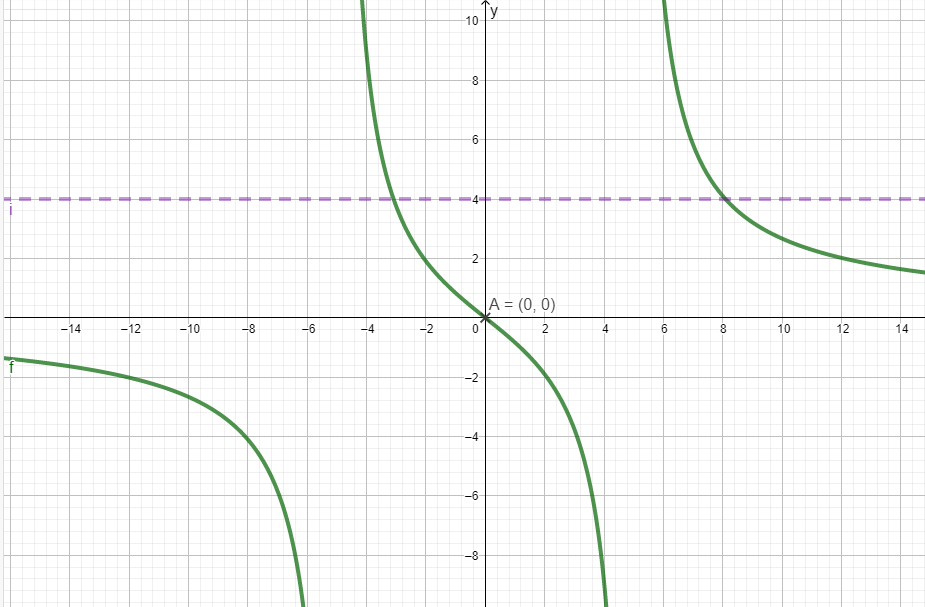
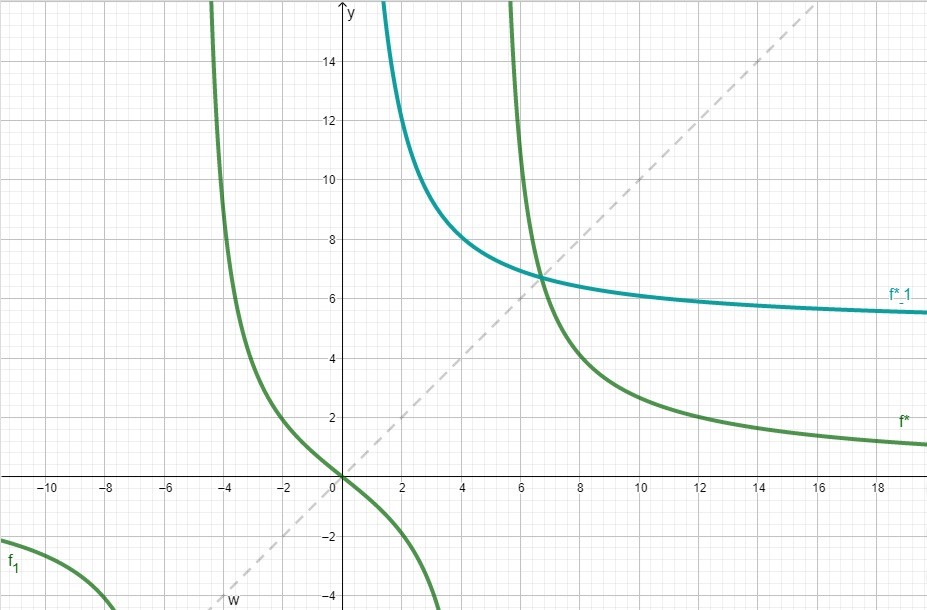
Die Funktion mit Definitionsbereich unterscheidet sich von der Funktion nur hinsichtlich des Definitionsbereichs. Begründen Sie, dass die Funktion nicht umkehrbar ist, die Funktion dagegen schon. Zeichnen Sie den Graphen der Umkehrfunktion von in die Abbildung ein.(4BE)
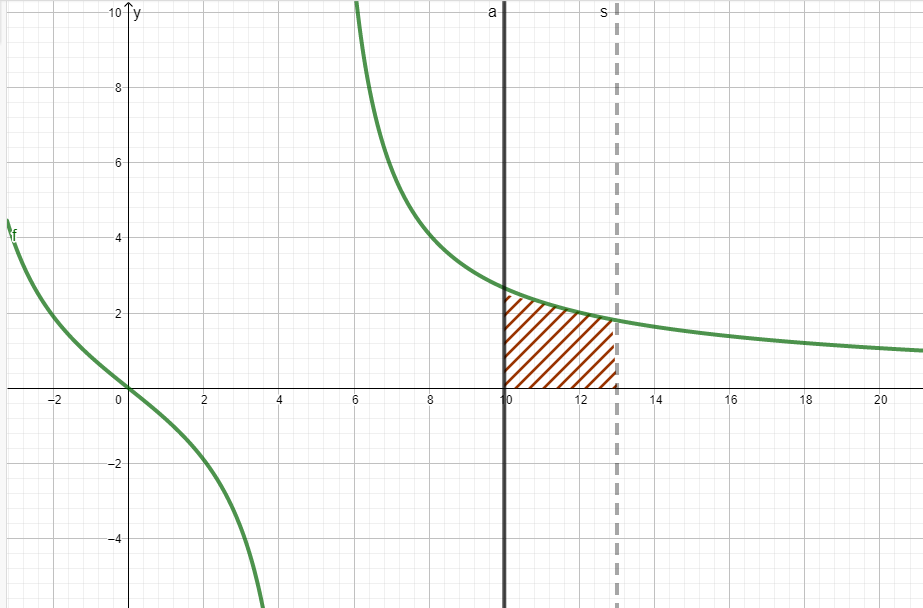
Der Graph von , die -Achse sowie die Geraden mit den Gleichungen und mit schließen ein Flächenstück mit dem Inhalt ein. Bestimmen Sie . (Ergebnis: )(5BE)
Ermitteln Sie so, dass das Flächenstück aus Aufgabe 1e den Inhalt 100 besitzt.(3BE)
Bestimmen Sie das Verhalten von für .(2BE)
- 2
Ein Motorboot fährt mit konstanter Motorleistung auf einem Fluss eine Strecke der Länge zuerst flussabwärts und unmittelbar anschließend flussaufwärts zum Ausgangspunkt zurück. Mit der Eigengeschwindigkeit des Motorboots wird der Betrag der Geschwindigkeit bezeichnet, mit der sich das Boot bei dieser Motorleistung auf einem stehenden Gewässer bewegen würde. Im Folgenden soll modellhaft davon ausgegangen werden, dass die Eigengeschwindigkeit des Boots während der Fahrt konstant ist und das Wasser im Fluss mit der konstanten Geschwindigkeit fließt. Die für das Wendemanöver erforderliche Zeit wird vernachlässigt. Die Gesamtfahrtzeit in Stunden, die das Boot für Hinfahrt und Rückfahrt insgesamt benötigt, wird im Modell für durch den Term angegeben. Dabei ist die Eigengeschwindigkeit des Boots in .
Bestimmen Sie auf der Grundlage des Modells für eine Fahrt mit einer Eigengeschwindigkeit von und für eine Fahrt mit einer Eigengeschwindigkeit von jeweils die Gesamtfahrtzeit in Minuten. (2BE)
Begründen Sie, dass der erste Summand des Terms die für die Hinfahrt, der zweite Summand die für die Rückfahrt erforderliche Zeit in Stunden angibt.(3BE)
Begründen Sie im Sachzusammenhang, das für nicht als Gesamtfahrtzeit interpretiert werden kann. (2BE)
Zeigen Sie, dass die Terme und äquivalent sind. (2BE)
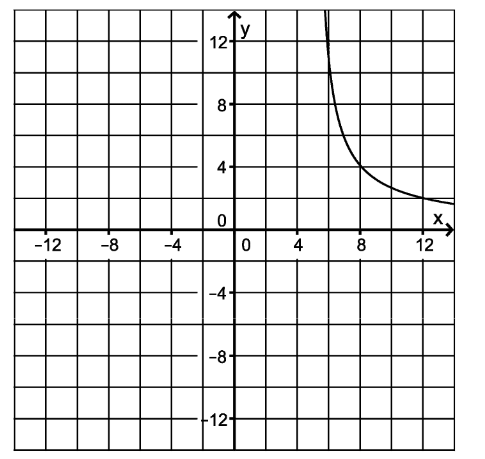
Beschreiben Sie, wie man mithilfe der Abbildung für eine Fahrt mit einer Gesamtfahrtzeit zwischen zwei und vierzehn Stunden die zugehörige Eigengeschwindigkeit des Boots näherungsweise ermitteln kann. Berechnen Sie auf der Grundlage des Modells die Eigengeschwindigkeit des Boots für eine Fahrt mit einer Gesamtfahrtzeit von vier Stunden.(5BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?