Transformationen

Was versteht man unter Transformationen?

Das Wort "Transformation" hat seinen Ursprung im Lateinischen und bedeutet so viel wie "Umwandlung." Es wird also sozusagen eine Funktion in eine andere Funktion umgewandelt, wodurch sich auch ein entsprechender Graph ergibt, der sich um einige wesentliche Punkte von dem Graphen unterscheidet, aus dem er quasi "entstanden" ist. Somit kann man eine Funktion algebraisch oder/und geometrisch transformieren, es kommt allerdings über beide Wege derselbe Funktionsterm, bzw. Graph bei der Transformation heraus.

Die einzelnen Parameter

Eine typische Aufgabenstellung könnte lauten: Gegeben sei die Funktion $f(x)=x^4$. Der Graph der Funktion $g(x)$ soll nun um drei Einheiten nach rechts in x-Richtung und um zwei Einheiten nach unten in y-Richtung verschoben werden. Geben Sie den Funktionsterm von $g(x)$ an.

Verschiebung in y-Richtung

Bevor wir uns mit dieser Aufgabe beschäftigen, sehen wir zunächst einmal, wie man Graphen überhaupt verschiebt, betrachten wir also zunächst einmal den geometrischen Aspekt. Dieses Applet zeigt die Auswirkungen der einzelnen Parameter auf die Transformation des Graphen. Wir sehen also, dass der Parameter b den Graphen in y-Richtung verschiebt. Allerdings heißt b nicht immer b; so kann es vorkommen, dass im Mathebuch von b und auf einer Seite online vom Parameter c gesprochen wird. Daher ist es sinnvoll, sich den Platz dieses Parameters im Funktionsterm anzusehen.

Beispiel:

$f(x) =x^4$

$g(x)=x^4+\textcolor{009999}{3}$

Dabei ist mit diesem Parameter allerdings nicht einfach der y-Achsenabschnitt gemeint. Der gesamte Graph wird um b-Einheiten in y-Richtung verschoben.

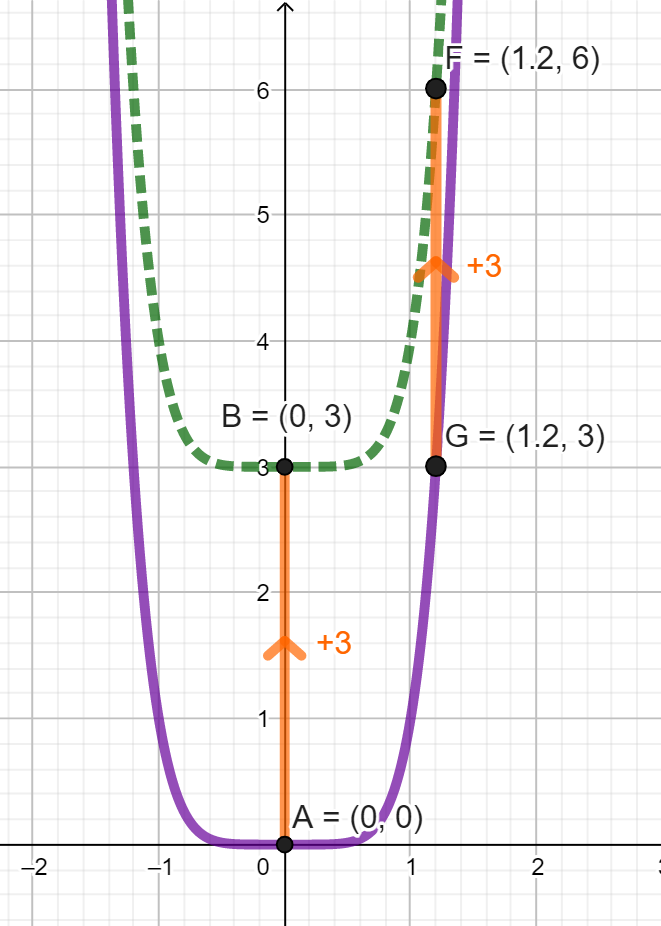
Auf diesem Bild kann man erkennen, dass jeder einzelne Punkt auf dem Graphen um drei Einheiten nach oben verschoben wurde.

Verschiebung in x-Richtung

Neben dem oben beschriebenen Parameter gibt es auch einen Parameter, der den Graphen in x-Richtung verschiebt, in diesem Artikel mit d bezeichnet.