Das Experiment ist ein zweistufiges Zufallsexperiment

$1.$ Stufe: Werfen eines Laplace-Würfels und Beachten ob Augenzahl $6$ oder $\overline{6}$

$\Omega_1=\{6;\overline{6}\}$= mit $P({6})=\frac{1}{6};P({\overline{6}})=\frac{5}{6}$

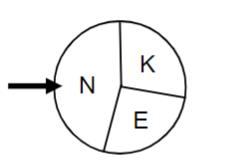
$2.$ Stufe: Drehen einer Drehscheibe und Beachten der Sektoren $N,K$ odee $E$

$\Omega_2=\{N,K,E\}$ mit $P(N)=\frac{160}{360}=\frac{4}{9}$;

Es gilt: $P(K\cup E)=1-\frac{4}{9}=\frac{5}{9}$

Da die Ereignisse $K$ und $E$ unvereinbar sind, gilt $P(K\cap E)=0$.

Somit folgt aus $P(K\cup E)=P(K)+P(E)-P(K\cap E)$, dass $P(K\cup E)=P(K)+P(E)$ ist.

Wählt man $P(K)=p$ und $P(E)=q$, so ist $p+q=1-\frac{4}{9}=\frac{5}{9}$.

Bestimmung der Mittelpunktswinkel

Zur Bestimmung der Mittelpunktswinkel muss man die Wahrscheinlichkeiten $p$ und $q$ ermitteln.

Das Zufallsexperiment 'Drehen einer Drehscheibe' wird nur durchgeführt, wenn das Ergebnis des Zufallsexperimentes 'Werfen eines Laplace-Würfels' Augenzahl $6$

Im bedingten Wahrscheinlichkeitsraum gilt:

$p(B|A)=\frac{P(A\cap B)}{P(A)}\\\Rightarrow P(A\cap B)=P(A)\cdot P(B|A)$

Falls die Ereignisse $A$ und $B$ unabhängig sind, gilt $A(A\cap B)=P(A)\cdot P(B)$

Da die Ereignisse beim 'Werfen eines Laplace-Würfels' und die Ereignisse beim 'Drehen der Drehscheibe' unabhängig sind, gilt hier:

$P(\{6\}|N)=P(\{6\})\cdot P(N)$

Damit hat man:

Für den Gewinn $G=0\Rightarrow P(G=0)=\frac{1}{6}\cdot \frac{4}{9}+\frac{5}{6}$

Für den Gewinn $G=28\Rightarrow P(G=28)=\frac{1}{6}\cdot p$

Für den Gewinn $G=36\Rightarrow P(G=36)=\frac{1}{6}\cdot (\frac{5}{9}-p)$

Für den Erwartungswert gilt $E(X)=3.$

$E(X)=G_1\cdot P(X=G_1)+G_2\cdot P(X=G_2)+G_3\cdot P(X=G_3)=3\\ \iff 0\cdot (\frac{1}{6}\cdot \frac{4}{9}+\frac{5}{6})+\frac{1}{6}\cdot\{28\cdot p+36\cdot (\frac{5}{9}-p)\}=3\\ \iff 18=28\cdot p+36\cdot \frac{5}{9}-36\cdot p\\ \iff 18=28\cdot p+\frac{4\cdot 9\cdot 5}{9}-36\cdot p\\ \iff 18=28\cdot p+20-36\cdot p\\ \iff -2=-8\cdot p\\ \iff p=\frac{1}{4}$

Damit ist $q=\frac{5}{9}-\frac{1}{4}\\ \iff q=\frac{20-9}{36}\\ \iff q=\frac{11}{36}\\ \iff q=\frac{110}{360}$

Damit ist der Mittelpunktswinkel beim Ereignis $N$ gerade $160^\circ$, beim Ereignis $K$ genau $90^\circ$ und beim Ereignis $E$ ist der Mittelpunktswinkel $110^\circ$.