Stochastik, Teil B, Aufgabengruppe 1
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
An einem Samstagvormittag kommen nacheinander vier Familien zum Eingangsbereich eines Freizeitparks. Jede der vier Familien bezahlt an einer der sechs Kassen, wobei davon ausgegangen werden soll, dass jede Kasse mit der gleichen Wahrscheinlichkeit gewählt wird. Beschreiben Sie im Sachzusammenhang zwei Ereignisse A und B, deren Wahrscheinlichkeiten sich mit den folgenden Termen berechnen lassen. (3P)
;
- 2
Im Eingangsbereich des Freizeitparks können Bollerwagen ausgeliehen werden. Erfahrungsgemäß nutzen % der Familien dieses Angebot. Die Zufallsgröße beschreibt die Anzahl der Bollerwagen, die von den ersten Familien, die an einem Tag den Freizeitpark betreten, entliehen werden. Im Folgenden wird davon ausgegangen, dass eine Familie höchstens einen Bollerwagen ausleiht und dass die Zufallsgröße binomialverteilt ist
Bestimmen Sie die Wahrscheinlichkeit dafür, dass mindestens Bollerwagen ausgeliehen werden. (2P)
%Bestimmen Sie die Wahrscheinlichkeit dafür, dass die fünfte Familie die erste ist, die einen Bollerwagen ausleiht. (2P)
%Ermitteln Sie unter Zuhilfenahme des Tafelwerks den kleinsten symmetrisch um den Erwartungswert liegenden Bereich, in dem die Werte der Zufallsgröße mit einer Wahrscheinlichkeit von mindestens % liegen. (5P)
- 3
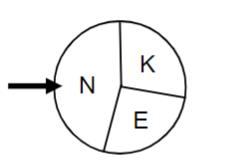
Der Freizeitpark veranstaltet ein Glücksspiel, bei dem Eintrittskarten für den Freizeitpark gewonnen werden können. Zu Beginn des Spiels wirft man einen Würfel, dessen Seiten mit den Zahlen 1 bis 6 durchnummeriert sind. Erzielt man dabei die Zahl 6, darf man anschließend einmal an einem Glücksrad mit drei Sektoren drehen (siehe schematische Abbildung unten). Wird Sektor erzielt, gewinnt man eine Kinderkarte im Wert von Euro, bei Sektor eine Erwachsenenkarte im Wert von Euro. Bei Sektor geht man leer aus. Der Mittelpunktswinkel des Sektors N beträgt 160°. Die Größen der Sektoren und sind so gewählt, dass pro Spiel der Gewinn im Mittel drei Euro beträgt. Bestimmen Sie die Größe der Mittelpunktswinkel der Sektoren und . (6P)
- 4
Am Ausgang des Freizeitparks gibt es einen Automaten, der auf Knopfdruck einen Anstecker mit einem lustigen Motiv bedruckt und anschließend ausgibt. Für den Druck wird aus verschiedenen Motiven eines zufällig ausgewählt, wobei jedes Motiv die gleiche Wahrscheinlichkeit hat. Ein Kind holt sich drei Anstecker aus dem Automaten.
Bestimmen Sie für den Fall die Wahrscheinlichkeit dafür, dass nicht alle drei Anstecker dasselbe Motiv haben. (2P)
Begründen Sie, dass die Wahrscheinlichkeit dafür, dass sich drei verschiedene Motive auf den Ansteckern befinden, den Wert
hat. (2P)
Bestimmen Sie, wie groß mindestens sein muss, damit die Wahrscheinlichkeit dafür, dass sich drei verschiedene Motive auf den Ansteckern befinden, größer als % ist. (3P)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
