Komplexe Zahlen in Polarform

Eine komplexe Zahl $z=x+i\cdot y$ kannst du in Polarform umschreiben zu:

\displaystyle z=r\left(\cos\left(\alpha\right)+i\cdot\sin\left(\alpha\right)\right)

Anschaulich ist $r$ in der Gaußschen Zahlenebene der Abstand der komplexen Zahl vom Ursprung und $\alpha$ der Winkel, den die Linie mit der $x$ -Achse einschließt.

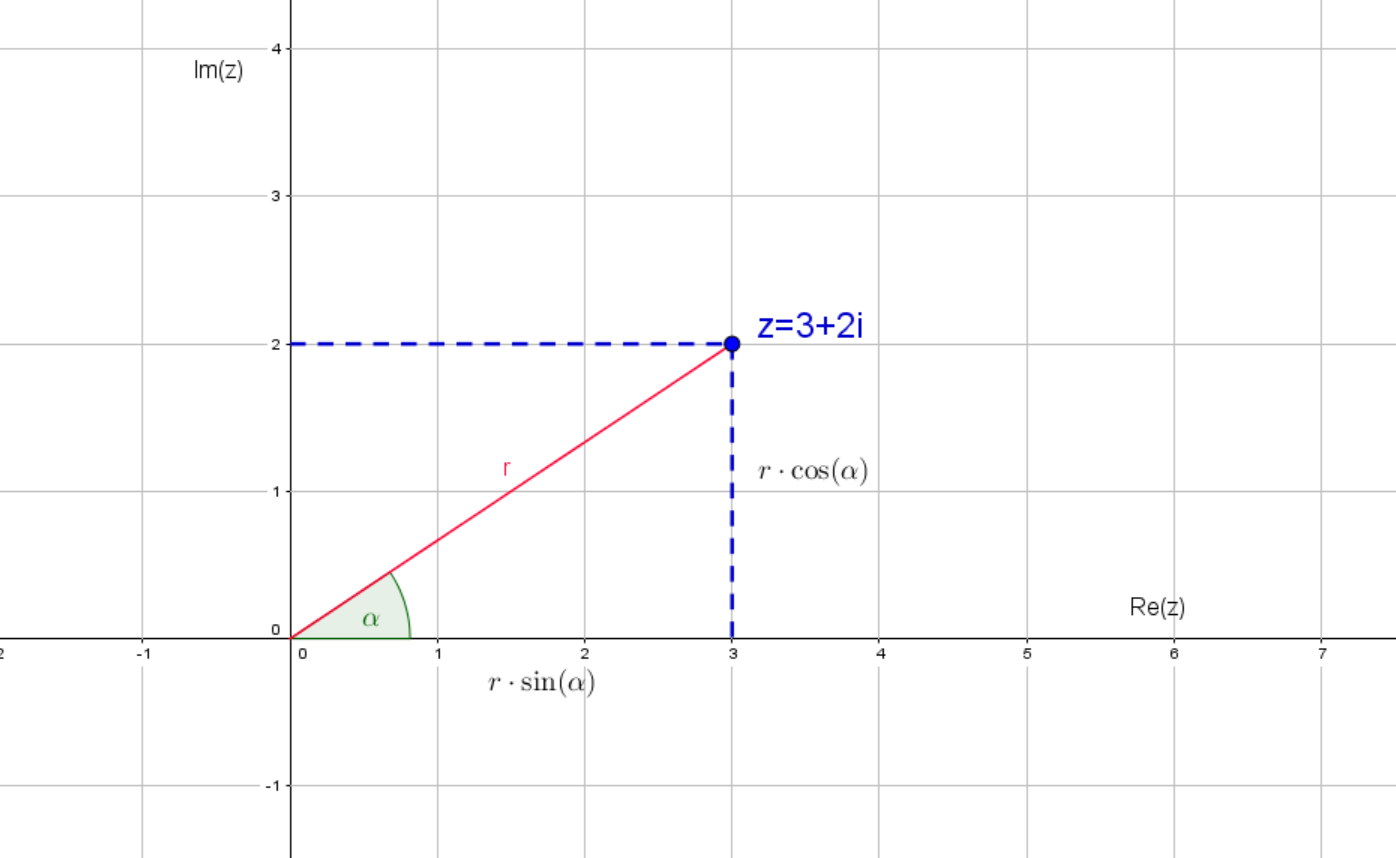
Analog zu den Polarkoordinaten können auch komplexe Zahlen in Polarform dargestellt werden.

In der Gaußschen Zahlenebene haben wir eine komplexe Zahl $z=x+i\cdot y$ durch ihren Realteil $x$ und ihren Imaginärteil $y$ in ein Koordinatensystem eingetragen.

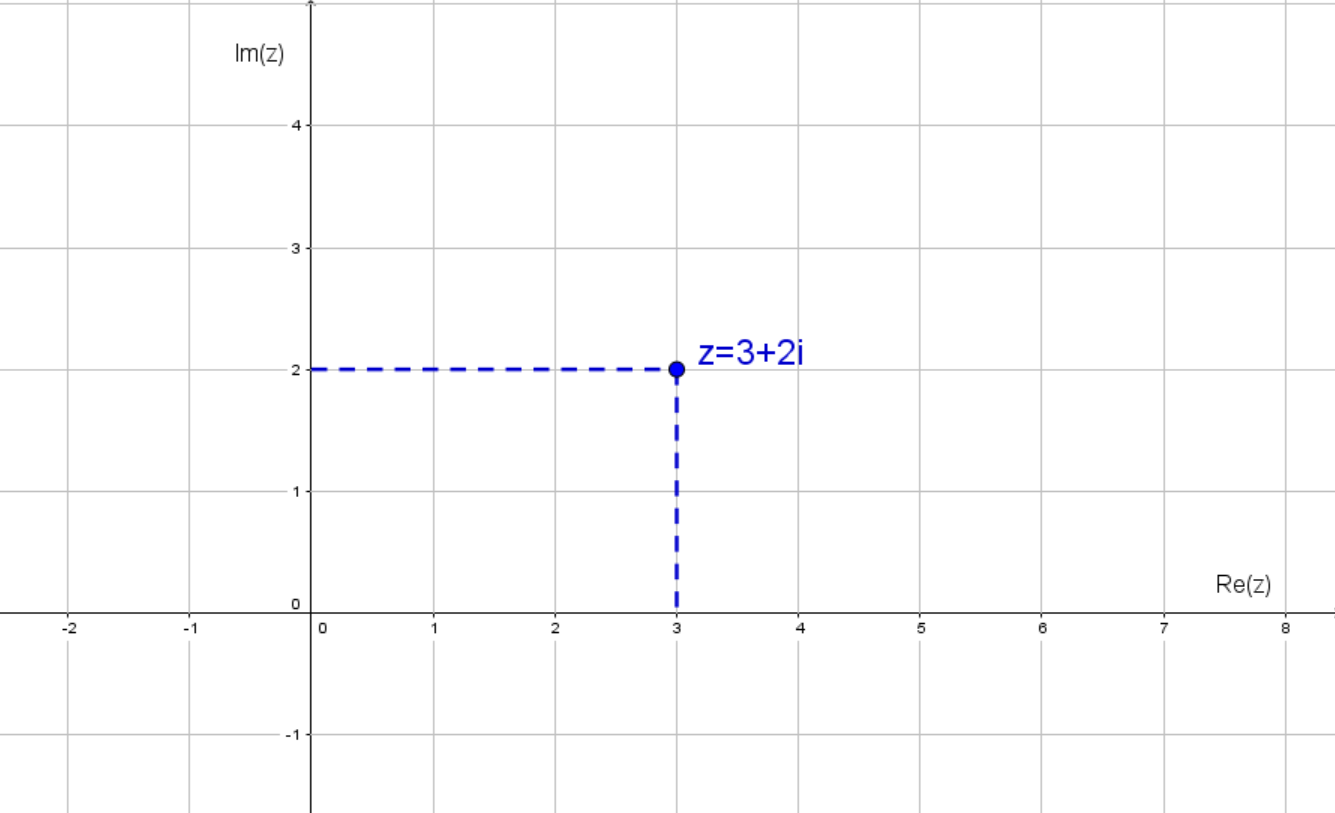
Für ist der Realteil und der Imaginärteil . Wir tragen daher in unserem Koordinatensystem den Punkt ein. — Für $z = 3 + 2 i$ ist der Realteil $3$ und der Imaginärteil $2$ . Wir tragen daher in unserem Koordinatensystem den Punkt $\left(3{,}2\right)$ ein.

Statt $x$ und $y$ können wir eine komplexe Zahl aber auch durch ihren Abstand vom Ursprung und dem Winkel zur $x$ -Achse charakterisieren.

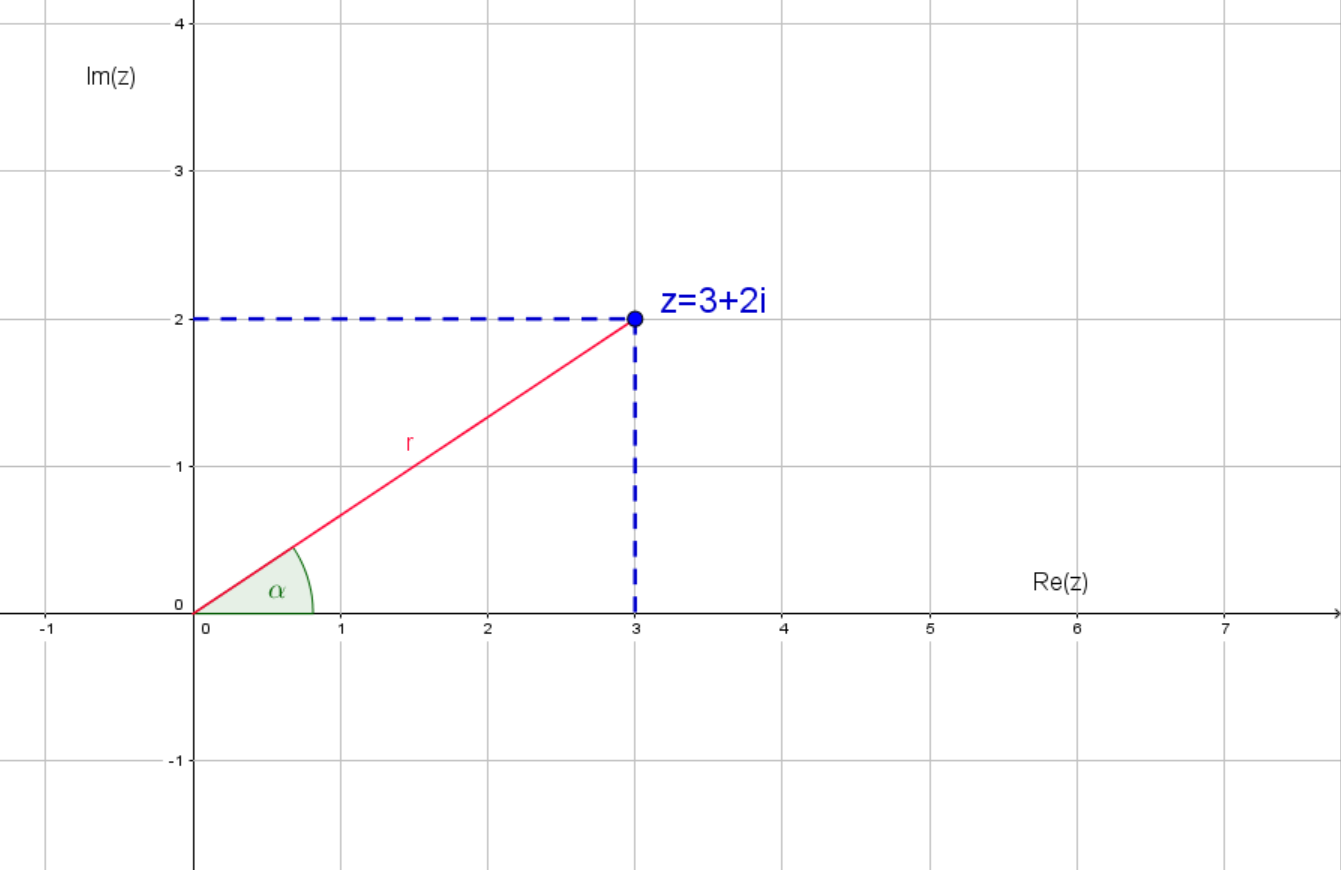
Durch die - und -Koordinate ist ein Punkt eindeutig definiert. Aber auch, indem wir den Abstand zum Ursprung und den eingeschlossenen Winkel mit der -Achse angeben, erhalten wir einen eindeutigen Punkt. — Durch die $x$ - und $y$ -Koordinate ist ein Punkt eindeutig definiert. Aber auch, indem wir den Abstand $r$ zum Ursprung und den eingeschlossenen Winkel $\alpha$ mit der $x$ -Achse angeben, erhalten wir einen eindeutigen Punkt.

Der Abstand der komplexen Zahl vom Ursprung ist der Betrag $r$ . Den Winkel $\alpha$ , den diese Linie mit der $x$ -Achse einschließt, nennen wir das Argument der komplexen Zahl. Es wird normalerweise im Bogenmaß angegeben. $\alpha$ nimmt daher Werte zwischen $0$ und $2 \pi$ an.

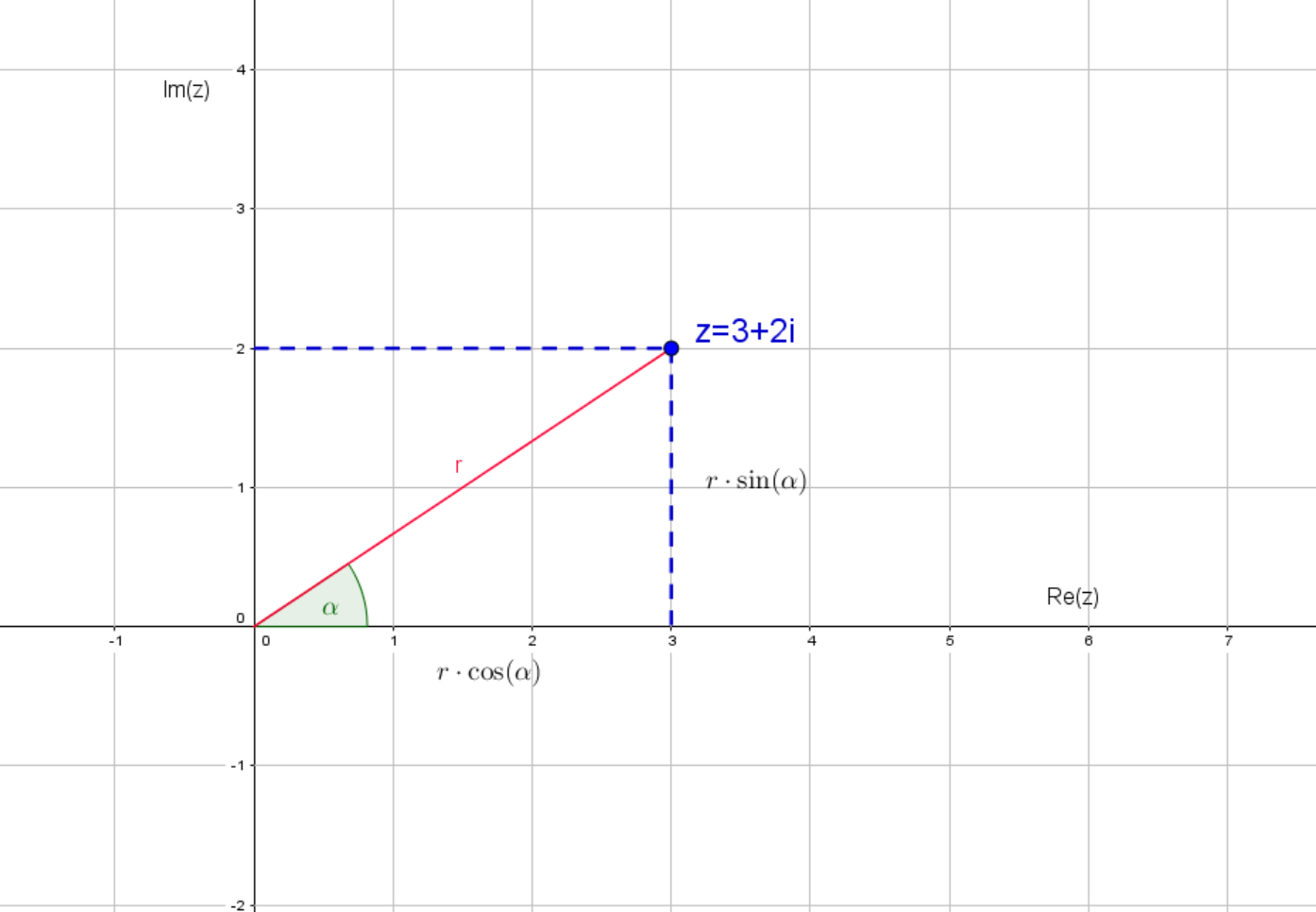
Aus der Abbildung können wir jetzt mit Sinus und Cosinus $x$ und $y$ berechnen:

$\cos\left(\alpha\right)=\frac{x}{r}\Rightarrow x=r\cdot\cos(\alpha)$

$\sin(\alpha)=\frac{y}{r}\Rightarrow y=r\cdot\sin(\alpha)$

Diese Gleichungen für $x$ und $y$ setzen wir jetzt in die kartesische, also die normale Darstellung der komplexen Zahl $z = x + i y$ ein:

$z=x+i\cdot y=r\cdot\cos\left(\alpha\right)+i\cdot r\cdot\sin\left(\alpha\right)=r\left(\cos\left(\alpha\right)+i\cdot\sin\left(\alpha\right)\right)$

Wir können eine komplexe Zahl auch schreiben als:

\displaystyle z=r(\cos(\alpha)+i\cdot\sin(\alpha))

Oft notiert man abkürzend:

\displaystyle z=\left(r | \alpha \right)

Das ist die Darstellung einer komplexen Zahl in den Polarkoordinaten.

Transformationen zu anderen Darstellungsformen

Umrechnung von Polarform in kartesische Form

Wenn $r$ und $\alpha$ bekannt sind, kannst du $x$ und $y$ so berechnen:

$x=r\cdot\cos\left(\alpha\right)$

$y=r\cdot\sin\left(\alpha\right)$

Dann kannst du $x$ und $y$ in $z = x + i y$ einsetzen, um die kartesische Form zu erhalten.

Umrechnung von kartesischer Form in Polarform

Du hast die Darstellung $z = x + i y$ gegeben. $x$ und $y$ kannst du daraus ablesen. Wir wollen nun den Betrag $r$ und das Argument $\alpha$ berechnen.

Für $r$ kannst du die Formel für den Betrag einer komplexen Zahl verwenden:

$r=\sqrt{x^2+y^2}$

Aus der Abbildung oben kannst du ablesen, dass $\tan(\alpha)=\frac{y}{x}$ gilt. Also ist:

$\alpha=\tan^{-1}(\frac{y}{x})$

Weil der Tangens periodisch ist, liefert er zwei mögliche Werte für $\alpha$ :

Einmal den Wert, den du mit der obigen Formel berechnen kannst
und zum anderen den Wert $\alpha'=\pi+\tan^{-1}(\frac{y}{x})$

Um herauszufinden, welcher $\alpha$ -Wert der gesuchte ist, kannst du beide Werte in die Formeln $x=r \cos(\alpha)$ und $y=r \sin(\alpha)$ einsetzen und überprüfen, wo das Richtige herauskommt. Eine Probe ist also in diesem Fall unabdinglich!

Multiplikation und Division komplexer Zahlen in Polarform

MerkeMultiplikation

Bei der Multiplikation zweier komplexer Zahlen $z_{1}$ und $z_{2}$ werden die Radien multipliziert und die Winkel addiert:

\displaystyle z_1\cdot z_2=(r_1\cdot r_2|\alpha_1+\alpha_2)=r_1r_2(\cos(\alpha_1+\alpha_2)+i\cdot\sin(\alpha_1+\alpha_2))

MerkeDivision

Bei der Division zweier komplexer Zahlen $z_{1}$ und $z_{2}$ werden die Radien dividiert und die Winkel subtrahiert:

$\frac{z_1}{z_2}=(\frac{r_1}{r_2}|\alpha_1-\alpha_2)=\frac{r_1}{r_2}(\cos(\alpha_1-\alpha_2)+i\cdot\sin(\alpha_1-\alpha_2))$

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?