Polarkoordinaten

Neben den üblichen kartesischen Koordinaten (" $x$ -/ $y$ -Koordinate") kann man jeden Punkt einer Ebene auch mit Polarkoordinaten beschreiben.

Denn jeder Punkt $P$ ist durch die Angabe folgender zwei Werte eindeutig festgelegt:

Entfernung $r$ des Punktes vom Koordinatenursprung
Winkel $\varphi$ zwischen der positiven x-Achse und der Strecke $[O P]$

Das Paar $(r|\varphi)$ nennt man Polarkoordinaten.

BeispielPolarkoordinaten

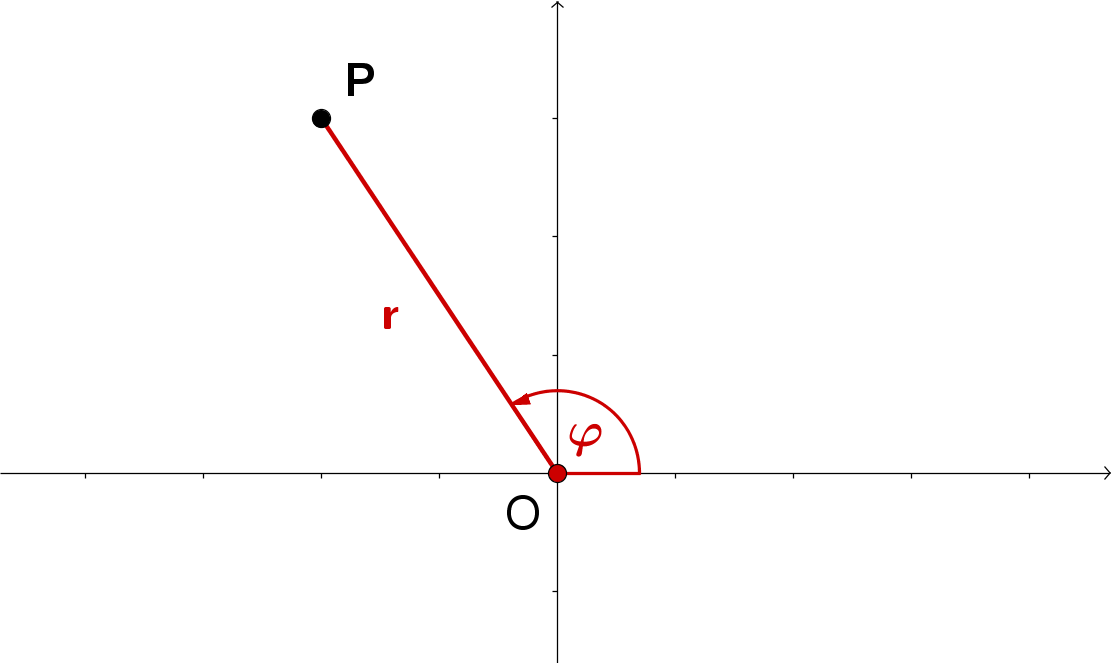
Der Punkt $P$ ist $5$ LE (Längeneinheiten) vom Koordinatenursprung entfernt und schließt mit der positiven x-Achse einen Winkel mit dem Maß $110 °$ ein.

Somit lauten seine Polarkoordinaten $(5 ∣ 110 °)$ .

Umrechnung

a) Polarkoordinaten $\rightarrow$ kartesische Koordinaten

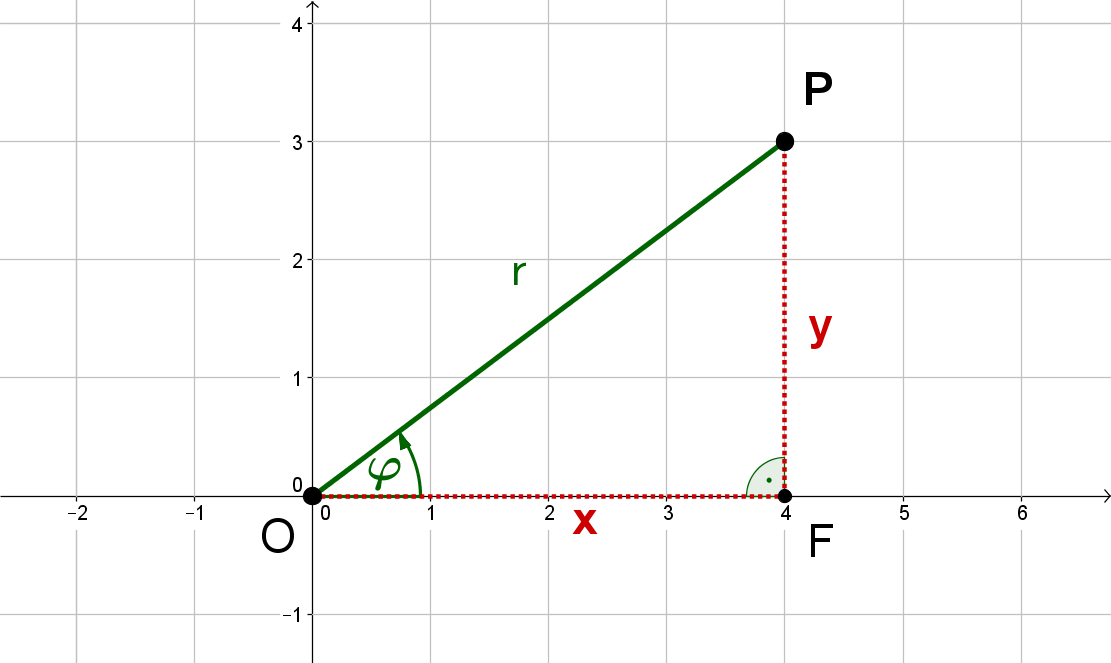
Man hat einen Punkt $P$ in Polarkoordinaten, also $(r|\varphi)$ , gegeben und möchte seine kartesischen Koordinaten berechnen.

Wendet man im rechtwinkligen Dreieck $\triangle OFP$ die Definition des Kosinus bzw. Sinus an, so ergibt sich

$\cos(\varphi)=\frac{x}{r}\,$ bzw. $\,\sin(\varphi)=\frac{y}{r}$ .

Multipliziert man beide Gleichungen jeweils mit $r$ , so ergibt sich:

\displaystyle x=r\cdot\cos(\varphi)

\displaystyle y=r\cdot\sin(\varphi)

b) Kartesische Koordinaten $\rightarrow$ Polarkoordinaten

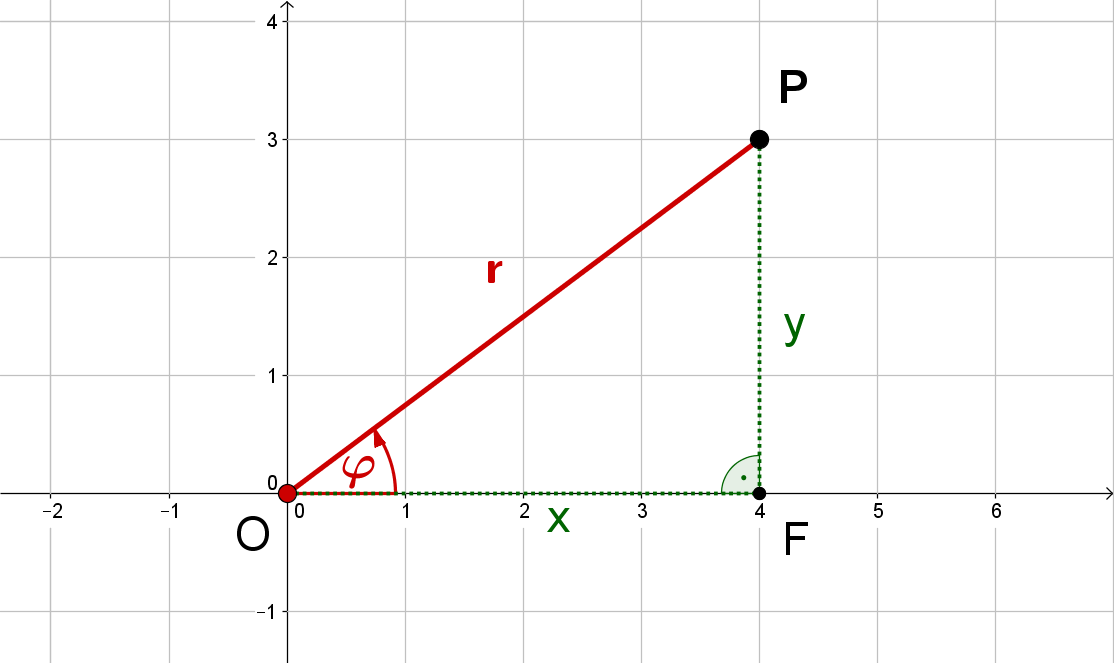
Man hat einen Punkt $P$ in kartesischen Koordinaten, also $(x ∣ y)$ , gegeben und möchte seine Polarkoordinaten berechnen.

Wendet man im rechtwinkligen Dreieck $\triangle OFP$ den Satz des Pythagoras an und zieht anschließend die Wurzel, so erhält man:

\displaystyle r=\sqrt{x^2+y^2}

Wendet man im selben Dreieck die Definition des Tangens und anschließend die inverse Funktion an, so erhält man:

\displaystyle \varphi=tan^{-1}\left(\frac{y}{x}\right)

Die letzte Beziehung ist allerdings nicht allgemeingültig, sondern muss ggf. noch modifiziert werden. Denn je nachdem, in welchem Quadranten der Punkt $P$ liegt, ergeben sich unterschiedliche Vorzeichen für $x$ bzw. $y$ . Daher ist die folgende Fallunterscheidung nötig:

\displaystyle x>0,y\ge0:\varphi=\tan^{-1}(\frac{y}{x})

\displaystyle x>0, y<0:\varphi=tan^{-1}(\frac{y}{x})+360°

\displaystyle x<0:\varphi=tan^{-1}(\frac{y}{x})+180°

Da die Gleichung außerdem für $x = 0$ nicht definiert ist ( $x$ -Koordinate im Nenner), muss dieser Fall gesondert betrachtet werden:

\displaystyle x=0, y>0:\,\varphi=90°

\displaystyle x=0, y=0:\,\varphi=0°

\displaystyle x=0, y<0:\,\varphi=270°

Beispielaufgabe

Der Punkt P hat die kartesischen Koordinaten $(- 4 ∣ 3)$ . Mit den obigen Formeln können seine Polarkoordinaten berechnet werden:

\displaystyle r=\sqrt{(-4)^2+3^2}=\sqrt{16+9}=\sqrt{25}=5

Da $x < 0$ ist, muss für die Berechnung von $\varphi$ die modifizierte Formel benutzt werden:

\displaystyle \varphi=tan^{-1}(\frac{3}{-4})+180°=tan^{-1}(-0{,}75)+180°\approx-36{,}87°+180°=143{,}13°

Der Punkt P hat somit $(5 ∣ 143,13 °)$ als Polarkoordinaten.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Polarkoordinaten

Umrechnung

a) Polarkoordinaten →\rightarrow→ kartesische Koordinaten

b) Kartesische Koordinaten →\rightarrow→ Polarkoordinaten

Beispielaufgabe

a) Polarkoordinaten $\rightarrow$ kartesische Koordinaten

b) Kartesische Koordinaten $\rightarrow$ Polarkoordinaten