Aufgaben zur Ableitung von Polynomfunktionen

Hier findest du Aufgaben, mit welchen du die Ableitung von Polynomfunktionen üben kannst.

1
Berechne die Ableitung der folgenden Polynomfunktionen.
1. $f (x) = x^{2} - 5$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung berechnen
  Du nimmst also für jeden Summanden die Hochzahl und setzt diese vor das $x$ . Anschließend verringerst du die Hochzahl um 1.
  $f^{'} (x) = {(x^{2} - 5)}^{'} = {(x^{2})}^{'} + {(- 5)}^{'} = 2 \cdot x^{2 - 1} + 0 = 2 x$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Es gilt: $(x^{n})^{'} = n \cdot x^{n - 1}$
  Außerdem gilt ${(u (x) + v (x))}^{'} = u^{'} (x) + v^{'} (x)$ und $(c \cdot u (x))^{'} = c \cdot u^{'} (x)$
2. $f (x) = 2 x^{2} + 4 x$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung berechnen
  $f^{'} (x) = {(2 x^{2} + 4 x)}^{'} = {(2 x^{2})}^{'} + {(4 x)}^{'} = 4 x + 4$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Es gilt: $(x^{n})^{'} = n \cdot x^{n - 1}$
  Außerdem gilt ${(u (x) + v (x))}^{'} = u^{'} (x) + v^{'} (x)$ und $(c \cdot u (x))^{'} = c \cdot u^{'} (x)$
3. $f (x) = 2 x^{5} - 3 x^{3} + x^{2} - 10$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung berechnen
  $f^{'} (x) = {(2 x^{5})}^{'} + {(- 3 x^{3})}^{'} + {(x^{2})}^{'} + {(- 10)}^{'} = 10 x^{4} - 9 x^{2} + 2 x$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Es gilt: $(x^{n})^{'} = n \cdot x^{n - 1}$
  Außerdem gilt ${(u (x) + v (x))}^{'} = u^{'} (x) + v^{'} (x)$ und $(c \cdot u (x))^{'} = c \cdot u^{'} (x)$
4. $f (x) = \frac{1}{2} x^{4} - 4 x^{3} + 6 x^{2} - 4 x + \frac{1}{8}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung berechnen
  $f^{'} (x) = {(\frac{1}{2} x^{4})}^{'} + {(- 4 x^{3})}^{'} + {(6 x^{2})}^{'} + {(- 4 x)}^{'} + {(\frac{1}{8})}^{'} = 2 x^{3} - 12 x^{2} + 12 x^{} - 4$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Es gilt: $(x^{n})^{'} = n \cdot x^{n - 1}$
  Außerdem gilt ${(u (x) + v (x))}^{'} = u^{'} (x) + v^{'} (x)$ und $(c \cdot u (x))^{'} = c \cdot u^{'} (x)$
5. $f (x) = \frac{1}{3} x^{3} - \frac{2}{5} x^{2} + 6 x$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung berechnen
  $f^{'} (x) = (\frac{1}{3} x^{3})^{'} - (\frac{2}{5} x^{2})^{'} + (6 x)^{'} = 3 \cdot \frac{1}{3} x^{2} - 2 \cdot \frac{2}{5} x + 6 = x^{2} - \frac{4}{5} x + 6$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Der Exponent jedes Summanden wird als Faktor vor das Ergebnis geschrieben und der neue Exponent ist der alte Exponent um 1 verringert.
6. $f (a) = 4 a^{4} - 3 a^{2} + 2$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung berechnen
  $f^{'} (a) = (4 a^{4} - 3 a^{2} + 2)^{'} = (4 a^{4})^{'} - (3 a^{2})^{'} + (2)^{'} = 16 a^{3} - 6 a$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Lass dich nicht davon verunsichern, dass das Funktionsargument in diesem Fall die Variable $a$ ist.
  Es gilt: $(a^{n})^{'} = n \cdot a^{n - 1}$
  Außerdem gilt ${(u (a) + v (a))}^{'} = u^{'} (a) + v^{'} (a)$ und $(c \cdot u (a))^{'} = c \cdot u^{'} (a)$
7. $f (x) = a x^{3} - b x + c$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung berechnen
  $f^{'} (x) = (a x^{3} - b x + c)^{'} = (a x^{3})^{'} - (b x)^{'} + (c)^{'} = 3 a x^{2} - b$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Variablen, die nicht das Funktionsargument (in diesem Fall x) sind, kannst du wie Zahlen behandeln.
  Es gilt: $(x^{n})^{'} = n \cdot x^{n - 1}$
  Außerdem gilt ${(u (x) + v (x))}^{'} = u^{'} (x) + v^{'} (x)$ und $(c \cdot u (x))^{'} = c \cdot u^{'} (x)$
8. $f (x) = 2 x^{5} - 10 x^{3} + 4 x^{2} + 1$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung berechnen
  $f^{'} (x) = {(2 x^{5} - 10 x^{3} + 4 x^{2} + 1)}^{'} = 2 \cdot 5 x^{5 - 1} - 10 \cdot 3 x^{3 - 1} + 4 \cdot 2 x^{2 - 1} = 10 x^{4} - 30 x^{2} + 8 x$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Es gilt: $(x^{n})^{'} = n \cdot x^{n - 1}$
  Außerdem gilt ${(u (x) + v (x))}^{'} = u^{'} (x) + v^{'} (x)$ und $(c \cdot u (x))^{'} = c \cdot u^{'} (x)$
9. $f (x) = \frac{1}{3} x^{6} - 3 x^{2} + 4 x + 5^{3}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung berechnen
  $f^{'} (x) = {(\frac{1}{3} x^{6} - 3 x^{2} + 4 x + 5^{3})}^{'} = 6 \cdot \frac{1}{3} \cdot x^{6 - 1} - 2 \cdot 3 \cdot x^{2 - 1} + 4 = 2 x^{5} - 6 x + 4$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Potenzen einfacher Zahlen sind Zahlen.
  Es gilt: $(x^{n})^{'} = n \cdot x^{n - 1}$
  Außerdem gilt ${(u (x) + v (x))}^{'} = u^{'} (x) + v^{'} (x)$ und $(c \cdot u (x))^{'} = c \cdot u^{'} (x)$
10. $x (t) = \frac{1}{2} a t^{2} + v_{0} t + x_{0}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung berechnen
  $x^{'} (t) = {(\frac{1}{2} a t^{2} + v_{0} t + x_{0})}^{'} = 2 \cdot \frac{1}{2} a t^{2 - 1} + v_{0} = a \cdot t + v_{0}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Lass dich nicht davon einschüchtern, dass Funktion $x$ und die Variable $t$ ist.
  Es gilt: $(t^{n})^{'} = n \cdot t^{n - 1}$
  Außerdem gilt ${(x (t) + y (t))}^{'} = x^{'} (t) + y^{'} (t)$ und $(c \cdot x (t))^{'} = c \cdot x^{'} (t)$
2
Ableitungspuzzle
Ziehe mit der Maus die entsprechenden Bilder zu den vorgegebenen Feldern.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Zu der Funktion
$f (x) = 2 x^{4} - 4 x^{2} - 3$
gehört der nebenstehende Graph.
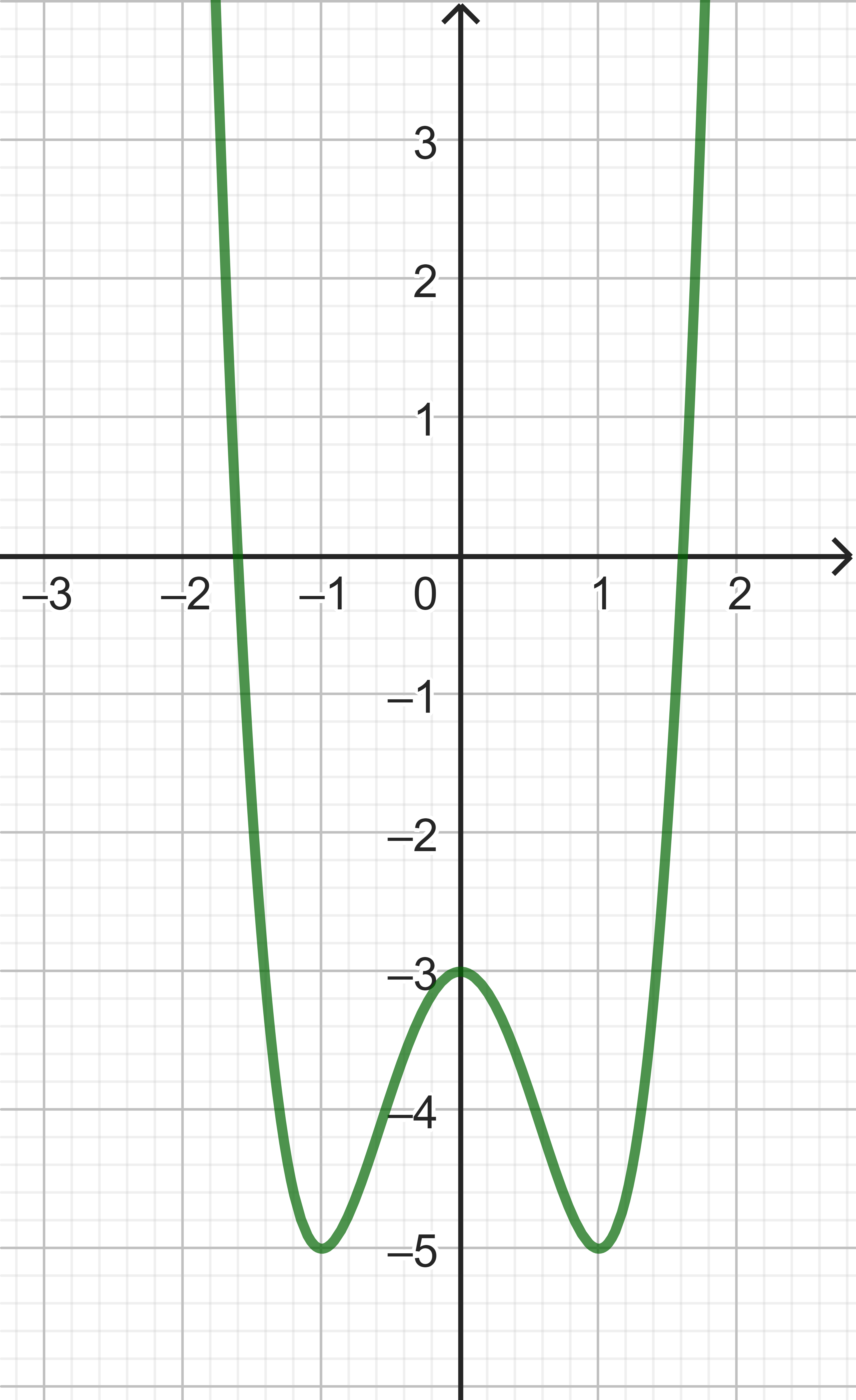
Mit den Ableitungsregeln folgt für die
1. Ableitung:
$f^{'} (x) = 8 x^{3} - 8 x$
Der zugehörige Graph ist hier abgebildet.
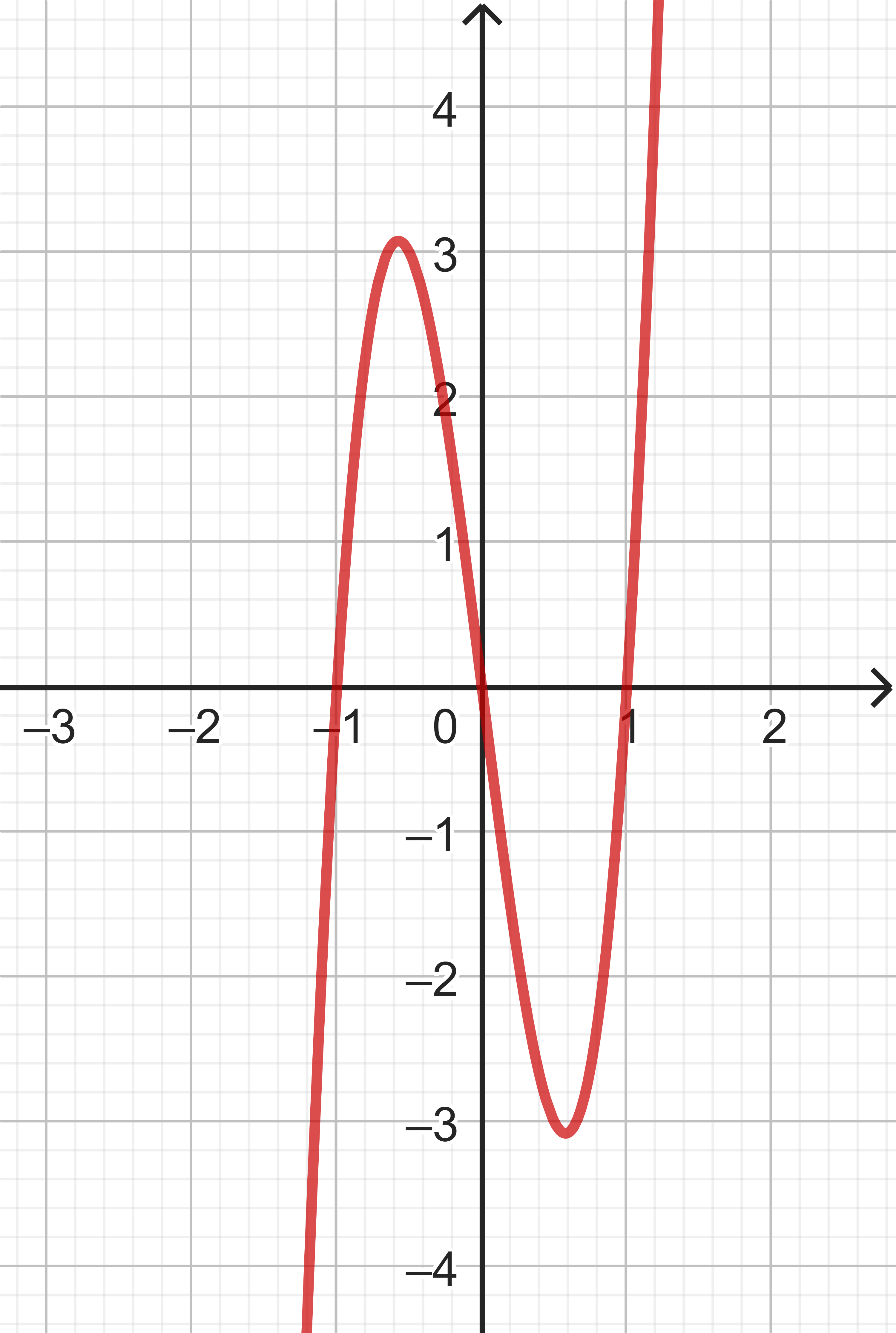
Für die 2. Ableitung folgt:
$f^{''} (x) = 24 x^{2} - 8$
Der zugehörige Graph ist nebenstehend abgebildet.

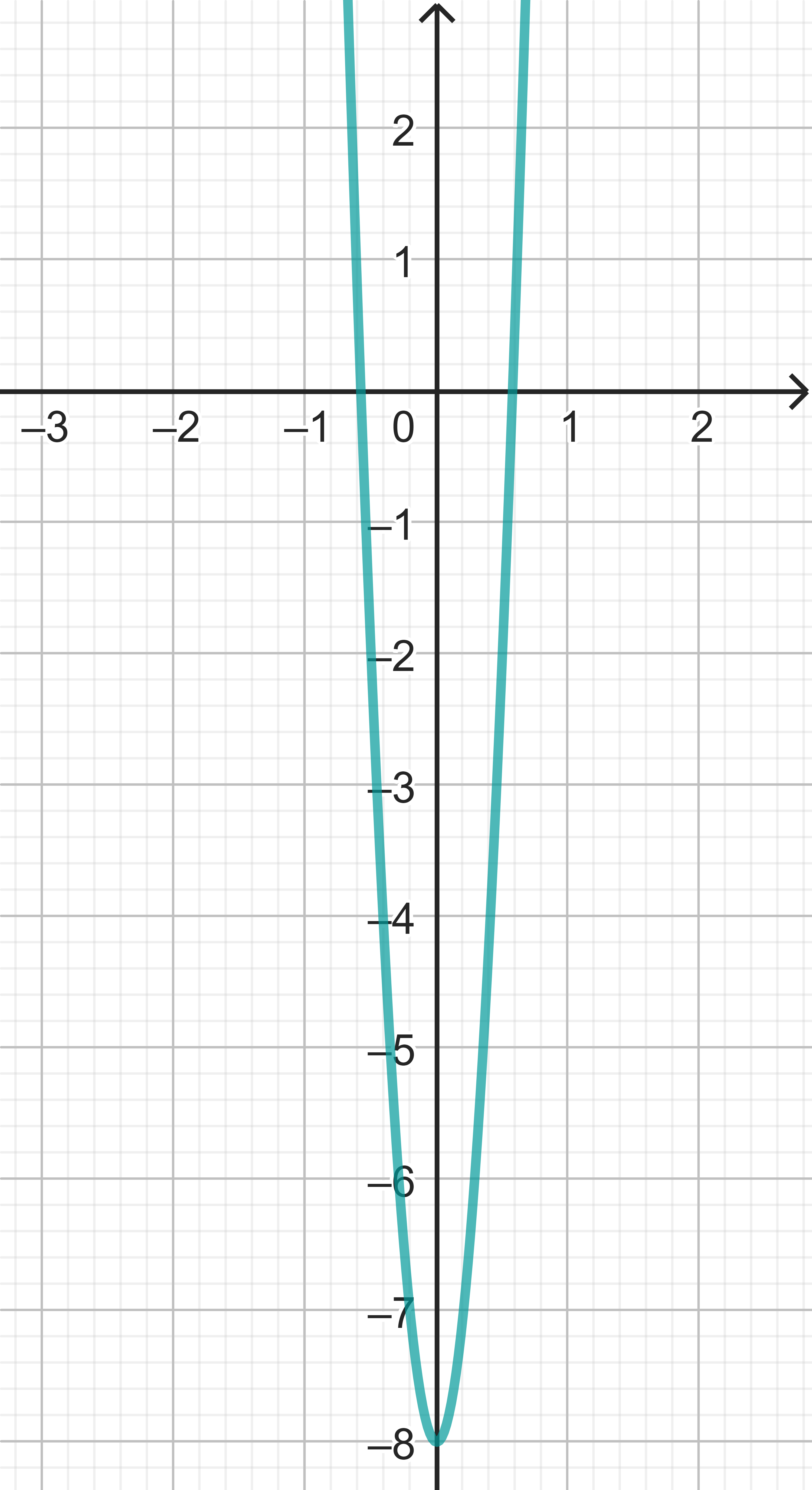
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Aufgaben zur Ableitung von Polynomfunktionen

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?