Das Planungsbüro stellt der Projektleitung eine mögliche Gleisverbindung mit einer Funktion 3. Grades vor. Das Ergebnis ist in Abbildung 1 dargestellt.
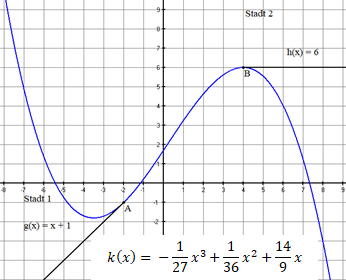
Abb.1: Verbindung der Bahnhöfe mit einer kubischen Funktion k(x)
Ein Mitarbeiter der Projektleitung bemängelt die fehlende „Krümmungsruckfreiheit“ an den Übergangspunkten. Er weiß aus Erfahrung, dass eine Funktion 3. Grades nie an zwei Punkten gleichzeitig krümmungsruckfrei sein kann.
Teilaufgabe 1. Zeige allgemein, dass er Recht hat.
Teilaufgabe 2. Weise dies auch rechnerisch für die angegebene Funktion k(x) und die Punkte A und B nach.
Lösung Teilaufgabe b1)
Allgemeiner Ansatz für eine Funktion 3. Grades: k(x)=ax3+bx2+cx+d
Die erste Ableitung von k(x) lautet: k′(x)=3ax2+2bx+c
Die zweite Ableitung von k(x) lautet: k′′(x)=6ax+2b
Für einen Wendepunkt muss die 2. Ableitung gleich Null sein:
0=6ax+2b⇒x=−6a2b=−3ab
Somit gibt es nur eine Wendestelle, d.h. es kann nur an einem Punkt ein krümmungsruckfreier Übergang stattfinden und nicht an zwei Punkten.
Der Mitarbeiter der Projektleitung hat Recht.
Lösung Teilaufgabe b2)
Die angegebene Funktion k(x) lautet:
k(x)=−271x3+361x2+914x+2746
k′(x)=−91x2+181x+914
k′′(x)=−92x+181
Für den Punkt A(−2−1) gilt: k′′(−2)=94+181=21 und g′′(−2)=0
d.h. k′′(−2)=g′′(−2).
Für den Punkt B(4∣6) gilt: k′′(4)=−98+181=−1815 und h′′(4)=0
d.h. k′′(4)=h′′(4).
Somit gibt es an beiden Punkten einen Krümmungsruck.
Das Planungsbüro der Bundesbahn hat nun eine Funktion 5. Grades berechnet, die den Gleisverlauf beschreibt:
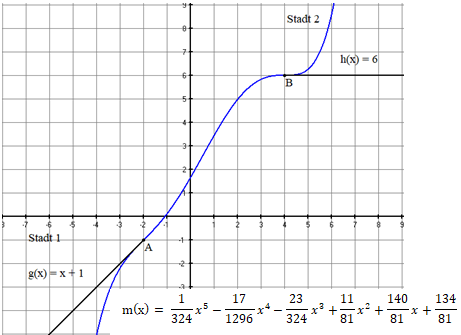
Abb.2 Graph der Funktion m(x).
Erläutere anhand der Abbildung 2, dass die Krümmungsruckfreiheit im Punkt B erfüllt ist.
Zeige rechnerisch, dass auch im Punkt A ein krümmungsruckfreier Übergang möglich ist.
Lösung Teilaufgabe c1)
Die Abbildung 2 zeigt, dass die Funktion 5. Grades im Punkt B(4∣6) einen Sattelpunkt hat, d.h. die zweite Ableitung der Funktion m(x) ist hier gleich Null.
