Linearkombinationen, Gleichungssysteme und Matrizen

Hier werden die Zusammenhänge von Linearkombinationen, (linearen) Gleichungssysteme und Matrizen gezeigt.

Das Ziel ist es, zu verstehen, wieso ein lineares Gleichungssystem (siehe Bild) geschrieben werden kann als Matrix.

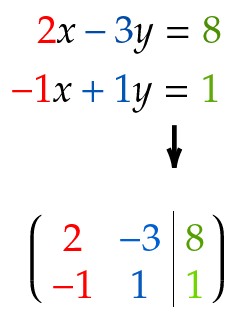
Ein Beispiel für ein lineares Gleichungssystem. Das kann auch mit einer Matrix geschrieben werden.

Wenn hier den Begriff Gleichungssystem oder auch einfach nur System verwendet wird, ist immer ein lineares Gleichungssystem gemeint.

Linearkombinationen und Gleichungssysteme

Wir beginnen mit einem Gleichungssystem:

$\def\arraystretch{1.25} \begin{array}{rcrc} 2x&+&3y&=8\\ -x&+&y&=1 \end{array}$

Die Frage ist:

welche beiden Zahlen $x$ und $y$ erfüllen beide Zeilen gleichzeitig?

Das kannst du mit einem der bekannten Verfahren wie Additionsverfahren oder Gaußverfahren berechnen. Die Lösung ist übrigens $\color{green}x=1$ und $\color{green} y=2$ .

Als nächstes schreiben wir das Systems in Vektoren um und wenden die Rechenregeln an:

$\begin{pmatrix} 2x+3y\\-x+y\end{pmatrix}=\begin{pmatrix}8\\1 \end{pmatrix} \iff \begin{pmatrix} 2x\\-x\end{pmatrix}+\begin{pmatrix} 3y\\y\end{pmatrix}=\begin{pmatrix}8\\1 \end{pmatrix}\iff x\begin{pmatrix} 2\\-1\end{pmatrix}+y\begin{pmatrix} 3\\1\end{pmatrix}=\begin{pmatrix}8\\1 \end{pmatrix}$

Jetzt ist die Frage:

Welche Koeffizienten $x$ und $y$ braucht man, um den Vektor $\begin{pmatrix}8\\1 \end{pmatrix}$ als Linearkombination von $\begin{pmatrix}2\\-1 \end{pmatrix}$ und $\begin{pmatrix}3\\1 \end{pmatrix}$ darzustellen?

Merke

Das Gleichungssystem $\def\arraystretch{1.25} \begin{array}{ccc} a_{11}\, x +a_{12}\,y+a_{13}\,z&=&b_1\\ a_{21}\, x +a_{22}\,y+a_{23}\,z&=&b_2\\ a_{31}\, x +a_{32}\,y+a_{33}\,z&=&b_3 \end{array}$ und das Problem

"Welche Koeffizienten $x$ , $y$ und $z$ braucht man, damit die Linearkombination

$x\cdot\begin{pmatrix}a_{11}\\a_{21}\\a_{31}\end{pmatrix} + y\cdot\begin{pmatrix}a_{12}\\a_{22}\\a_{32}\end{pmatrix} + z\cdot\begin{pmatrix}a_{13}\\a_{23}\\a_{33}\end{pmatrix}$ den Vektor $\begin{pmatrix}b_1\\b_2\\b_3 \end{pmatrix}$ ergibt?"

haben die selben Lösungen. Es sind verschiedene Schreibweisen desselben Sachverhalts.

Linearkombinationen und Matrizen

Sicher hast du schon gesehen, wie man eine Matrix mit einem Vektor multipliziert:

Ist $A=\begin{pmatrix}a&b\\c&d \end{pmatrix}$ und $\vec{v}=\begin{pmatrix}r\\s \end{pmatrix}$ , dann ist $A\cdot \vec{v}=\begin{pmatrix}a\cdot r+b\cdot s \\c\cdot r+d\cdot s\end{pmatrix}$ .

Das ist vollkommen richtig und hilfreich beim konkreten Berechnen, aber für das Verstehen formt man das noch mal um:

$A\cdot \vec{v}=\begin{pmatrix}a\cdot r+b\cdot s \\c\cdot r+d\cdot s\end{pmatrix}=\underbrace{r\cdot\begin{pmatrix}a\\c \end{pmatrix}+s\cdot\begin{pmatrix}b\\d \end{pmatrix}}_{\text{Linearkombination der Spalten der Matrix}}$

Unser Beispiel lässt sich deshalb so umformen:

\displaystyle x\begin{pmatrix} 2\\-1\end{pmatrix}+y\begin{pmatrix} 3\\1\end{pmatrix}=\begin{pmatrix}8\\1 \end{pmatrix}\iff \begin{pmatrix} ~~2 ~~~~~ 3\\-1~~~~1\end{pmatrix}\cdot\begin{pmatrix}x\\y \end{pmatrix}=\begin{pmatrix}8\\1 \end{pmatrix}

Daher stellst du fest:

MerkeProdukt von Matrix und Vektor

Ist $A=\begin{pmatrix}|&|&|\\\vec{a}_1&\vec{a}_2&\vec{a}_3\\|&|& |\end{pmatrix}$ eine Matrix und $\vec{v}= \begin{pmatrix}v_1\\v_2\\v_3 \end{pmatrix}$ ein Vektor, so ist das Produkt $A\cdot\vec{v}$ eine Linearkombination der Spalten von $A$ mit den Koeffizienten der Einträge von $\vec{v}:$

\displaystyle A\cdot\vec{v}=v_1\,\vec{a}_1+v_2\,\vec{a}_2+v_3\,\vec{a}_3

Dabei siehst du noch einmal zwei Dinge:

Es ist sinnvoll, die Matrix $A$ nicht nur als rechteckiges Schema zu betrachten, sondern als Anreihung von (Spalten-)Vektoren.
Ein Produkt $A\cdot\vec{v}$ kannst du genau dann bilden, wenn die Spaltenzahl von $A$ gleich der Zahl der Einträge in $\vec{v}$ ist.

Die Frage: welche Linearkombination der Vektoren $\vec{a}_1$ und $\vec{a}_2$ ergibt den Vektor $\vec{b}$ , also:

Wie muss ich $v_{1}$ und $v_{2}$ in der Gleichung $v_1\,\vec{a}_1+v_2\,\vec{a}_2=\vec{b}$ wählen?

kann auch so formuliert werden:

Welcher Vektor $\vec{v}=\begin{pmatrix}v_1\\v_2 \end{pmatrix}$ löst die Matrix-Vektor-Gleichung $A\cdot\vec{v}=\vec{b}$ ,? Dabei ist $A$ eine Matrix mit den Spalten $\vec{a}_1$ und $\vec{a}_2$ .

Gleichungssysteme und Matrizen

Jetzt kannst du die Abschnitte über Gleichungssysteme, Linearkombinationen und Matrizen einfach zusammenfassen:

Das Gleichungssystem ganz am Anfang

\displaystyle \def\arraystretch{1.25} \begin{array}{rcrc} 2x&+&3y&=8\\ -x&+&y&=1 \end{array}

schreibt sich jetzt als erweiterte Matrix

\displaystyle \def\arraystretch{1.25} \left(\begin{array}{cc|c} 2&3&8\\ -1&1&1 \end{array}\right)

und der Vektor $\vec{v}=\begin{pmatrix}x\\y \end{pmatrix}$ ist die Lösung der Gleichung

MerkeAllgemein

Das Gleichungssystem

\displaystyle \def\arraystretch{1.25} \begin{array}{ccc} a_{11}\, x +a_{12}\,y+a_{13}\,z&=&b_1\\ a_{21}\, x +a_{22}\,y+a_{23}\,z&=&b_2\\ a_{31}\, x +a_{32}\,y+a_{33}\,z&=&b_3 \end{array}

ist äquivalent zu diesem Problem mit den Matrizen:

Ist $A=\begin{pmatrix} a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{33} \end{pmatrix}$ und $\vec{b}=\begin{pmatrix} b_1 \\b_2\\b_3\end{pmatrix}$ , so ist der Vektor $\vec{u}=\begin{pmatrix}x\\y\\z \end{pmatrix}$ die Lösung von

\displaystyle A\cdot\vec{u}=\vec{b}

In Worten: Mit welchem Vektor $\vec{u}$ muss man $A$ multiplizieren, um $\vec{b}$ zu erhalten?

Umgekehrt kann die Lösung $\vec{u}$ von $A\cdot\vec{u}=\vec{b}$ durch das Lösen des Gleichungssystems bestimmt werden.

Das führt zu folgender Schreibweise

Erweiterte Matrix

Das Gleichungssystem in der Box oben schreibst du in der Form

\displaystyle \def\arraystretch{1.25} \left(\begin{array}{ccc|c} a_{11}&a_{12}&a_{13}&b_1\\ a_{21}&a_{22}&a_{23}&b_2\\ a_{31}&a_{32}&a_{33}&b_3 \end{array}\right)

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?