Setze die Nullstellen der 1. Ableitung in die 2. Ableitung ein, um die Art des Extrempunktes zu bestimmen, also ob es sich um einen Hochpunkt oder Tiefpunkt handelt.
Aber Achtung: Hat die 2. Ableitung an dieser Stelle ebenfalls eine Nullstelle, kannst du durch diese Methode weder nachweisen, ob es sich um eine Extremstelle handelt, noch, welche Art diese hat!
Du hast bereits die Nullstellen der 1. Ableitung bestimmt und so Kandidaten für die Extremstellen eines Graphen ermittelt?
Setze diese in die 2. Ableitung ein.
Der Graph hat einen Hochpunkt bei , wenn gilt:
( ist Nullstelle der Ableitung)
(Graph ist rechtsgekrümmt)
Der Graph hat einen Tiefpunkt bei , wenn gilt:
( ist Nullstelle der Ableitung)
(Graph ist linksgekrümmt)
Gilt , so kann mit dieser Methode keine Entscheidung getroffen werden.
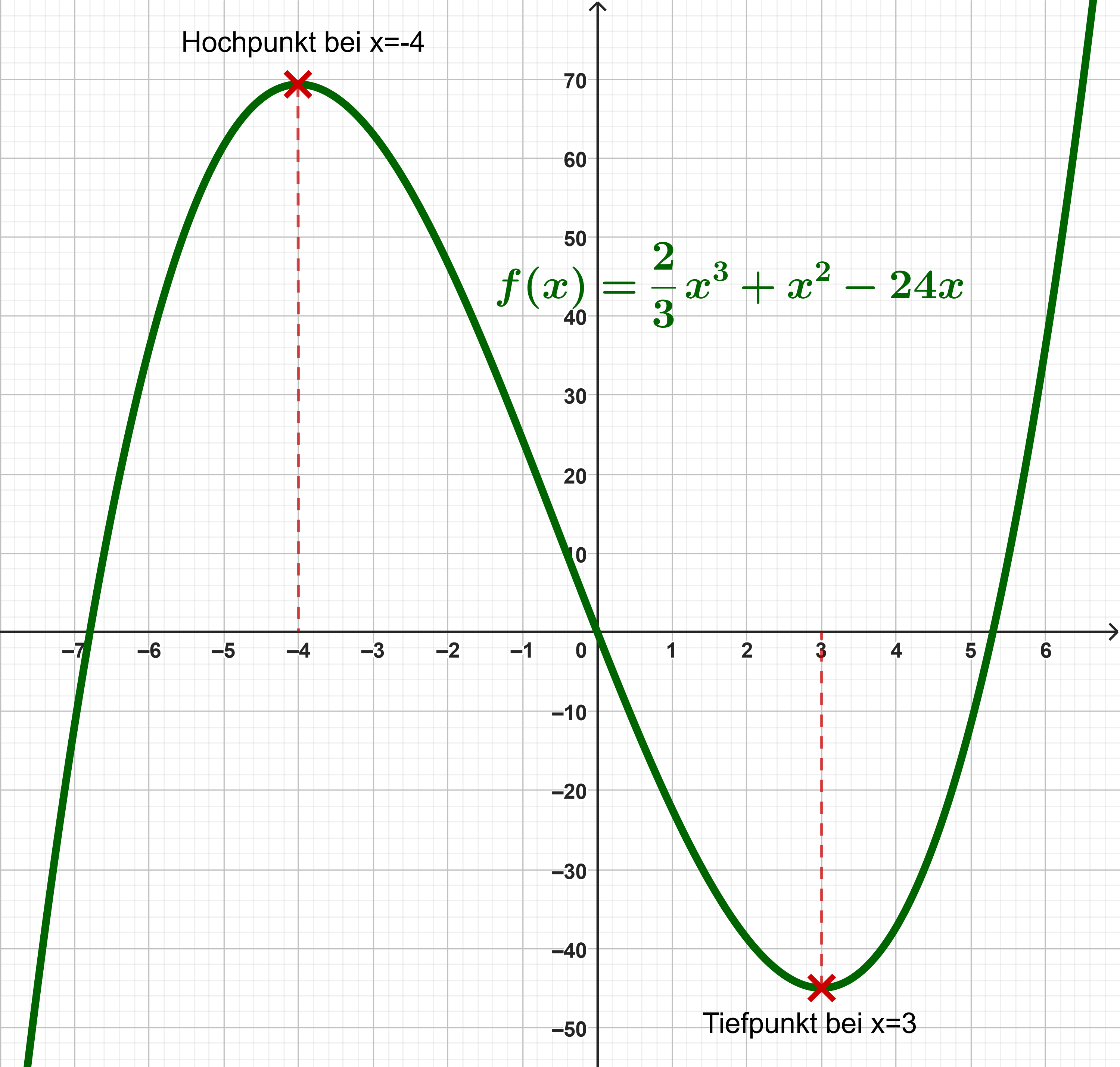
Erklärung am Beispiel
Gesucht werden die Extremstellen der Funktion .
Die 1. Ableitung lautet:
Die Gleichung
wird durch die Stellen und gelöst, was durch die Mitternachtsformel, pq-Formel oder den Satz von Vieta bestimmt werden kann. Das sind also mögliche Kandidaten für Extremstellen.
Bestimmen der Art der Extremstelle
Die 2. Ableitung der Funktion lautet:
Die erste Stelle eingesetzt ergibt:
Hier liegt ein Hochpunkt vor.
Die zweite Stelle eingesetzt ergibt:
Damit liegt ein Tiefpunkt vor.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
