Aufgabe A 3
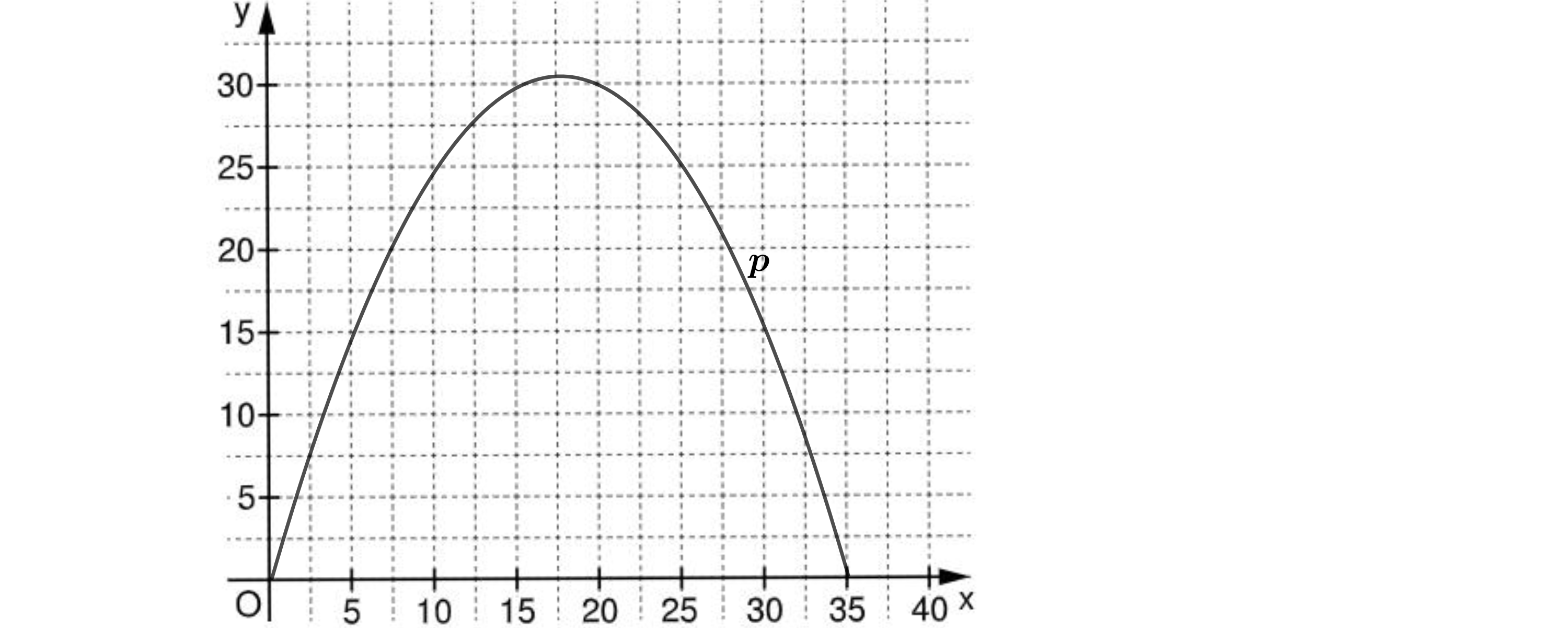
Ein Floh kann bezogen auf seine Körpergröße sehr weit und sehr hoch springen. Ein solcher Sprung kann näherungsweise durch die Parabel ,
beschrieben werden. Dabei entspricht der horizontal gemessenen Entfernung vom Absprungpunkt und der zugehörigen Höhe über dem Boden. Der Floh landet im Punkt auf dem Boden.
Berechnen Sie die Koordinaten des Scheitelpunkts der Parabel . Zeichnen Sie sodann die Parabel für in das Koordinatensystem ein. (3 P)
Geben Sie die maximale Höhe und die Weite dieses Sprungs an.
Runden Sie auf ganze Zentimeter. (1 P)
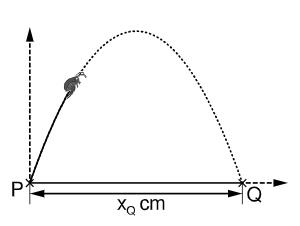
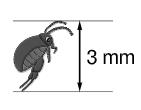
Der unten abgebildete Floh kann bis zu weit springen. Kreuzen Sie an, wie weit ein großer Mensch ungefähr springen würde, wenn er im Verhältnis zu seiner Körpergröße genauso weit wie dieser Floh springen könnte.
Kreuze die entsprechende Antwort an. (1 P)