Aufgabe B 1
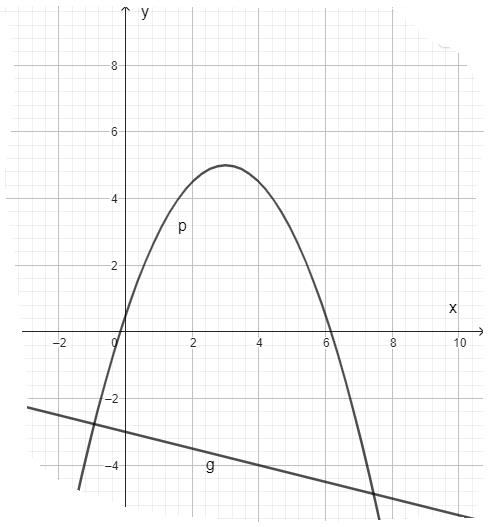
Die Parabel mit dem Scheitelpunkt hat eine Gleichung der Form
mit und .
Die Gerade hat die Gleichung mit
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
Zeigen Sie rechnerisch, dass die Parabel die Gleichung hat. Zeichnen Sie sodann die Parabel und die Gerade für in ein Koordinatensystem ein. (3 P)
Für die Zeichnung: Längeneinheit ; ;
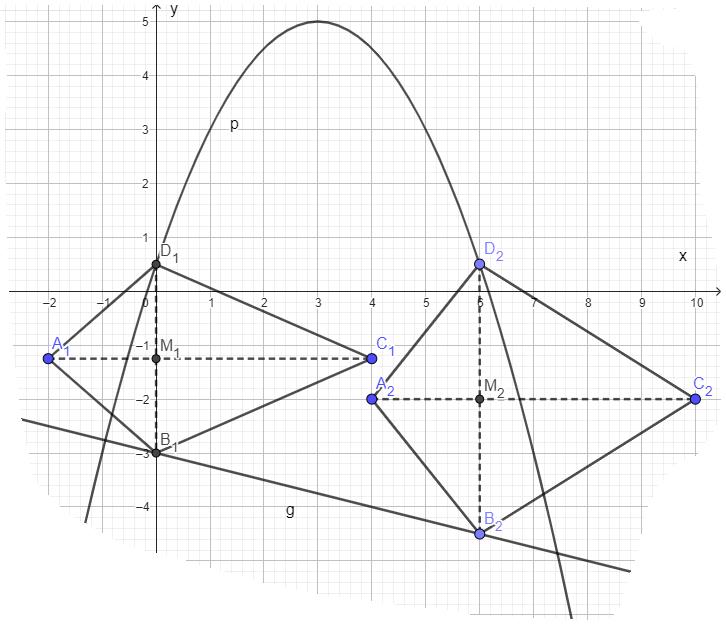
Punkte auf der Geraden und Punkte auf der Parabel haben dieselbe Abszisse . Sie sind zusammen mit Punkten und Eckpunkte von Drachenvierecken mit den Symmetrieachsen und den Diagonalenschnittpunkten .
Es gilt: ; ; .
Zeichnen Sie das Drachenviereck für und das Drachenviereck für in das Koordinatensystem zu 1a) ein. (2 P)
Begründen Sie, weshalb der Flächeninhalt der Dreiecke stets halb so groß wie der Flächeninhalt der Dreiecke ist. (1 P)
Ermitteln Sie rechnerisch, für welche Werte von es Drachenvierecke gibt. (3 P)
Unter den Drachenvierecken hat das Drachenviereck den maximalen Flächeninhalt.
Berechnen Sie diesen Flächeninhalt und den zugehörigen Wert für . (4 P)
Zwischenergebnis:
Unter den Drachenvierecken gibt es zwei Drachenvierecke und , die bei bzw. rechtwinklig sind.
Begründen Sie, warum gilt.
Berechnen Sie sodann die -Koordinaten von und (3 P)