Geometrie, Teil A, Aufgabengruppe 2

A liegt auf g?

Erstelle die Gleichung der Geraden $g$:

Wähle als Aufpunkt den Punkt $B(1|1|1)$ und den Richtungsvektor $\begin{pmatrix} 1 \\ 2 \\ 2 \end{pmatrix}$.

$g:\;\vec X=\begin{pmatrix}1\\1\\1\end{pmatrix} +r\cdot \begin{pmatrix} 1 \\ 2 \\ 2 \end{pmatrix}$

Führe eine Punktprobe durch. Setze für $\vec X$ den Vektor $\vec A$ ein.

$\begin{pmatrix}3\\5\\5\end{pmatrix}=\begin{pmatrix}1\\1\\1\end{pmatrix}+r\cdot\begin{pmatrix}1\\2\\2\end{pmatrix}\;\Rightarrow\;\begin{pmatrix}2\\4\\4\end{pmatrix}=r\cdot\begin{pmatrix}1\\2\\2\end{pmatrix}$

Du hast ein Gleichungssystem mit drei Gleichungen und einer Unbekannten erhalten.

$\mathrm{(I)}\;\;\; 2=r\\\mathrm{(II)}\;\; 4=2r\;\Rightarrow\;r=2\\\mathrm{(III)}\; 4=2r\;\Rightarrow\;r=2$

Damit hat das Gleichungssystem die Lösung $r=2$ und der Punkt $A$ liegt auf $g$.

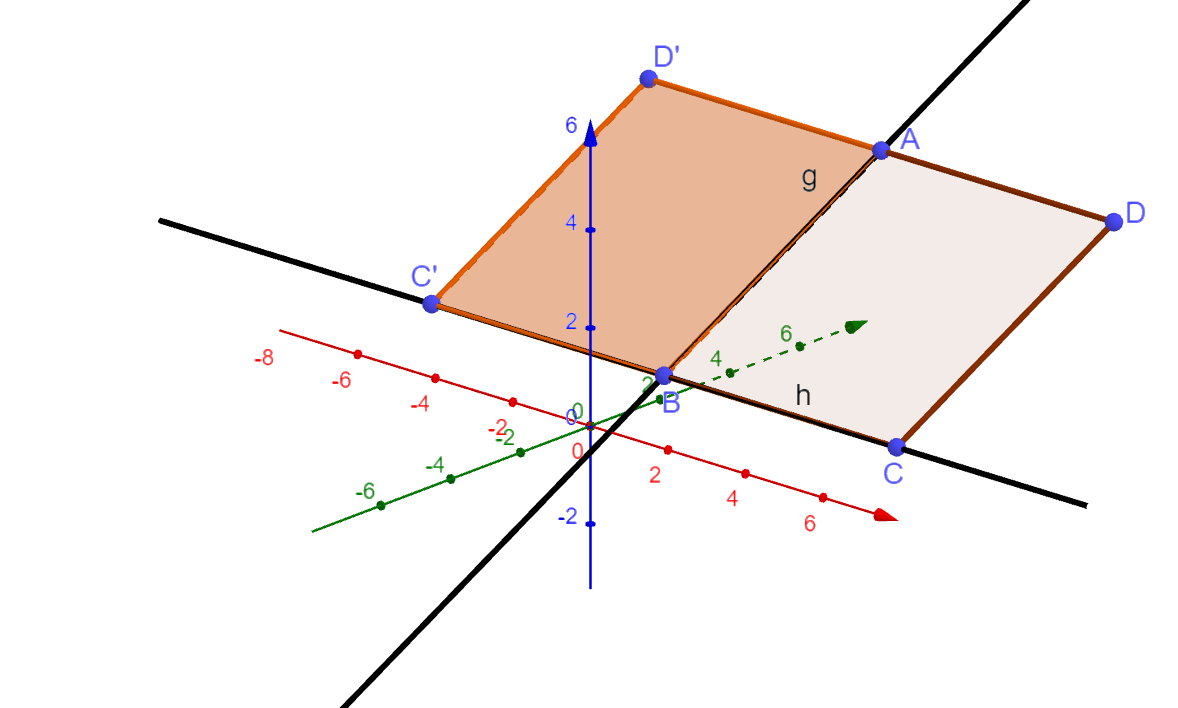
Bei einer Raute sind die Seiten gleichlang und die gegenüberliegenden Seiten sind parallel zueinander.

Erstelle die Gleichung der Geraden $h$:

Wähle als Aufpunkt den Punkt $B(1|1|1)$ und den Richtungsvektor $\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}$.

$h:\;\vec X=\begin{pmatrix}1\\1\\1\end{pmatrix} +s\cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}$

Berechne die Länge der Seite $|\overline{BA}|$:

$\overrightarrow{BA}=\begin{pmatrix}3\\5\\5\end{pmatrix}-\begin{pmatrix}1\\1\\1\end{pmatrix}=\begin{pmatrix}2\\4\\4\end{pmatrix}$

$\Big|\overrightarrow{BA}\Big|=\sqrt{2^2+4^2+4^2}=\sqrt{36}=6\;\text{LE}$

Da es sich um eine Raute handelt, muss auch die Seite $|\overline{BC}|\; 6 \;\text{LE}$ lang sein.

Der Punkt $C$ liegt auf der Geraden $h\;\Rightarrow\;\vec C=\begin{pmatrix}1\\1\\1\end{pmatrix} +s\cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}$

Der Richtungsvektor der Geraden $h$ ist ein Einheitsvektor, d.h. er muss genau sechsmal (wegen der Länge $6 \;\text{LE}$) zum Vektor $\vec B$ addiert werden, um zum Vektor $\vec C$ zu gelangen.

$\Rightarrow\;\vec C=\begin{pmatrix}1\\1\\1\end{pmatrix} +6\cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}=\begin{pmatrix}7\\1\\1\end{pmatrix}$

Der Punkt $C$ hat die Koordinaten $C(7|1|1)$.

Einen weiteren Punkt $C'$ findet man, wenn der Einheitsvektor sechsmal vom Vektor $\vec B$ subtrahiert wird.

$\Rightarrow\;\vec C'=\begin{pmatrix}1\\1\\1\end{pmatrix} -6\cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}=\begin{pmatrix}-5\\1\\1\end{pmatrix}$

Der Punkt $C'$ hat die Koordinaten $C(-5|1|1)$.

Entsprechend erhält man auch die Koordinaten des Punktes $D$.

Hier gilt:

$\vec D=\vec A+6\cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}=\begin{pmatrix}3\\5\\5\end{pmatrix}+6\cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}=\begin{pmatrix}9\\5\\5\end{pmatrix}$

Der Punkt $D$ hat die Koordinaten $D(9|5|5)$.

Einen weiteren Punkt $D'$ findet man, wenn der Einheitsvektor sechsmal vom Vektor $\vec A$ subtrahiert wird.

$\Rightarrow\;\vec D'=\begin{pmatrix}3\\5\\5\end{pmatrix} -6\cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}=\begin{pmatrix}-3\\5\\5\end{pmatrix}$

Der Punkt $D'$ hat die Koordinaten $D'(-3|5|5)$.

Die Punkte $A$, $B$, $C$ und $D$ bilden eine Raute.

Die Punkte $A$, $B$, $C'$ und $D'$ bilden ebenfalls eine Raute.

Die folgende Abbildung wurde nicht in der Aufgabenstellung verlangt.

Sie dient nur der Veranschaulichung.