Ein Kreis ist eine runde geometrische Form, wie sie in den Bildern zu sehen ist.
Das sind die wichtigen Begriffe zum Kreis:

Die Bilder zeigen Kreise, die du aus dem Alltag kennst: Uhren, Kekse, Räder und Hula Hoop - Reifen.
Was ist ein Kreis?
Nicht jede runde Figur ist ein Kreis.
Ein Beispiel dafür: die Ellipse

Im Bild ist ein Kreisbogen.
Das ist kein vollständiger Kreis.

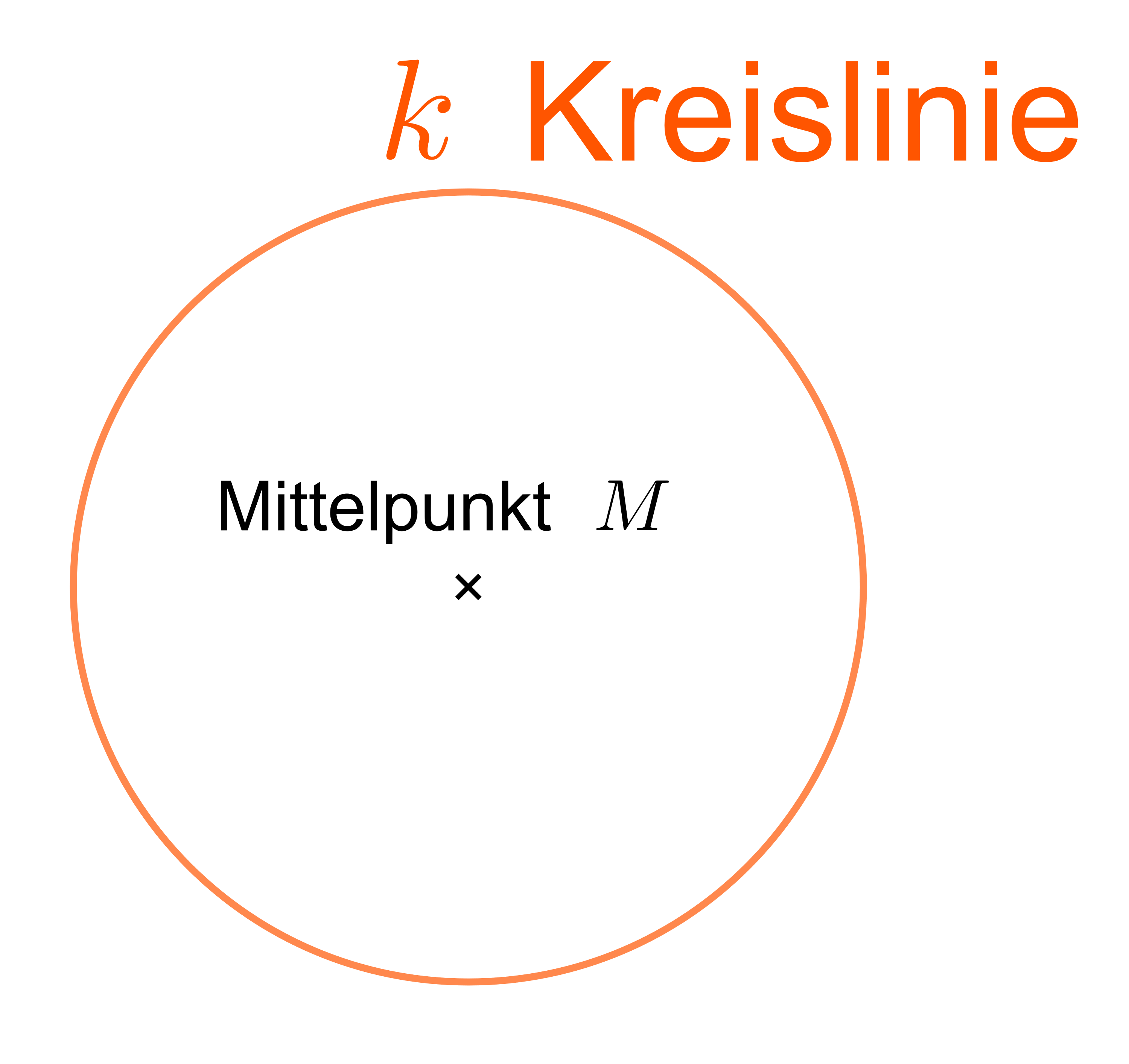
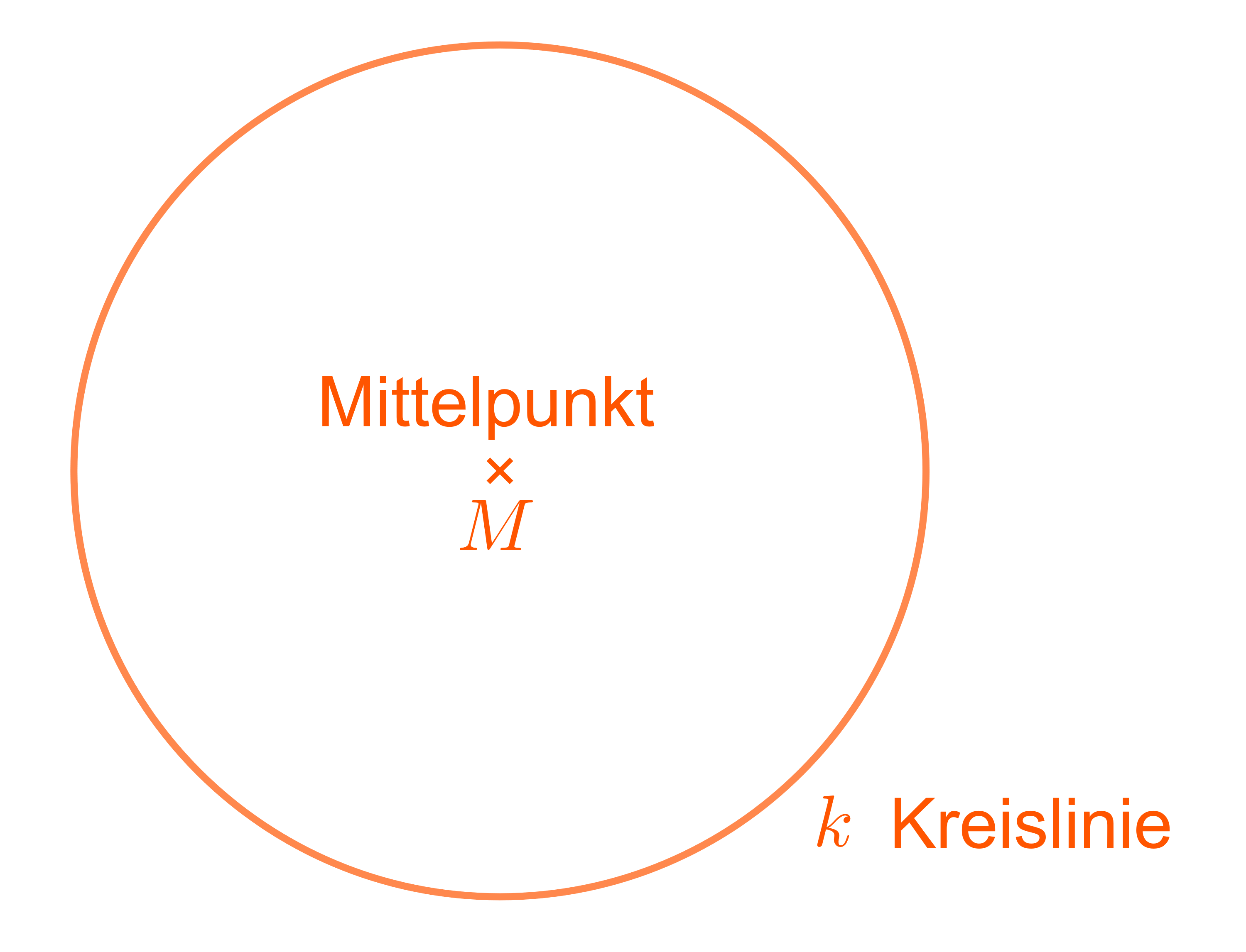
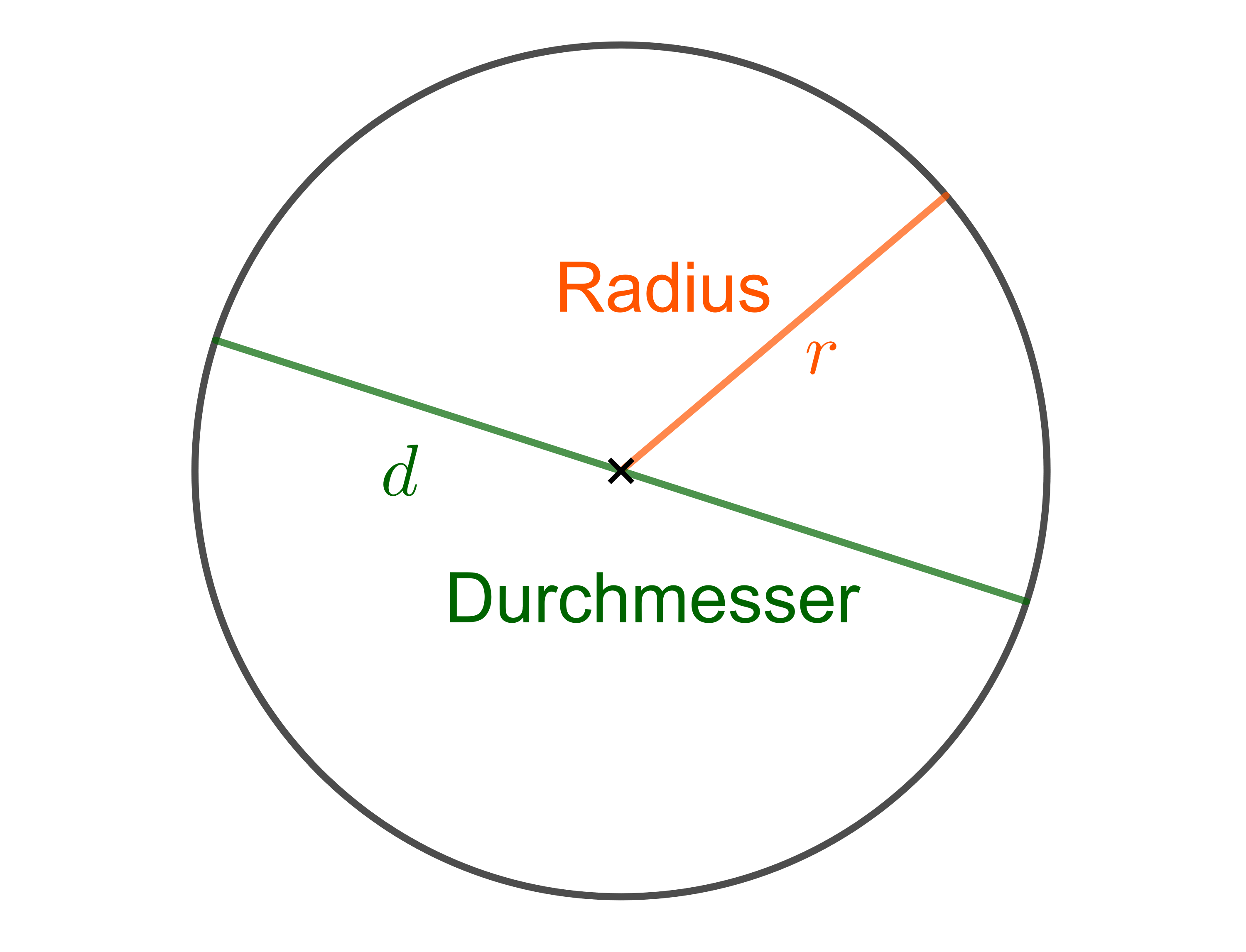
Kreislinie, Radius, Durchmesser und Mittelpunkt
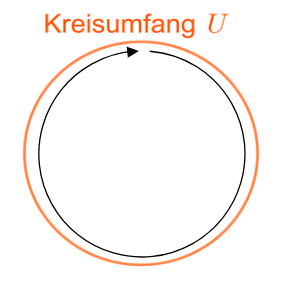
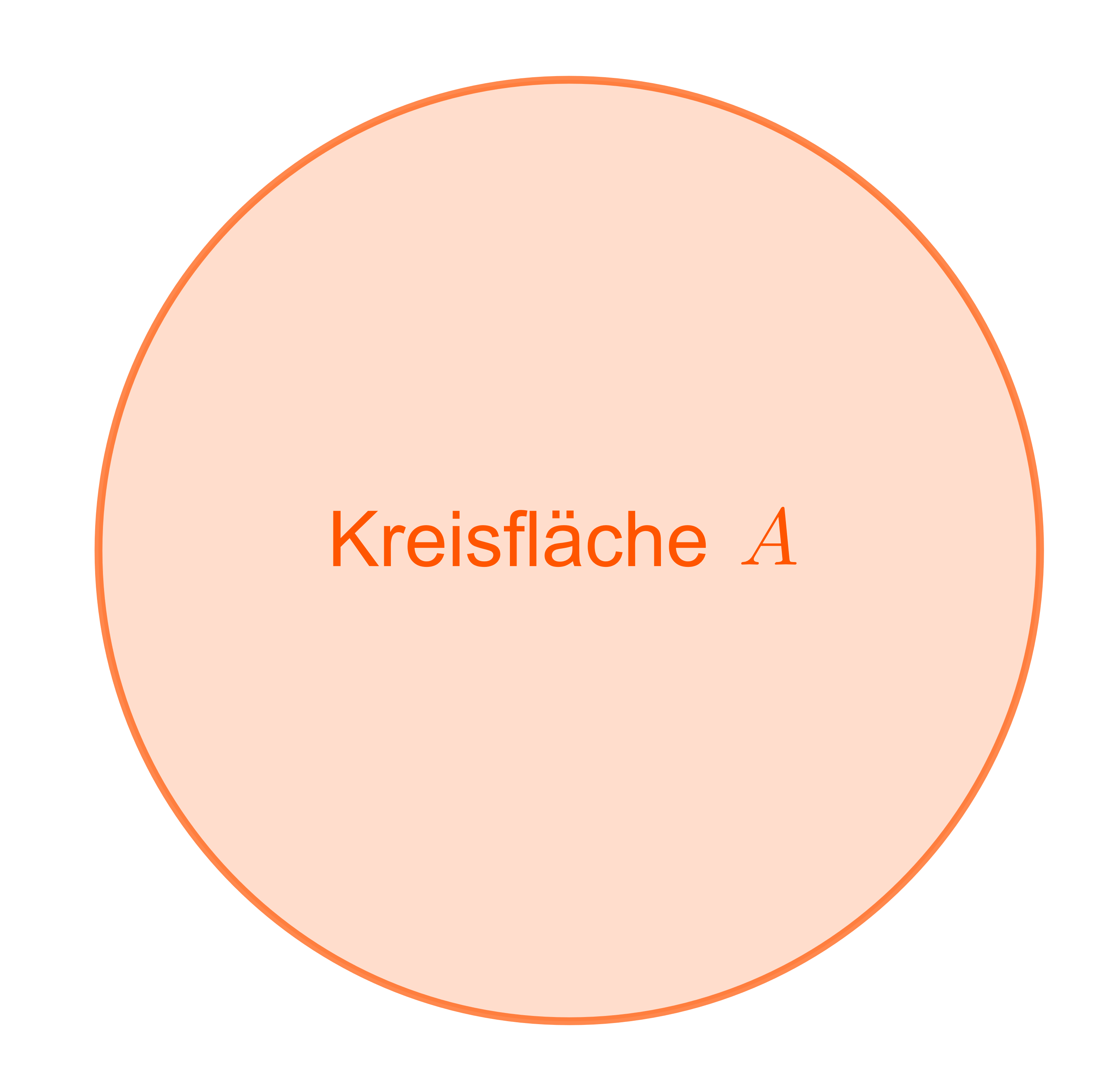
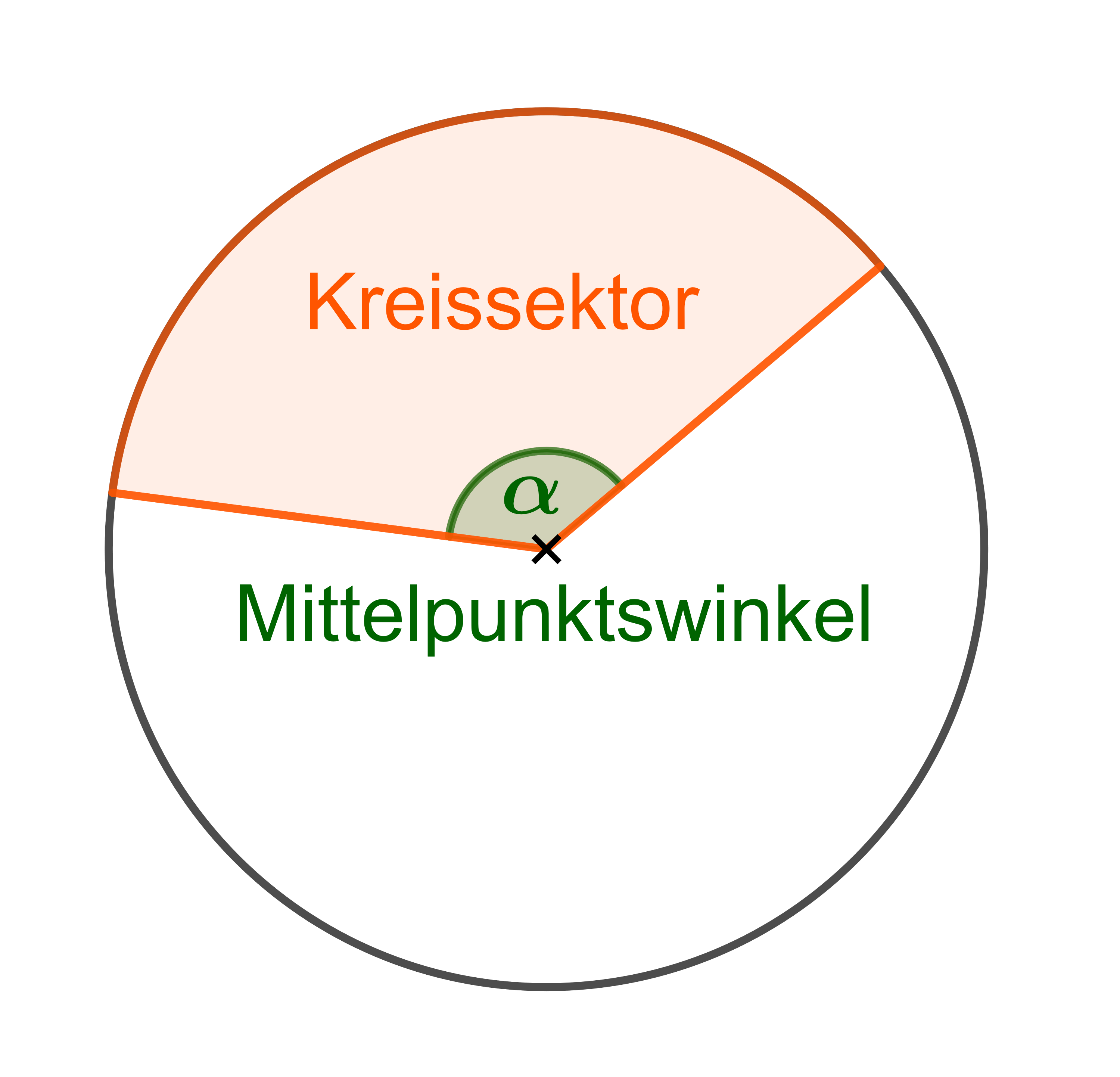
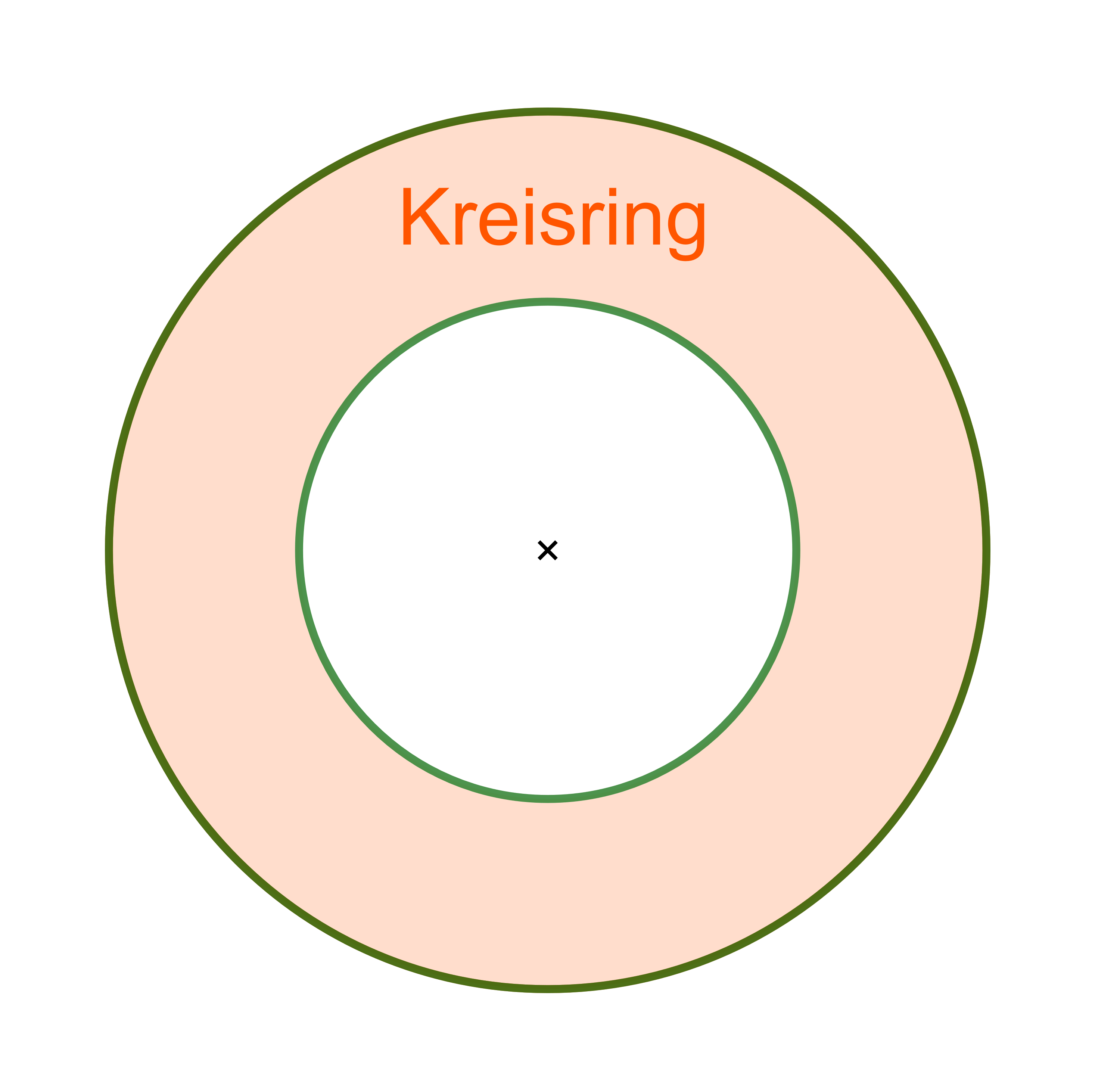
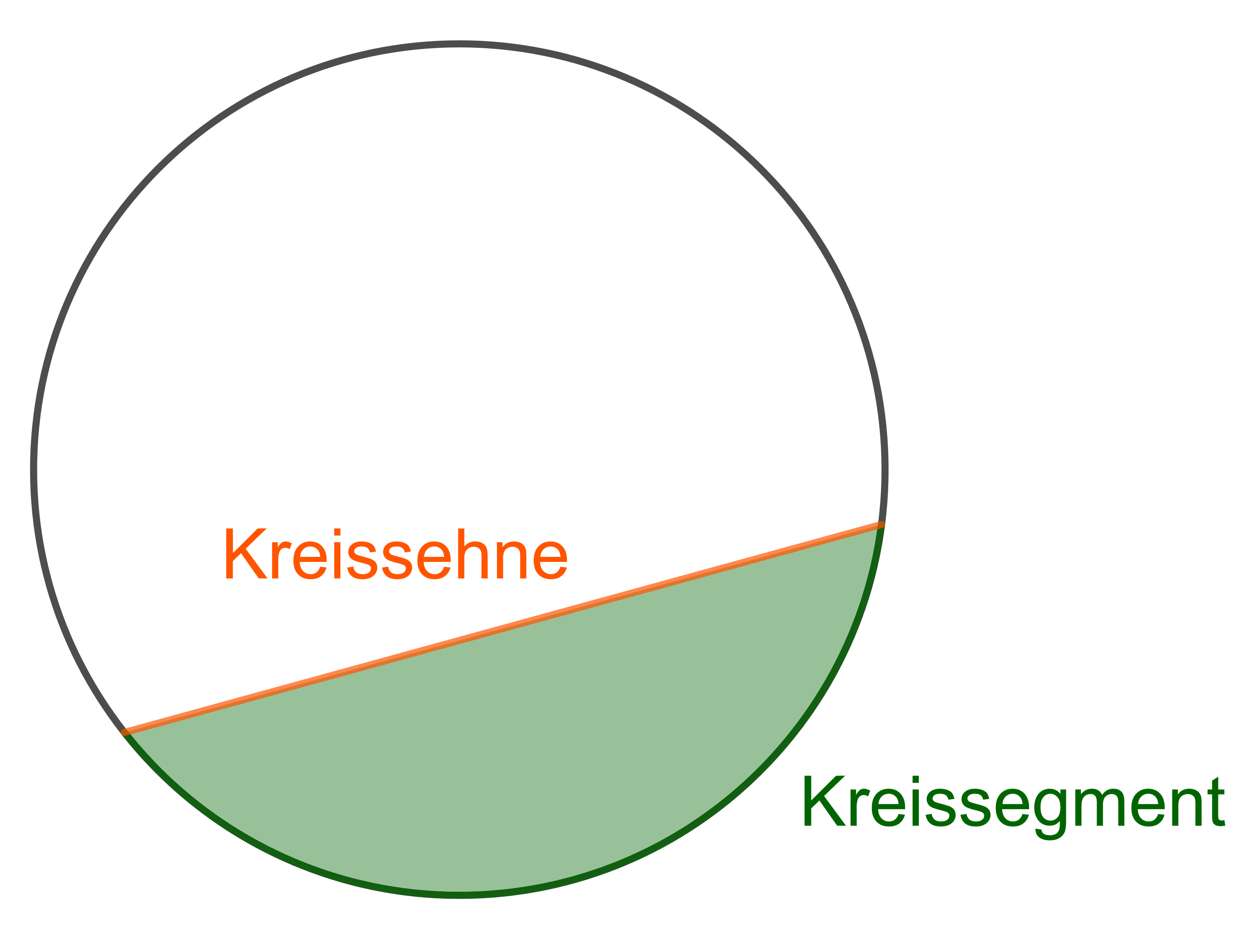
Weitere Begriffe - Kreisfläche, Kreissektor, Kreisumfang, Kreisring, Mittelpunktswinkel, Kreissehne, Kreissegment
Kreiszahl
Der Umfang und der Durchmesser eines Kreises stehen in einem besonderen Verhältnis. Dieses Verhältnis nennen wir :
Die Kreiszahl ist für jeden Kreis gleich und wird abgekürzt mit .
Mit der Kreiszahl kannst du den Umfang und die Fläche des Kreises berechnen.
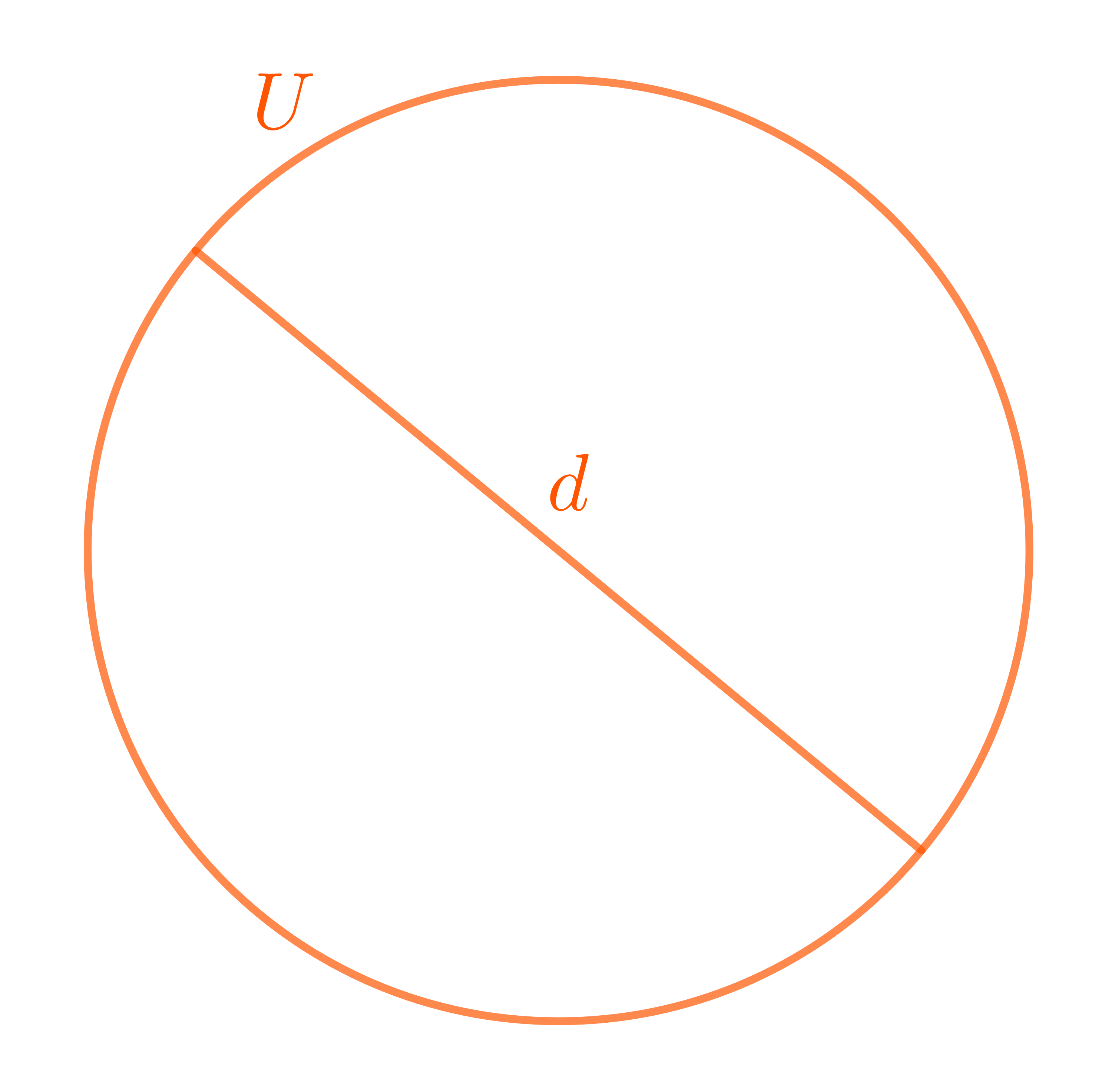
Übungsaufgaben
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Kreise und Kreisteile
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema: