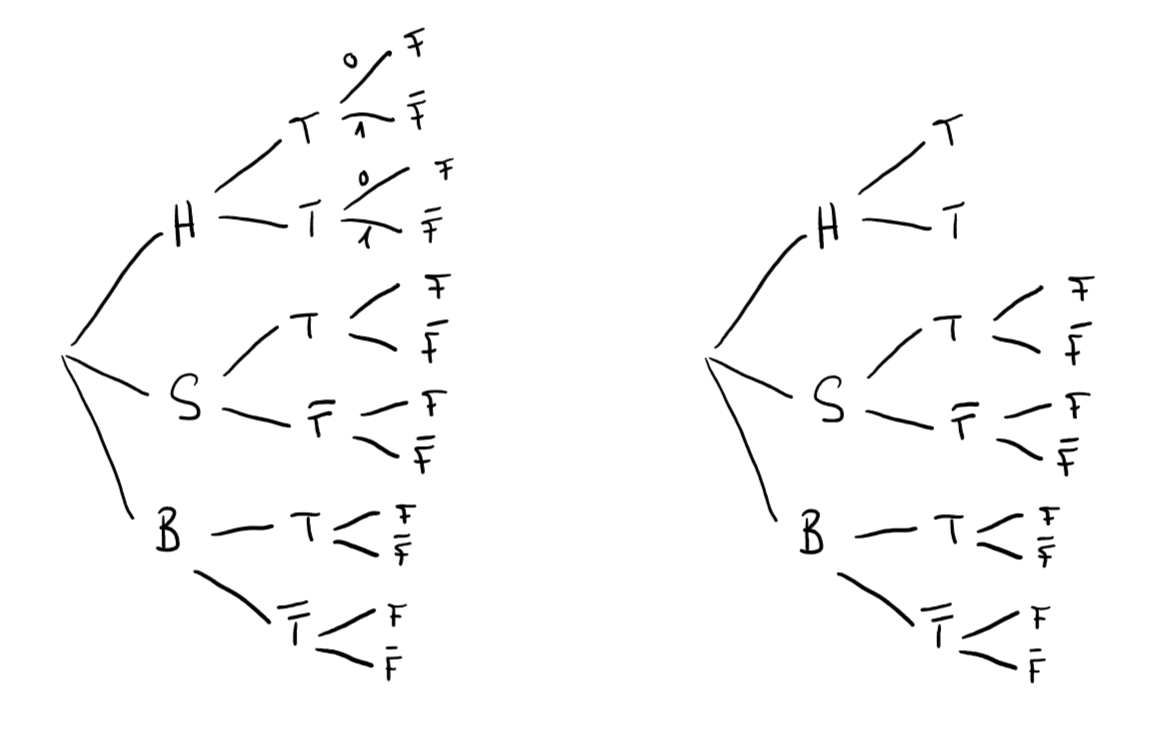
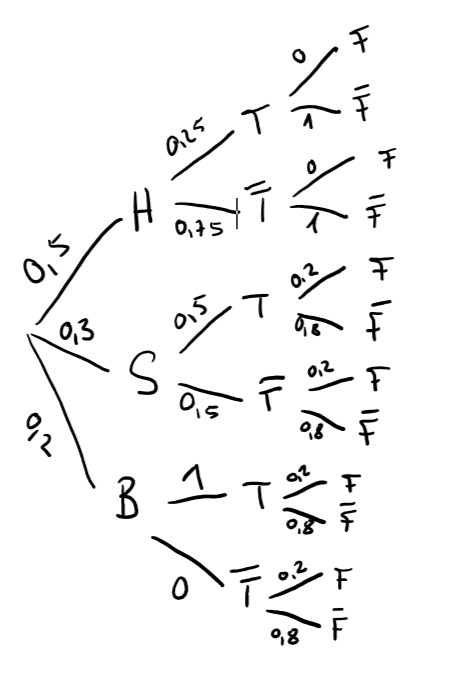
Ein großer Bergbauernhof bietet seinen Gästen während ihres Urlaubsaufenthalts verschiedene Möglichkeiten an, das Leben auf dem Land zu genießen. Erfahrungsgemäß entscheiden sich die Hälfte aller Gäste auf einer der einsamen Hütten (H) zur Ruhe zu kommen, 30% verbringen ihren Aufenthalt im gemütlichen Stadl (S) und die übrigen Besucher übernachten im Bauernhaus (B). Bei der Anreise hat jeder Gast die Wahl, den steilen Weg bis zum Feriendomizil zu Fuß zurückzulegen () oder sich von einem Traktorshuttle (T) nach oben befördern zu lassen. Von den Hüttenbewohnern nutzen nur ein Viertel diesen Service, bei den Stadlgästen sind es die Hälfte, und von den Gästen im Bauernhaus erklimmt keiner zu Fuß den Berg. Für Stadlgäste und Gäste des Bauernhauses besteht zusätzlich die Möglichkeit ein Frühstück (F) dazu zu buchen. Jeweils ein Fünftel der Gäste nutzen dieses Angebot nicht, unabhängig davon, ob der Shuttleservice in Anspruch genommen wird oder nicht. Hüttenbewohner können kein Frühstück buchen. Die Befragung eines zufällig ausgewählten Gastes nach seinen getätigten Buchungen wird als Zufallsexperiment aufgefasst.
Bestimmen Sie unter Verwendung eines Baumdiagramms die Wahrscheinlichkeiten aller Elementarereignisse des betrachteten Zufallsexperiments.
Gegeben sind folgende Ereignisse:
"Ein Gast entscheidet sich gegen den Aufstieg zum Bergbauernhof."
Geben Sie in aufzählender Mengenschreibweise an und berechnen Sie . Fassen Sie möglichst einfach in Worte und untersuchen Sie und auf Unvereinbarkeit.