Nachtermin Teil A - lernen mit Serlo!

🎓 Ui, schon Prüfungszeit? Hier geht's zur Mathe-Prüfungsvorbereitung.

Die freie Lernplattform

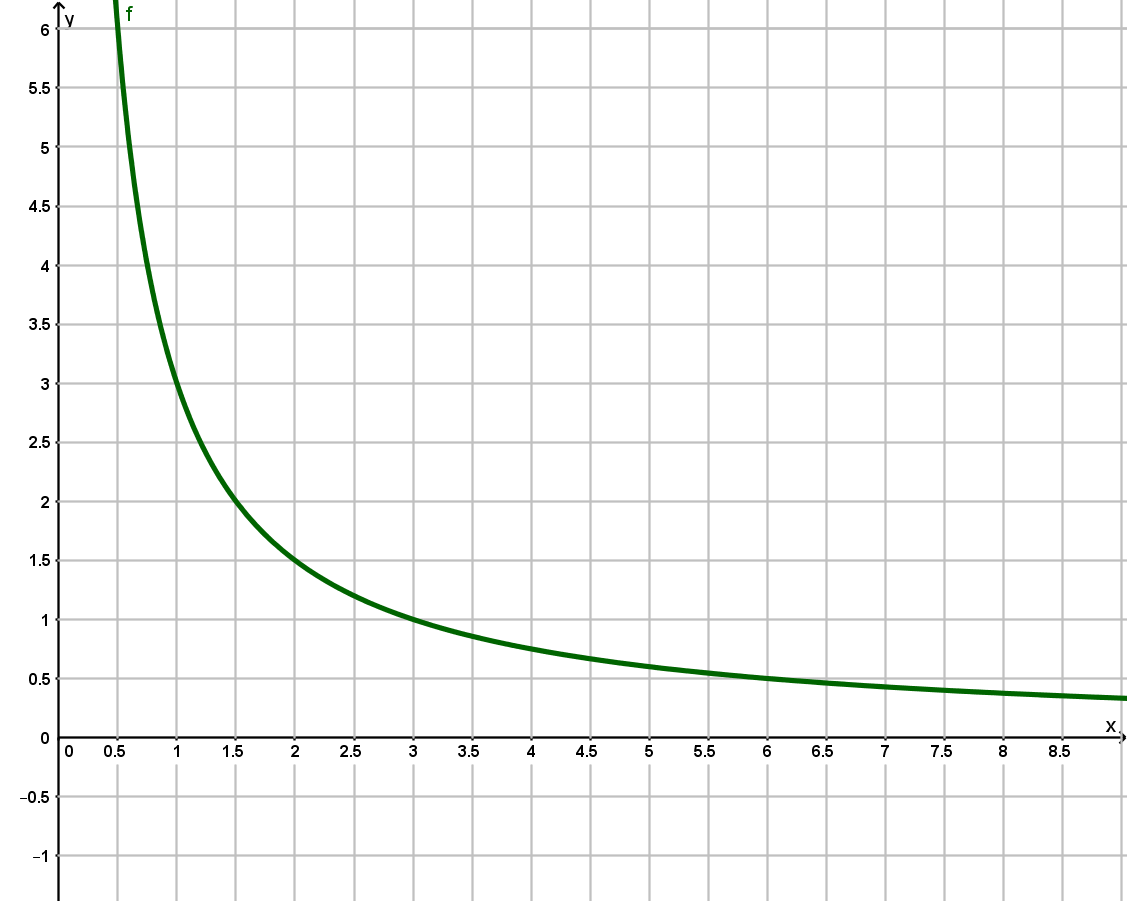
Gegeben ist die Funktion $f$ mit der Gleichung $y = \frac{3}{x}$ mit $𝔾 = ℝ^{+} \times ℝ^{+}$ .

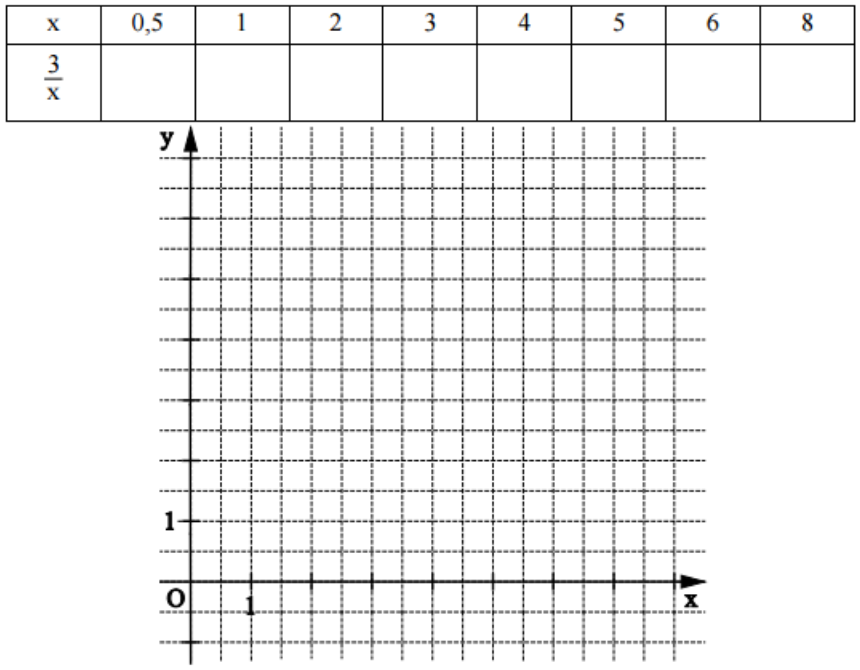
Ergänzen Sie die Wertetabelle auf zwei Stellen nach dem Komma gerundet.
Zeichnen Sie sodann den Graphen zu $f$ in das Koordinatensystem.

Lösung zur Teilaufgabe a
Du erhältst die Wertetabelle, wenn du die Werte in die Funktion $y = \frac{3}{x}$ einsetzt.
x
0,5
1
2
3
4
5
6
7
8
$\frac{3}{x}$
6
3
1,5
1
0,75
0,6
0,5
0,43
0,38
Zeichne diese Werte in ein Koordinatensystem
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
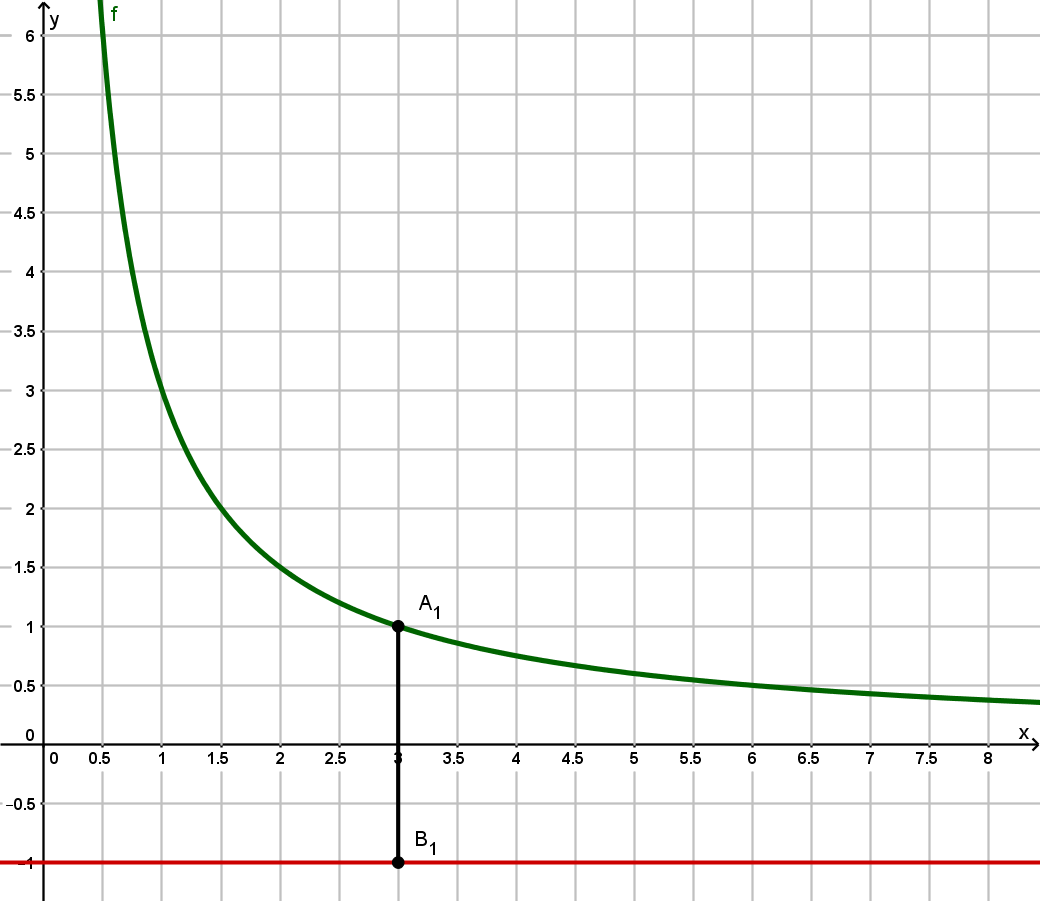
Punkte $A_{n} (x | \frac{3}{x})$ auf dem Graphen zu $f$ besitzen dieselbe Abszisse $x$ wie Punkte $B_{n}$ auf der Geraden $g$ mit der Gleichung $y = - 1$ mit $𝔾 = ℝ \times ℝ$ .
Für $x \in ℝ^{+}$ sind die Punkte $A_{n}$ und $B_{n}$ Endpunkte von Strecken $[A_{n} B_{n}]$ .
Zeichnen Sie die Gerade $g$ sowie die Strecke $[A_{1} B_{1}]$ für $x = 3$ in das Koordinatensystem zur Aufgabenstellung ein.

Lösung zur Teilaufgabe b
Da die Punkte $A_{n}$ auf der Funktion $f : y = \frac{3}{x}$ liegen und die Punkte $B_{n}$ auf der Gerade $g : y = - 1$ , gehst du beim x-Wert 3 auf den Funktionsgraphen von f, um $A_{1}$ zu erhalten und auf die Funktion g, für $B_{1}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Unter den Strecken $[A_{n} B_{n}]$ gibt es die Strecke $[A_{2} B_{2}]$ mit $A_{2} B_{2} = 6 LE$ .

Berechnen Sie den zugehörigen Wert für $x$ .

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das?

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.