Die Parabel verläuft durch die Punkte und . Sie hat eine Gleichung der Form mit und , .
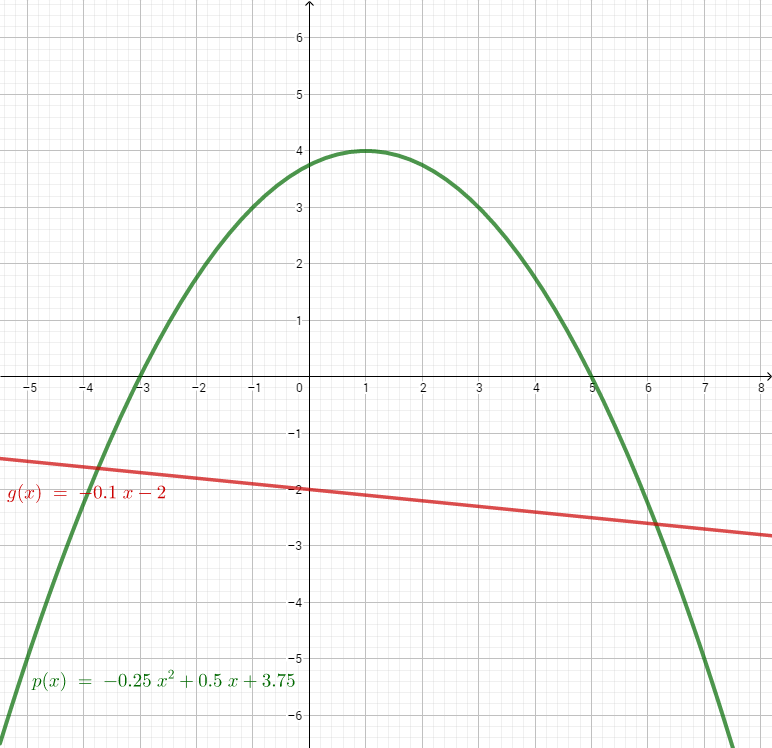
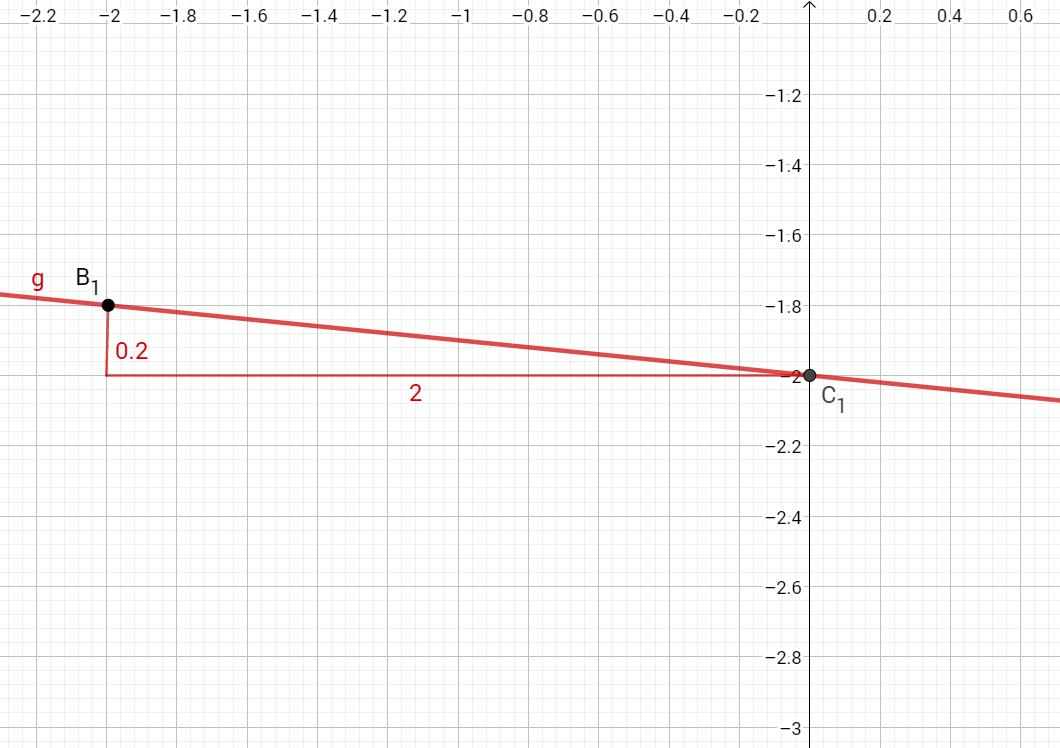
Die Gerade hat die Gleichung mit .
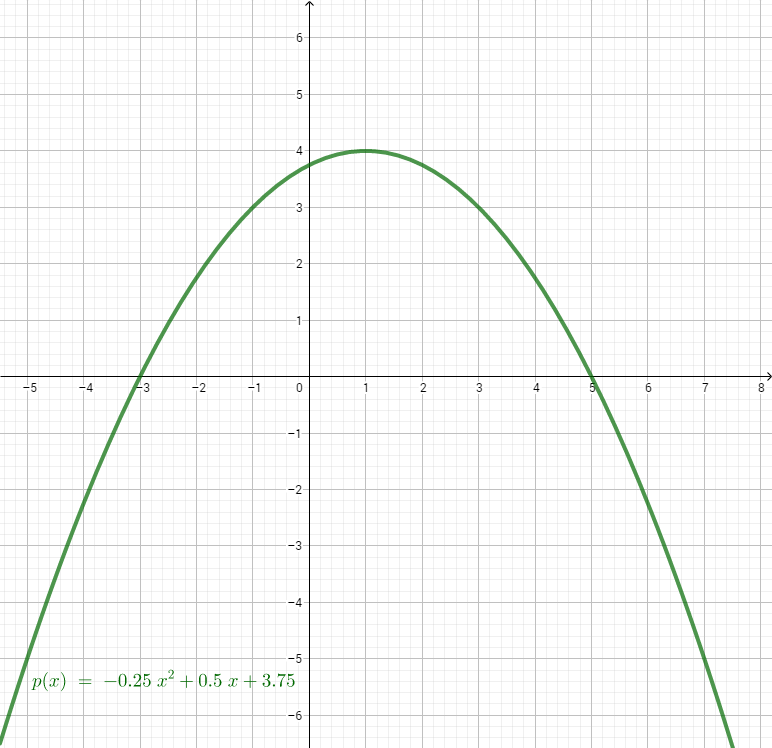
Zeigen Sie durch Berechnung der Werte für und , dass die Parabel die Gleichung hat.
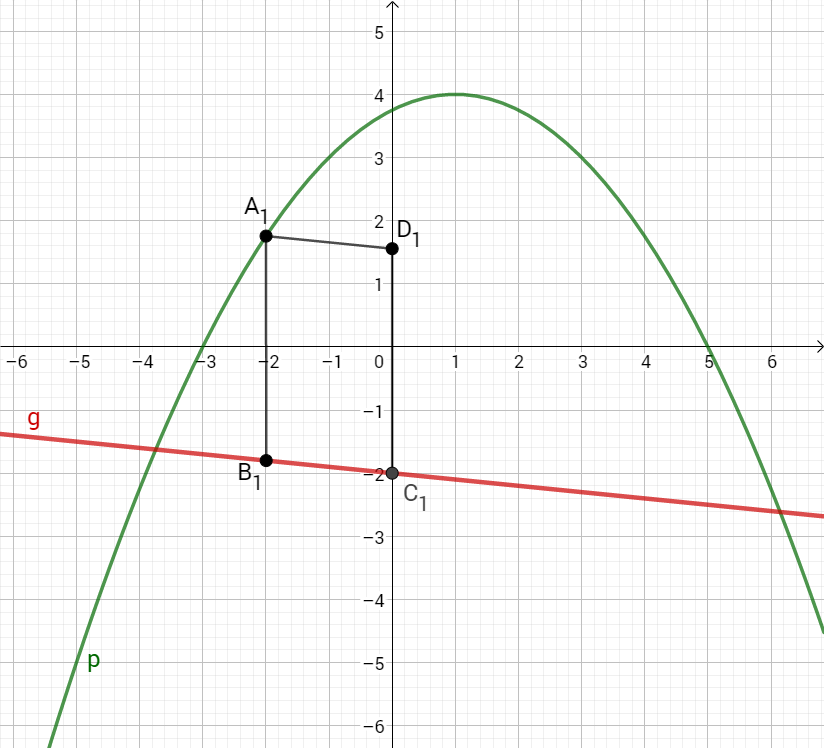
Zeichnen Sie sodann die Gerade sowie die Parabel für in ein Koordinatensystem ein.
Für die Zeichnung: Längeneinheit ;
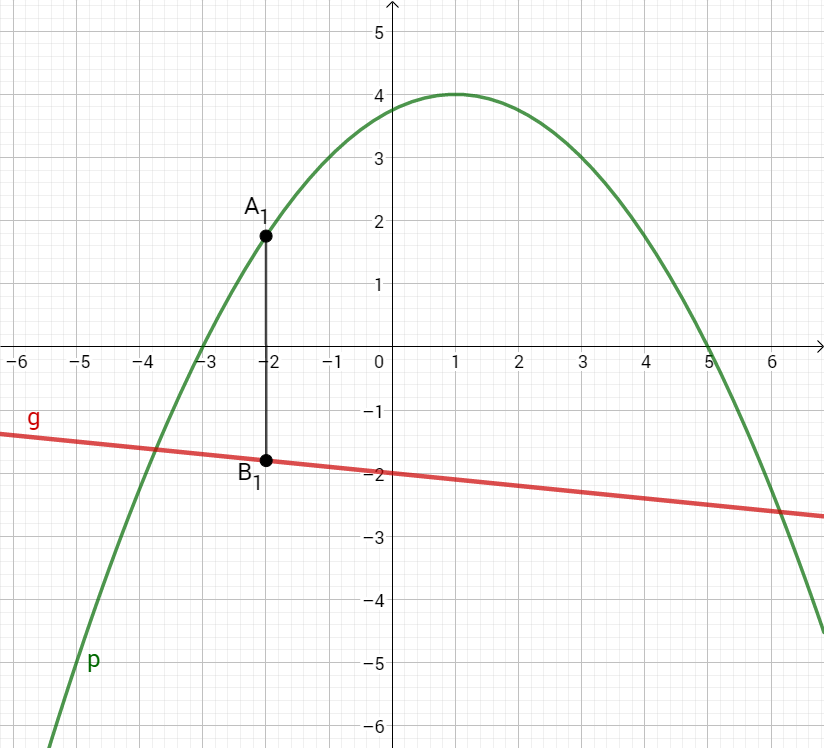
Punkte auf der Parabel und Punkte auf der Geraden haben dieselbe Abszisse .
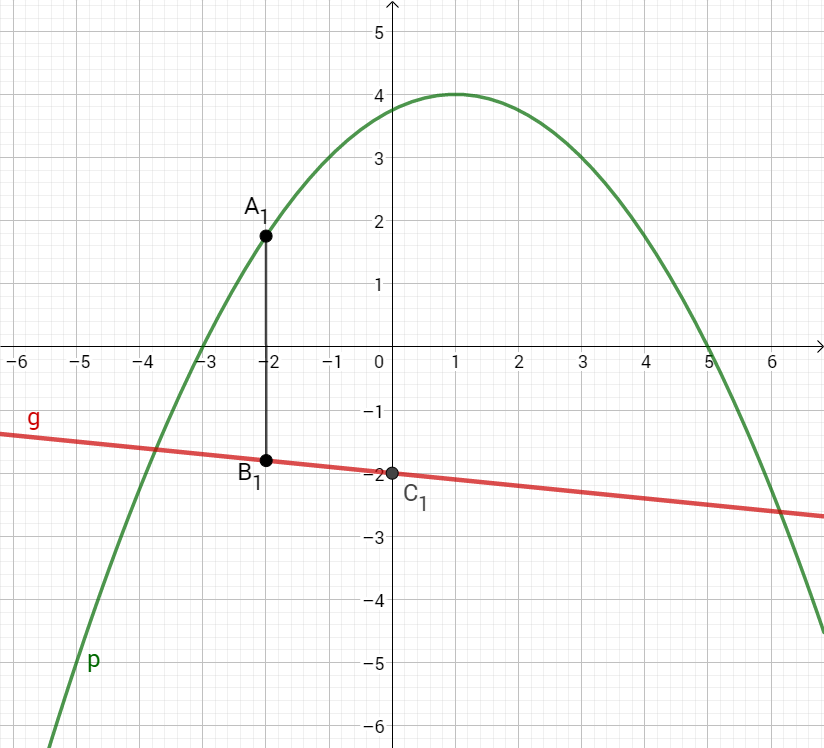
Sie sind zusammen mit Punkten und für die Eckpunkte von Parallelogrammen .
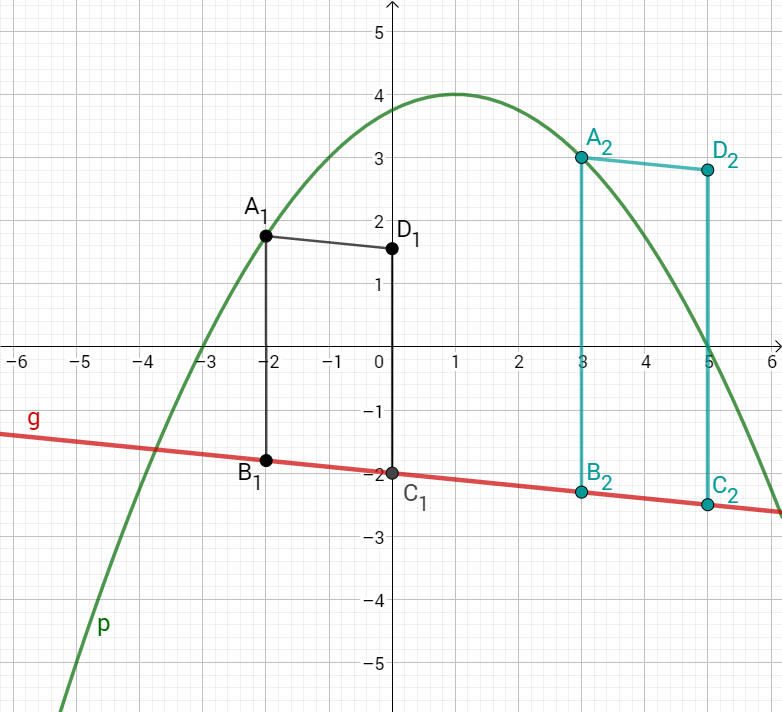
Die Punkte liegen ebenfalls auf der Geraden . Dabei ist die Abszisse der Punkte jeweils um größer als die Abszisse der Punkte .
Zeichnen Sie die Parallelogramme für und für in das Koordinatensystem zu Teilaufgabe b) ein.
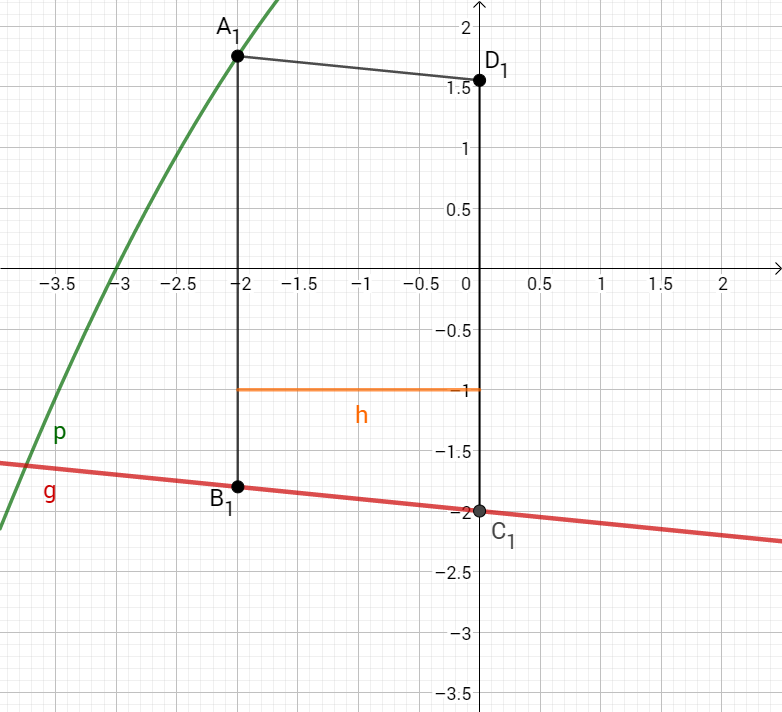
Berechnen Sie die Länge der Strecke in Abhängigkeit von der Abszisse der Punkte .
Ergebnis:
Überprüfen Sie rechnerisch, ob es unter den Parallelogrammen ein Parallelogramm mit dem Flächeninhalt von gibt.
Unter den Parallelogrammen gibt es die Rauten und . Berechnen Sie die -Koordinate der Punkte und auf zwei Stellen nach dem Komma gerundet. Teilergebnis:
Begründen Sie, dass es unter den Parallelogrammen kein Rechteck gibt.