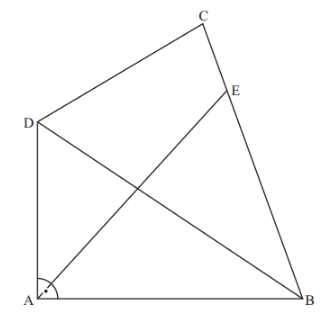
Die Zeichnung zeigt das Viereck .
Es gilt:
Runden Sie im Folgenden auf eine Stelle nach dem Komma.
Berechnen Sie die Länge der Diagonalen und den Flächeninhalt des Dreiecks .
Ergebnisse:
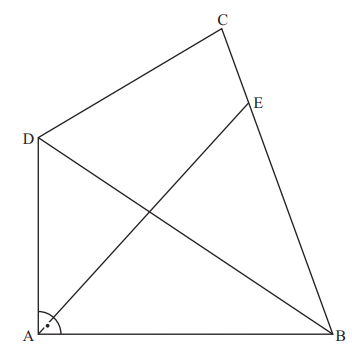
Der Punkt liegt auf der Strecke . Die Dreiecke und besitzen den gleichen Flächeninhalt. Berechnen Sie die Länge der Strecke .
Teilergebnis: ; Ergebnis:
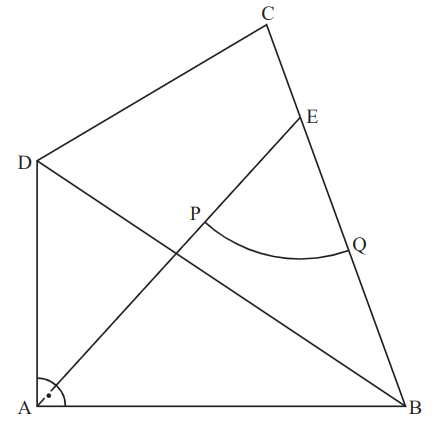
Der Kreis um mit dem Radius schneidet die Strecke im Punkt und die Strecke im Punkt .
Zeichnen Sie den Kreisbogen in die Zeichnung zur Aufgabenstellung ein. Berechnen Sie sodann den Flächeninhalt des Kreissektors, der durch die Strecken [], [] und den Kreisbogen begrenzt wird.