Teil A

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Die Anzahl der Ladestationen für Elektrofahrzeuge in Deutschland soll laut einer Prognose in den nächsten Jahren exponentiell wachsen. Diese Entwicklung kann man näherungsweise durch die Funktion $f:y=5000\cdot1{,}75^x\;\;\;$ $(\mathbb{G}=\mathbb{R}^+_0\times\mathbb{R}^+_0)$ beschreiben, wobei $x$ die Anzahl der Jahre und $y$ die Anzahl der Ladestationen darstellt.
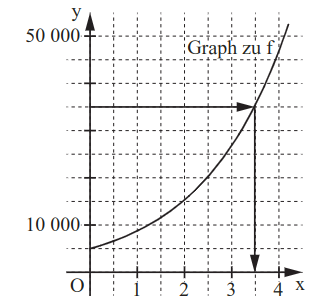
1. Ergänzen Sie die Wertetabelle auf Tausender gerundet und zeichnen Sie sodann den Graphen der Funktion $f$ in das Koordinatensystem ein.
  
  Für die Wertetabelle musst du wissen, wie man mit Potenzen rechnet.
  $\def\arraystretch{1.25} \begin{array}{l}5000\cdot1{,}75^0=5000\cdot1=5000\\5000\cdot1{,}75^1=5000\cdot1{,}75=8750\approx9000\\5000\cdot1{,}75^2=5000\cdot3{,}0625=15312{,}5\approx15000\\5000\cdot1{,}75^3=5000\cdot5{,}359375=26796{,}875\approx27000\\5000\cdot1{,}75^4=5000\cdot9{,}37890625=46894{,}53125\approx47000\end{array}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
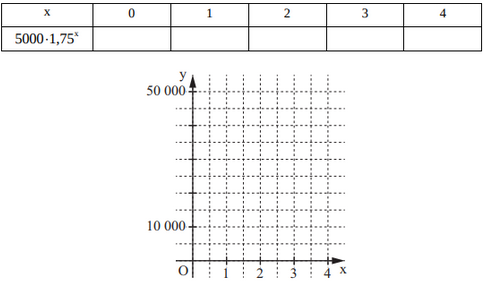
2. Ermitteln Sie mithilfe des Graphen, nach welcher Zeit die ursprüngliche Anzahl der Ladestationen erstmals um $600\;\%$ zugenommen haben wird.
  nach _ Jahren
  
  $5000$ Ladestationen entsprechen $100\;\%$ .
  $30000$ Ladestationen ergeben $600\;\%$ .
  Daraus ergibt sich eine Zunahme der Ladestationen um $30000$ von $5000$ auf $35000$ .
  Zeichne nun eine Parallele zur $x$ -Achse bei $35000$ ein.
  Durch den Schnittpunkt dieser Parallelen mit dem Graphen zeichne eine Parallele zur $y$ -Achse.
  Der Schnittpunkt dieser Parallelen mit der $x$ -Achse ergibt die gesuchte Anzahl von Jahren.
  Nach $3,5$ Jahren hat die ursprüngliche Anzahl der Ladestationen erstmals um $600\;\%$ zugenommen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Geben Sie an, welche jährliche Zunahme in Prozent in dieser Prognose angenommen wurde.
  %
  
  $f:\;y=5000\cdot1{,}75^x$
  Aus dem Faktor $1{,}75^x$ ergibt sich, dass in dieser Prognose ein jährliches Wachstum von $75 %$ angenommen wurde.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
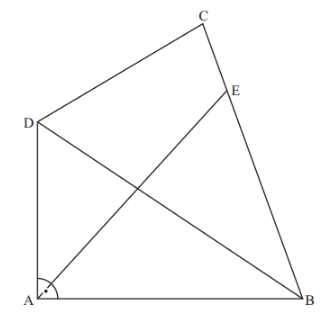
Die Zeichnung zeigt das Viereck $A B C D$ .
Es gilt:
$\def\arraystretch{1.25} \begin{array}{l}\overline{AB}=7{,}8\ \text{cm}\;\\\overline{AD}=5{,}2\ \text{cm}\\\overline{BC}=8{,}6\ \text{cm}\end{array}$
$\sphericalangle BAD=90^\circ,\;\sphericalangle CBA=70^\circ$
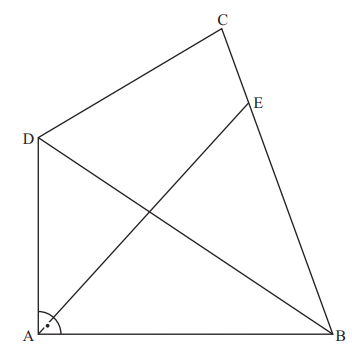
Runden Sie im Folgenden auf eine Stelle nach dem Komma.
1. Berechnen Sie die Länge der Diagonalen $[B D]$ und den Flächeninhalt $A$ des Dreiecks $B C D$ .
  $[$ Ergebnisse: $\overline{BD}=9{,}4\ \text{cm},\;A=23{,}9\ \text{cm}^2$ $]$
  
  Für die Berechnung der Länge der Diagonalen $[B D]$ benötigst Du den Satz des Pythagoras.
  $\overline{BD}^2=\overline{AB}^2+\overline{AD}^2=7{,}8\ \text{cm}^2+5{,}2\ \text{cm}^2=60{,}84\ \text{cm}^2$
  $\overline{BD}=\sqrt{87{,}88\ \text{cm}^2}=9{,}37\ \text{cm}$
  Auf eine Stelle nach dem Komma gerundet beträgt $\overline{BD}=9{,}4\ \text{cm}$ .
  Für die Berechnung der Dreiecksfläche $A_{ABC}$ musst Du wissen, wie man den Flächeninhalt eines Dreiecks berechnet.
  $A_{BCD}=\frac12\cdot a\cdot b\cdot\sin\left(\gamma\right)$
  $A_{BCD}=\frac12\cdot\overline{BD}\cdot\overline{BC}\cdot\sin\left(\gamma\right)$
  $A_{BCD}=\left(0{,}5\cdot9{,}4\cdot8{,}6\cdot\sin\left(\angle CBD\right)\right)\ \text{cm}^2$
  $\angle CBD=70^\circ-\angle DBA$
  Für die Berechnung des Winkels $\angle DBA$ berechne zunächst den Tangens des Winkels $\angle DBA$ , da $\overline{AD}$ und $\overline{AB}$ bekannt sind.
  $\tan\left(\angle DBA\right)=\dfrac{5{,}2}{7{,}8}=0{,}6666$
  $\def\arraystretch{1.25} \begin{array}{l}\angle DBA=33{,}7^\circ\\\angle CBD=70^\circ-33{,}7^\circ=36{,}3^\circ\end{array}$
  $A_{BCD}=(0{,}5\cdot9{,}4\cdot8{,}6\cdot\sin\left(36{,}3^\circ\right))\ \text{cm}^2$
  $A_{BCD}=(0{,}5\cdot9{,}4\cdot8{,}6\cdot0{,}5921)\ \text{cm}^2=23{,}9\ \text{cm}^2$
  Die Fläche $A_{BCD}$ des Dreiecks $B C D$ beträgt $23{,}9\ \text{cm}^2$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Der Punkt $E$ liegt auf der Strecke $[B C]$ . Die Dreiecke $A B E$ und $B C D$ besitzen den gleichen Flächeninhalt. Berechnen Sie die Länge der Strecke $[A E]$ .
  $[$ Teilergebnis: $\overline{BE}=6{,}5\ \text{cm}$ ; Ergebnis: $\overline{AE}=8{,}3\ \text{cm}$ $]$
  
  Die Dreiecke $A B E$ und $B C D$ besitzen den gleichen Flächeninhalt.
  $\displaystyle A_{BCD}=A_{ABE}$
  $\def\arraystretch{1.25} \begin{array}{l}23{,}9\ \text{cm}^2=0{,}5\cdot7{,}8\ \text{cm}\cdot\overline{BE}\cdot\sin\left(70^\circ\right)\\23{,}9\ \text{cm}^2=0{,}5\cdot7{,}8\ \text{cm}\cdot\overline{BE}\cdot0{,}93969\\\overline{BE}=6{,}5\ \text{cm}\end{array}$
  $\overline{AE}^2=\left(\overline{AB}^2+\overline{BE}^2-2\cdot\overline{AB}\cdot\overline{BE}\cdot\cos\left(70^\circ\right)\right)\ \text{cm}^2$
  $\overline{AE}^2=(7{,}8^2+6{,}5^2-2\cdot7{,}8\cdot6{,}5\cdot0{,}34)\ \text{cm}^2\hspace{1cm} |\sqrt{}$
  $\overline{AE}=8{,}3\ \text{cm}$
  Die Länge der Strecke $\overline{AE}$ beträgt $8{,}3\ \text{cm}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
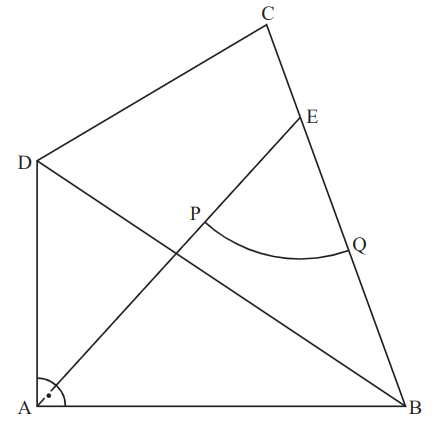
3. Der Kreis um $E$ mit dem Radius $3\ \text{cm}$ schneidet die Strecke $[A E]$ im Punkt $P$ und die Strecke $[B E]$ im Punkt $Q$ .
  Zeichnen Sie den Kreisbogen $\overset{\frown}{PQ}$ in die Zeichnung zur Aufgabenstellung ein. Berechnen Sie sodann den Flächeninhalt des Kreissektors, der durch die Strecken [ $Q E$ ], [ $E P$ ] und den Kreisbogen $\overset{\frown}{PQ}$ begrenzt wird.
  
  Für die Berechnung des Flächeninhaltes des Kreissektors, der durch die Strecken $[Q E]$ , $[E P]$ und den Kreisbogen $\overset{\frown}{PQ}$ begrenzt wird, musst du wissen, wie man die Fläche eines Kreissektors berechnet.
  $A_{Sektor}=r^2\cdot\mathrm\pi\cdot\dfrac{\angle\mathrm{PEQ}}{360°}\ \text{cm}^2$
  $A_{Sektor}=9\cdot\mathrm\pi\cdot\dfrac{\angle\mathrm{PEQ}}{360°}\ \text{cm}^2$
  Berechne den Winkel $\angle PEQ$
  $\angle AEB=\angle PEQ$
  Wende nun den Sinussatz im allgemeinen Dreieck an.
  $\dfrac{\sin\left(\angle AEB\right)}{7{,}8\ \text{cm}}$ $=\dfrac{\sin\left(70^\circ\right)}{8{,}3\ \text{cm}}$
  $\sin\left(\angle AEB\right)=\dfrac{0{,}94\cdot7{,}8\ \text{cm}}{8{,}3\ \text{cm}}$ $= 0,88$
  $\angle AEB=62{,}0^\circ$
  $\angle PEQ=62{,}0^\circ$
  $A_{Sektor}$ = $9\cdot\mathrm\pi\cdot\dfrac{62^\circ}{360^\circ}\ \text{cm}^2$ = $9\cdot3{,}14\cdot0{,}17\ \text{cm}^2$ = $4{,}9\ \text{cm}^2$
  Die Fläche des Kreissektors beträgt $4{,}9\ \text{cm}^2$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
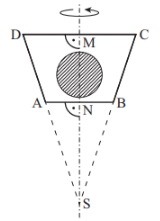
Die Skizze zeigt den Axialschnitt $A B C D$ eines Rotationskörpers mit der Rotationsachse $M S$ . Dieser Körper dient als Muster zur Herstellung einer Praline. Die Praline besteht aus Schokolade und einer kugelförmigen Cremefüllung. Der Anteil der Schokolade am Volumen der Praline beträgt $89 %$ . Es gilt: $\overline{MS}=5\ \text{cm}$ ; $\overline{MN}=2\ \text{cm}$ ; $\sphericalangle ADM=71{,}6^\circ.$
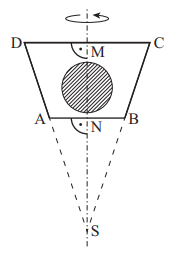
Runden Sie im Folgenden auf eine Stelle nach dem Komma.
1. Zeigen Sie rechnerisch, dass für die Strecken $[M D]$ und $[A N]$ gilt:
  $\overline{MD}=1{,}7\ \text{cm}$ und $\overline{AN}=1{,}0\ \text{cm}$ .
  
  Für diese Teilaufgabe musst du Kenntnisse über den Tangens im rechtwinkligen Dreieck haben.
  $\tan\left(\alpha\right)=\dfrac{\text{Gegenkathete}}{\text{Ankathete}}$
  Außerdem benötigst du den Strahlensatz.
  $\tan\left(\alpha\right)=\dfrac{\overline{MS}}{\overline{MD}}$
  $\tan\left(71{,}6^\circ\right)=\dfrac{5\ \text{cm}}{\overline{MD}}$
  $3{,}0=\dfrac{5\ \text{cm}}{\overline{MD}}$
  $\overline{MD}=1{,}7\ \text{cm}$
  Strahlensatz:
  $\dfrac{\overline{AN}}{1{,}7\ \text{cm}}=\dfrac{(5-2)\ \text{cm}}{5\ \text{cm}}$
  $\overline{AN}=\dfrac{3\ \text{cm}\cdot1{,}7\ \text{cm}}{5\ \text{cm}}=\dfrac{5{,}1\ \text{cm}^2}{5\ \text{cm}}=1{,}0\ \text{cm}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Errechnen Sie das Volumen $V$ der Cremefüllung.
  
  Für diese Aufgabe musst du wissen, wie man das Volumen eines Kegels berechnet.
  $V_{Kegel}=\dfrac13\cdot G\cdot h=\dfrac13\cdot r^2\cdot\mathrm\pi\cdot\mathrm h$
  $V_{Praline}=V_{Trapez \ ABCD}=V_{großer \ Kegel}-V_{kleiner \ Kegel}$
  $V_{Praline}=\left(\dfrac13\cdot1{,}7^2\cdot\mathrm\pi\cdot5 - \dfrac13 \cdot 1{,}0^2\cdot \pi \cdot (5-2)\right)\ \text{cm}^3$
  $V_{Praline}=\left(\dfrac13\cdot2{,}9\cdot3{,}14\cdot5-\frac13\cdot1{,}0^2\cdot3{,}14\cdot3\right)\ \text{cm}^3$
  $V_{Praline}=12{,}0\ \text{cm}^3$
  Der Anteil der Füllung an der Praline beträgt $(1 - 0,89) = 0,11$
  $V_{Füllung}=0{,}11\cdot12{,}0\ \text{cm}^3$
  $V_{Füllung}=1{,}3\ \text{cm}^3$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉