Aufgabe A1
Punkte liegen auf der Geraden mit der Gleichung .
Die Pfeile und mit spannen zusammen mit
Punkten für Parallelogramme auf.
In das Koordinatensystem sind die Gerade sowie das Parallelogramm für
eingezeichnet.
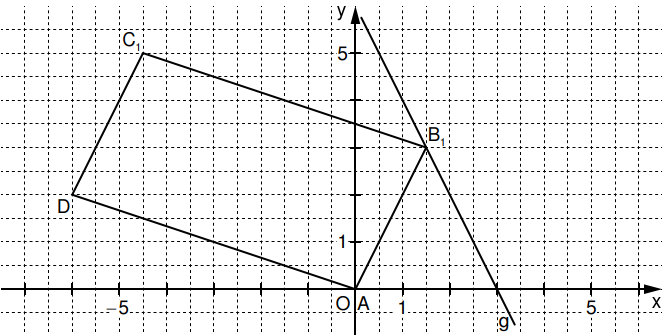
Überprüfen Sie rechnerisch, ob das Parallelogramm ein Rechteck ist. (2,5 P)
