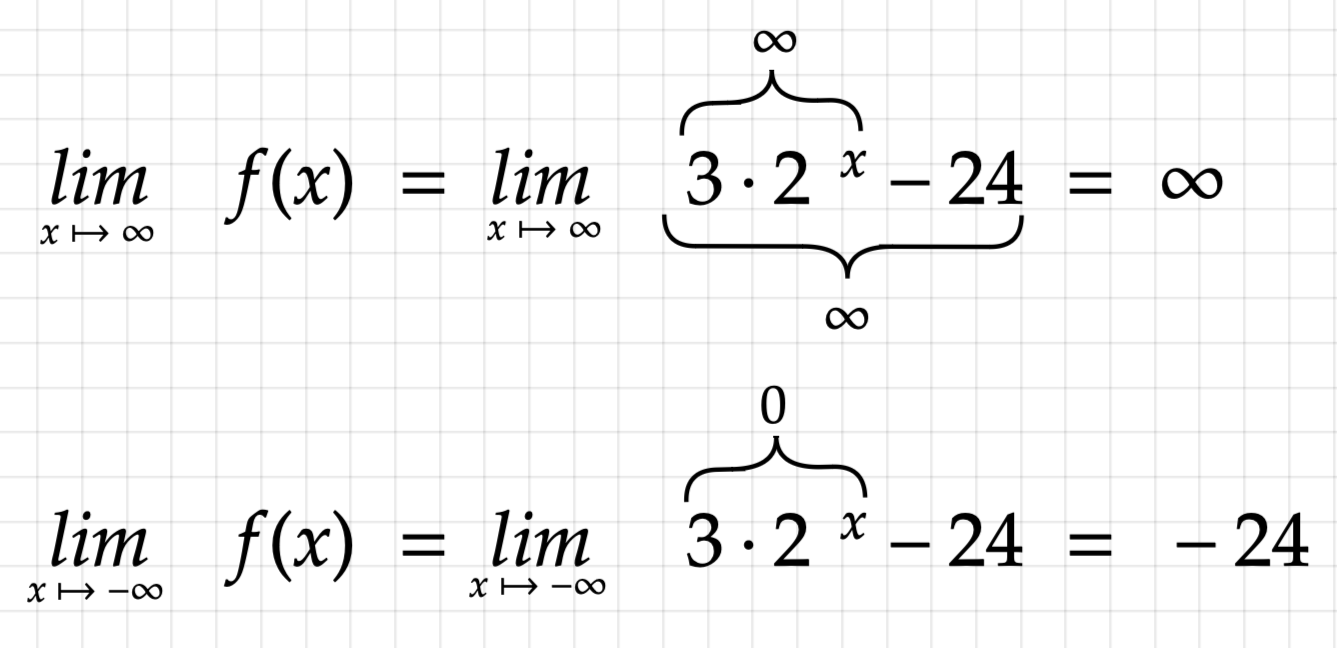Teil A

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

Nutze unser Training Realschule Bayern (Abschlussprüfung) und rechne dich fit für die Prüfung. Du findest dort einen Überblick über alle Themen und viele weitere Übungsmöglichkeiten.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe A1
Punkte $B_{n}$ liegen auf der Geraden $g$ mit der Gleichung $y = - 2 x + 6$ $(x, y \in ℝ)$ .
Die Pfeile $\vec{A B_{n}} (x) = (\begin{array}{c} x \\ - 2 x + 6 \end{array})$ und $\vec{A D} = (\begin{array}{c} - 6 \\ 2 \end{array})$ mit $A (0 | 0)$ spannen zusammen mit
Punkten $C_{n}$ für $x < 3,6$ Parallelogramme $A B_{n} C_{n} D$ auf.
In das Koordinatensystem sind die Gerade $g$ sowie das Parallelogramm $A B_{1} C_{1} D$ für
$x = 1,5$ eingezeichnet.
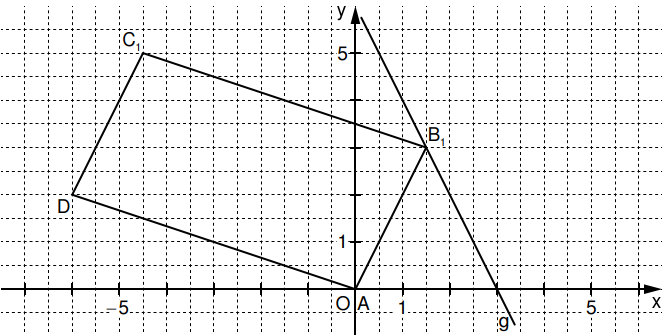
1. Überprüfen Sie rechnerisch, ob das Parallelogramm $A B_{1} C_{1} D$ ein Rechteck ist. (2,5 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt von Vektoren
  Zunächst sammeln wir unser Wissen und setzen es in den Kontext
  Damit es sich bei dem Parallelogramm $A B_{n} C_{n} D$ um ein Rechteck handelt, müssen alle Seiten senkrecht aufeinander stehen.
  Ist das Skalarprodukt zweier Vektoren $= 0$ , stehen die beiden senkrecht aufeinander.
  Nun berechnen wir die relevanten Vektoren
  $\vec{A B_{1}}$ : Setze $x = 1,5$ in den allgemeinen Vektor $\vec{A B_{n}}$
  $\vec{A B_{1}} = (\begin{array}{c} 1,5 \\ - 2 \cdot 1,5 + 6 \end{array}) = (\begin{array}{c} 1,5 \\ 3 \end{array})$
  $\vec{A D} = (\begin{array}{c} - 6 \\ 2 \end{array})$
  Im nächsten Schritt Berechnen wir das Skalarprodukt aus diesen beiden Vektoren
  $(\begin{array}{c} 1,5 \\ 3 \end{array}) \circ (\begin{array}{c} - 6 \\ 2 \end{array}) = 1,5 \cdot (- 6) + 3 \cdot 2 = - 9 + 6 = - 3$
  Wir treffen eine Entscheidung
  Für das Skalarprodukt gilt: $\vec{A B_{1}} \circ \vec{A D} = - 3 \neq 0$ ,
  damit stehen die Vektoren nicht senktrecht aufeinander.
  Das Parallelogramm $A B_{n} C_{n} D$ ist also kein Rechteck.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne zunächst den Vektor $\vec{A B_{1}}$
  Überprüfe, ob $\vec{A B_{1}}$ und $\vec{A D}$ senkrecht aufeinander stehen, indem du das Skalarprodukt berechnest.
  Triff nun eine Entscheidung: Was bedeutet es geometrisch, wenn die beiden Vektoren nicht senkrecht aufeinander stehen?
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe A2
Gegeben ist die Funktion $f$ mit der Gleichung $y = 3 \cdot 2^{x} - 24$ $(x, y \in ℝ)$ .
1. Berechnen Sie die Nullstelle der Funktion $f$ . (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialgleichung
  Funktion 0 setzen und Gleichung auflösen
  $f (x)$ $=$ $0$
  $0$ $=$ $3 \cdot 2^{x} - 24$
  Wir lösen so weit wie möglich nach $x$ auf:
  $0$ $=$ $3 \cdot 2^{x} - 24$ $+ 24$
  $24$ $=$ $3 \cdot 2^{x}$ $: 3$
  $8$ $=$ $2^{x}$
  Untersuche, wie oft die 2 mit sich selbst multipliziert werden muss
  $x = 3$ , weil $2^{3} = 2 \cdot 2 \cdot 2 = 8$ ist.
  $\begin{array}{l} \Rightarrow 𝕃 = {3} \end{array}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Setze die Gleichung $= 0$
  Löse die Gleichung so weit wie möglich auf.
  Die Schwierigkeit liegt darin, dass x im Exponenten steht: Untersuche mit der Gleichung, wie oft die 2 mit sich selbst multipliziert werden muss, um den Wert der anderen Seite zu entsprechen.
2. Geben Sie die Gleichung der Asymptote des Graphen von $f$ an. (1 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Asymptoten von Exponentialfunktionen
  Grenzwertverhalten der Funktion f
  Die Funktion hat also eine waagrecht Asymptote bei $y = - 24$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Für die Bearbeitung kannst du zwischen verschiedenen Lösungswegen wählen:
  Skizziere den Graphen und bestimme so die Asymptote.
  Führe eine Grenzwertbetrachtung durch.
  Lies die Asymptote von der Funktionsgleichung ab.
3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe A3
Ein Glücksrad besteht aus drei kongruenten Sektoren, die wie abgebildet
beschriftet sind.
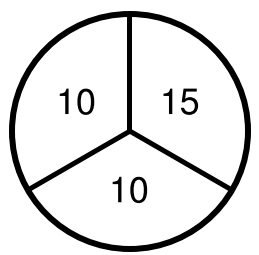
1. Lionel dreht dreimal am Glücksrad.
  Geben Sie die Wahrscheinlichkeit dafür an, dass er dreimal die Zahl $10$ erhält. (1 P)
  %
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
  Einzelwahrscheinlichkeiten
  Von 3 Teilen, steht auf 1 Teil die Zahl 15, also: $P (15) = \frac{1}{3}$
  Von 3 Teilen, steht auf 2 Teilen die Zahl 10, also: $P (10) = \frac{2}{3}$
  Gesuchte Wahrscheinlichkeit
  Dafür stellen wir uns ein Baumdiagramm vor, bei dem wir dreimal den Pfad mit der Zahl 10 Entlanggehen.
  Die Wahrscheinlichkeit, eine 10 zu drehen, beträgt $\frac{2}{3}$
  Die Gesamtwahrscheinlichkeit berechnen wir mit der Pfadregel:
  $P (10,10,10) = \frac{2}{3} \cdot \frac{2}{3} \cdot \frac{2}{3} = \frac{8}{27} = 0,2963 \approx 29,63 %$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne zuerst die Wahrscheinlichkeit dafür, eine $10$ zu ziehen: $P (10)$
  Berechne anschließend die Wahrscheinlichkeit $P (10,10,10)$ mithilfe der Pfadregel.
2. Christiane dreht nur zweimal am Glücksrad.
  Bestimmen Sie die Wahrscheinlichkeit dafür, dass sie zweimal hintereinander die
  gleiche Zahl erhält. (2 P)
  %
  
  Kombinationen, bei denen zweimal die gleiche Zahl gedreht wird
  Christiane zieht $2$ mal die $10$ mit $P (10,10) = \frac{2}{3} \cdot \frac{2}{3}$
  Sie zieht $2$ mal die $15$ mit $P (15,15) = \frac{1}{3} \cdot \frac{1}{3}$
  Gesamtwahrscheinlichkeit
  $P (gesamt) = P (10,10) + P (15,15)$
  $= \frac{2}{3} \cdot \frac{2}{3} + \frac{1}{3} \cdot \frac{1}{3} = \frac{5}{9} = 0,5555... \approx 55,56 %$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Überlege dir, welche Kombinationen die Bedienung erfüllen. Hier könnte ein Baumdiagramm helfen.
  Berechne für diese Kombinationen die Wahrscheinlichkeiten. Nutze hierfür die Pfadregel.
  Berechne die Gesamtwahrscheinlichkeit, indem du die Wahrscheinlichkeiten der einzelnen Kombinationen addierst.
4
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe A4
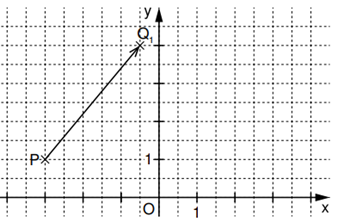
Der Punkt $P (- 3 | 1)$ legt zusammen mit Punkten $Q_{n}$ für $φ \in [0^{\circ}; 180^{\circ}]$ Pfeile
$\vec{P Q_{n}} (φ) = (\begin{array}{c} 2,5 + \sin φ \\ 3 \end{array})$ fest.
1. Zeichnen Sie den Pfeil $\vec{P Q_{1}}$ für $φ = 0^{\circ}$ in das Koordinatensystem ein. (1 P)
  
  Wir berechnen zunächst den Vektor $\vec{P Q_{1}}$
  Dafür setzen wir $φ = 0^{\circ}$ in $\vec{P Q_{n}}$ ein:
  $\vec{P Q_{1}} (0) = (\begin{array}{c} 2,5 + \sin (0) \\ 3 \end{array}) = (\begin{array}{c} 2,5 \\ 3 \end{array})$
  Nun berechnen wir die Koordinaten des Punktes $Q_{1}$
  Der Vektor $\vec{P Q_{1}}$ ergibt sich aus den Koordinaten des Fußpunktes $P (- 3 | 1)$ und den Koordinaten der Spitze $Q_{1} (q_{x_{1}} | q_{y_{1}})$ .
  Nach dem Prinzip "Spitze minus Fuß" gilt:
  $(\begin{array}{c} 2,5 \\ 3 \end{array}) = \underset{Spitze - Fuß}{\underset{⏟}{(\begin{array}{c} q_{1 x} - (- 3) \\ q_{1 y} - 1 \end{array})}}$
  Wenn man den Vektor zeilenweise ließt, ergeben sich folgende Terme:
  $\begin{array}{l} (1) 2,5 = q_{1 x} - (- 3) ⟹ q_{1 x} = 2,5 - 3 = - 0,5 \\ (2) 3 = q_{1 y} - 1 ⟹ q_{1 y} = 3 + 1 = 4 \\ ⟹ Q_{1} (- 0,5 | 4) \end{array}$
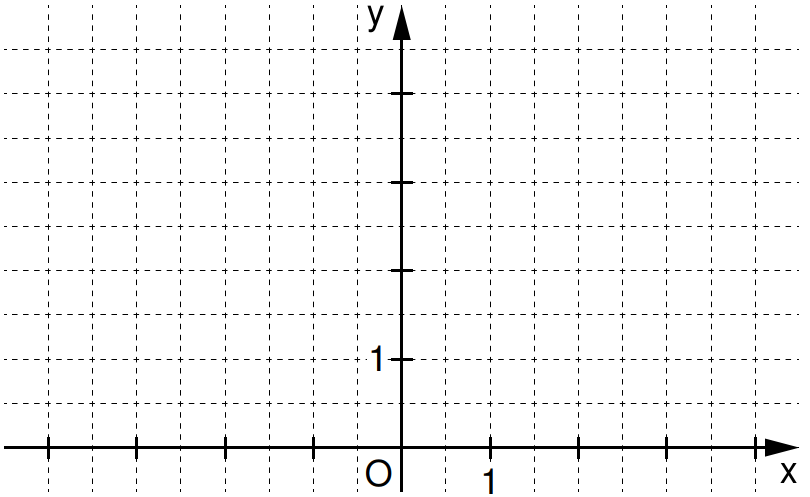
  Nun kennen wir beide Punkte und müssen diese nur noch in das Koordinatensystem einzeichnen.
  Darstellung im Koordinatensystem
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Setze $φ = 0^{\circ}$ in den Pfeil ein. So erhältst du $\vec{P Q_{1}}$ .
  Berechne nun die Koordinaten des Punktes $Q_{1}$ , indem du dir überlegst, wie sich der Vektor $\vec{P Q_{1}}$ zusammensetzt. (Tipp: Nutze die Regel "Spitze minus Fuß").
  Übertrage die Koordinaten in dein Koordinatensystem.
2. Für den Pfeil $\vec{P Q_{2}}$ gilt: $\vec{P Q_{2}} = (\begin{array}{c} 3 \\ 3 \end{array})$ .
  Bestimmen Sie die zugehörigen Werte von $φ$ . (2 P)
  
  Wir setzen $\vec{P Q_{2}}$ mit unserem Pfeil gleich:
  $(\begin{array}{c} 3 \\ 3 \end{array})$ $=$ $(\begin{array}{c} 2,5 + \sin φ \\ 3 \end{array})$
  Für die Berechnung von $φ$ ist nur die erste Zeile relevant.
  Wir lösen die erste Zeile nach $φ$ auf:
  $3$ $=$ $2,5 + \sin φ$ $- 2,5$
  $0,5$ $=$ $\sin φ$ $\sin^{- 1} ()$
  $φ$ $=$ $30 ° oder 150 °$
  $𝕃 = {30 °; 150 °}$
  
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne den Winkel $(φ)$ aus der x-Koordinate von Vektor $\vec{P Q_{n}} (φ)$ mit y-Koordinate von $\vec{P Q_{2}}$ .

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$0$	$=$	$3 \cdot 2^{x} - 24$	$+ 24$
$24$	$=$	$3 \cdot 2^{x}$	$: 3$
$8$	$=$	$2^{x}$

$3$	$=$	$2,5 + \sin φ$	$- 2,5$
$0,5$	$=$	$\sin φ$	$\sin^{- 1} ()$
$φ$	$=$	$30 ° oder 150 °$

Teil A

Aufgabe A1

Zunächst sammeln wir unser Wissen und setzen es in den Kontext

Nun berechnen wir die relevanten Vektoren

Im nächsten Schritt Berechnen wir das Skalarprodukt aus diesen beiden Vektoren

Wir treffen eine Entscheidung

Hast du eine Frage oder Feedback?

Aufgabe A2

Funktion 0 setzen und Gleichung auflösen

Untersuche, wie oft die 2 mit sich selbst multipliziert werden muss

Hast du eine Frage oder Feedback?

Grenzwertverhalten der Funktion f

Hast du eine Frage oder Feedback?

Aufgabe A3

Einzelwahrscheinlichkeiten

Gesuchte Wahrscheinlichkeit

Hast du eine Frage oder Feedback?

Kombinationen, bei denen zweimal die gleiche Zahl gedreht wird

Gesamtwahrscheinlichkeit

Hast du eine Frage oder Feedback?

Aufgabe A4

Wir berechnen zunächst den Vektor PQ1→

Nun berechnen wir die Koordinaten des Punktes Q1

Nun kennen wir beide Punkte und müssen diese nur noch in das Koordinatensystem einzeichnen.

Hast du eine Frage oder Feedback?

Wir setzen PQ2→ mit unserem Pfeil gleich:

Wir lösen die erste Zeile nach φ auf:

Hast du eine Frage oder Feedback?

Wir berechnen zunächst den Vektor $\vec{P Q_{1}}$

Nun berechnen wir die Koordinaten des Punktes $Q_{1}$

Wir setzen $\vec{P Q_{2}}$ mit unserem Pfeil gleich:

Wir lösen die erste Zeile nach $φ$ auf: