Stellenwertsysteme sind Zahlensysteme, die nach dem Bündelungsprinzip funktionieren. Jeder Stelle einer Zahl wird dabei ein Wert zugeordnet. Die bekanntesten Stellenwertsysteme sind das Dezimalsystem und das Binärsystem.
Geschichte
Bevor es Zahlen gab, notierte man Anzahlen durch verschiedene Symbole, wie z.B. Striche oder Punkte. Um zu schreiben, dass man 5 Schafe sieht, notierte man also 5 Striche: ||||| oder auch Punkte: .

Quelle: Wikimedia Commons
Je größer die Zahlen werden, umso unübersichtlicher wird dieses System. Außerdem hat es noch andere Grenzen. Es ist z.B. nicht möglich oder sehr umständlich, negative Zahlen oder Anteile (=Brüche) darzustellen.
Mithilfe von Stellenwertsystemen ist es einfacher, Zahlen darzustellen und komplizierte Rechnungen durchzuführen.
Verschiedene Stellenwertsysteme
Es gibt ausführliche Artikel zu folgenden Stellenwertsystemen:
Dezimalsystem
Das Dezimalsystem stellt Zahlen zur Basis 10 dar und ist unser alltägliches Zahlsystem.
Binärsystem und Hexadezimalsystem
Binär- und Hexadezimalsystem stellen Zahlen zur Basis 2 bzw. 16 dar. Sie werden heute in der Datentechnik bzw. Datenverarbeitung genutzt.
Grundlagen
Stellenwertsysteme liefern zwei Informationen auf einen Blick, denn die Ziffer selbst und die Stelle, an der sie steht, verraten etwas:
Die Stelle, an der die Ziffer steht, verrät die Bündelungseinheit,
die Ziffer verrät die Anzahl der Bündel.
Man will die Anzahl der blauen Punkte in einer Zahl ausdrücken.
1. Ordnen!
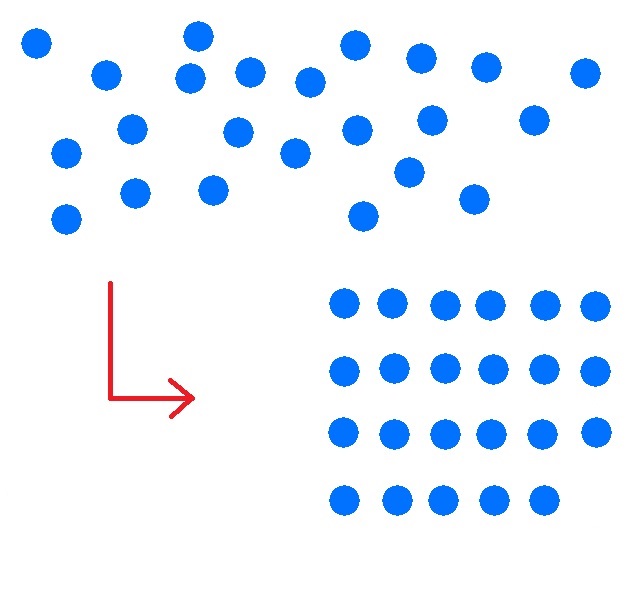
2.Bündeln!
Fasse immer 5 Punkte zu einem Bündel zusammen.
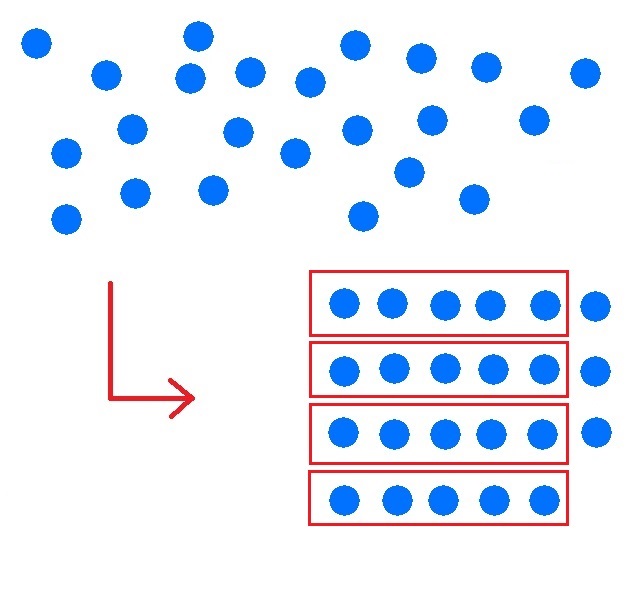
3. Zählen!
Man zählt 4 Bündel und 3 einzelne Punkte.
Die Anzahl der Bündel schreibt man zuerst auf und dann die Anzahl der einzelnen Punkte.

Weil immer 5 Punkte zusammengefasst wurden, kommt "43" als Anzahl heraus, obwohl es 23 Punkte sind. Um die bekannte 23 zu erhalten, muss man immer zehn Punkte zu einem Bündel fassen.
Die Null
Um alle Anzahlen auf diese Weise beschreiben zu können, musste man sich einen "Platzhalter" überlegen, der z.B. sagt, dass es keine einzelnen Punkte gibt, sondern nur Bündel. Dieser Platzhalter war die Null.
"Vier Zehner-Bündel und kein einzelner Punkt" konnte man jetzt, da die Null erfunden war, kurz schreiben als . Denn jeder weiß, wenn die 4 an der zweiten Stelle von rechts steht, beschreibt sie Zehner.
Begriffe und Notation
Basis: Die Basis beschreibt die Anzahl der Punkte, die zu einem Bündel zusammengefasst werden. Im Beispiel rechts wäre die Basis also 6.
Ziffern: Wenn die Basis eines Systems ist, gibt es in diesem System genau Ziffern. Im Beispiel rechts gibt es also die 6 Ziffern 0, 1, 2, 3, 4 und 5.
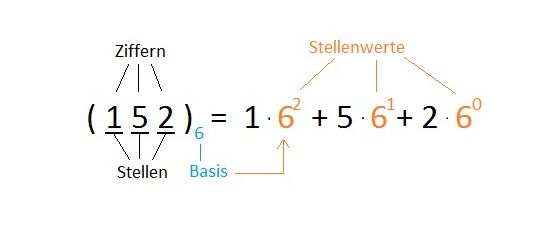
Stelle und Stellenwert: Der Platz einer Ziffer heißt Stelle. Jeder Stelle wird ein Stellenwert zugeordnet. Dieser Stellenwert beträgt , wobei man Stellen von rechts nach links mit 0 beginnend nummeriert. Die ersten drei Stellenwerte zur Basis sechs sind also und .
Um deutlich zu machen, in welchem Stellenwertsystem man eine Zahl ausdrückt, benutzt man einen Index, der die Basis angibt:
Die Basis 10 bedeutet, dass man sich im Dezimalsystem befindet.
Stellenwerttafel
In einer Stellenwerttafel stehen in der ersten Zeile die Stellenwerte, sodass darunter die Ziffern der Zahl geschrieben werden können.
Die Zahl hätte also diese Stellenwerttafel.
Stellenwert | ||||||
|---|---|---|---|---|---|---|
1 | 0 | 3 | 2 |
Im Dezimalsystem schreibt man auch E, Z, H,… für Einer, Zehner, Hunderter,… in die erste Zeile. So kann man die Zahl 1032 eintragen:
Stellenwertsymbol | T | H | Z | E | ||
|---|---|---|---|---|---|---|
Stellenwert | ||||||
1 | 0 | 3 | 2 |
Wenn man Nachkommastellen eintragen möchte, ergänzt man z,h,t,… für Zehntel, Hundertstel, Tausendstel,…
Stellenwert-symbol | H | Z | E | , | z | h | ||
|---|---|---|---|---|---|---|---|---|
Stellenwert | , | |||||||
1 | 3 | 2 | , | 3 | 5 |
Zwischen Stellenwertsystemen wechseln
Man kann Zahlen in verschiedenen Stellenwertsystemen darstellen.
Beispiele:
Stelle die Zahl 31 zur Basis 5 dar!
Man kann sich 31 Punkte vorstellen, die geordnet werden und die man jetzt zu fünft bündeln möchte.
Wie viele Fünferbündel erhält man?
Rechne .
6 Fünferbündel und 1 einzelner Punkt.
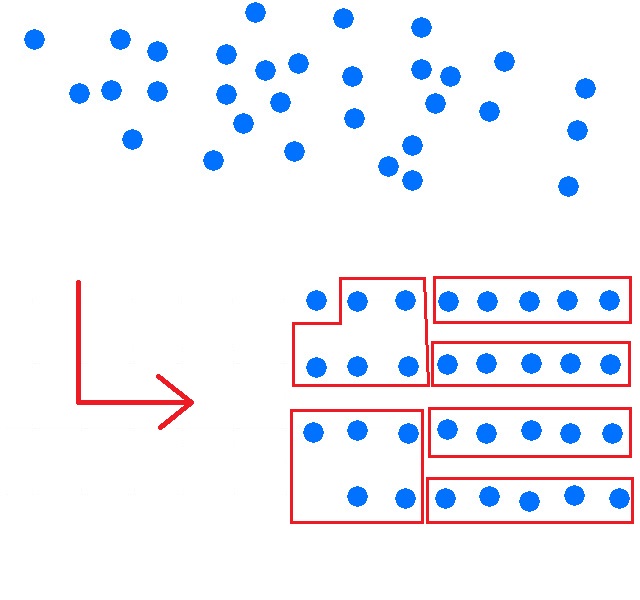
Die sechs Bündel muss man nun wieder zu fünft bündeln, da es die Ziffer 6 im Fünfersystem nicht gibt.
Rechne .
1 Fünferbündel-Bündel und 1 einzelnes Fünferbündel.
Ergibt insgesamt:
1 orangefarbenes Bündel, 1 rotes Bündel, 1 Punkt.
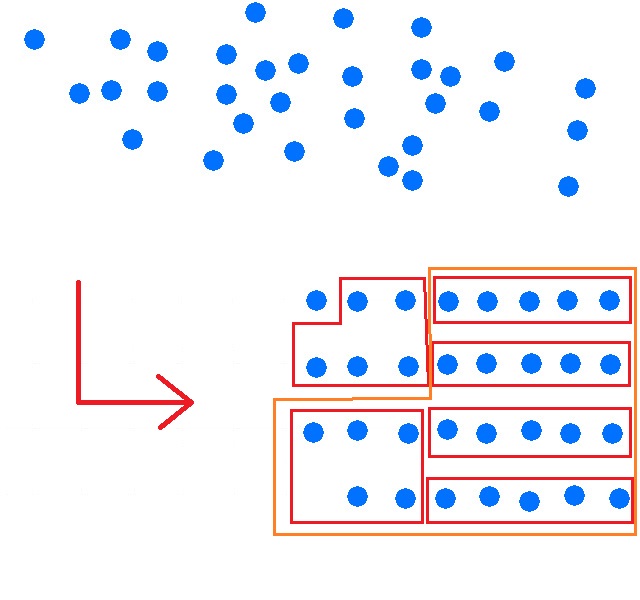
Stelle die Zahl zur Basis 4 dar!
Beschreibung | Rechnung |
|---|---|
Schreibe als Summe und berechne: | |
Teile 306 durch 4: | |
Teile 76 durch 4: | |
Teile 19 durch 4: | |
Teile 4 durch 4: | |
Teile 1 durch 4: | |
Weil das Ergebnis der Division 0 ist, ist man hier fertig. Die Reste sind nun jeweils die Vorfaktoren der Stellenwerte. Der erste Rest, den wir berechnet haben, gehört zum Stellenwert , der zweite zu usw. |
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
