Skizziere das Dreieck für $\alpha =50\mathrm{°}\backslash alpha\; =\; 50°$.

Du sollst ein Dreieck $\mathrm{\Delta }A{B}_{1}C\backslash Delta\; AB\_1C$ zeichnen, wobei die Strecke $\overline{AC}\backslash overline\{AC\}$ $4\text{cm}4\backslash ;\backslash text\{cm\}$ lang und der Winkel $\mathrm{\measuredangle }{B}_{1}AC=\alpha =50\mathrm{°}\backslash measuredangle\; B\_1AC=\backslash alpha=50°$und der Winkel $\mathrm{\measuredangle }AC{B}_1=2\alpha =2\cdot {50}^{\circ }=100\mathrm{°}\backslash measuredangle\; ACB\_1=2\backslash alpha=2\backslash cdot50^\{\backslash circ\}=100°$groß sind. Das folgende Applet zeigt dir, wie du das machen kannst.

Finde eine Formel für $\overline{B_{n}C}\backslash overline\{B\_nC\}$ .

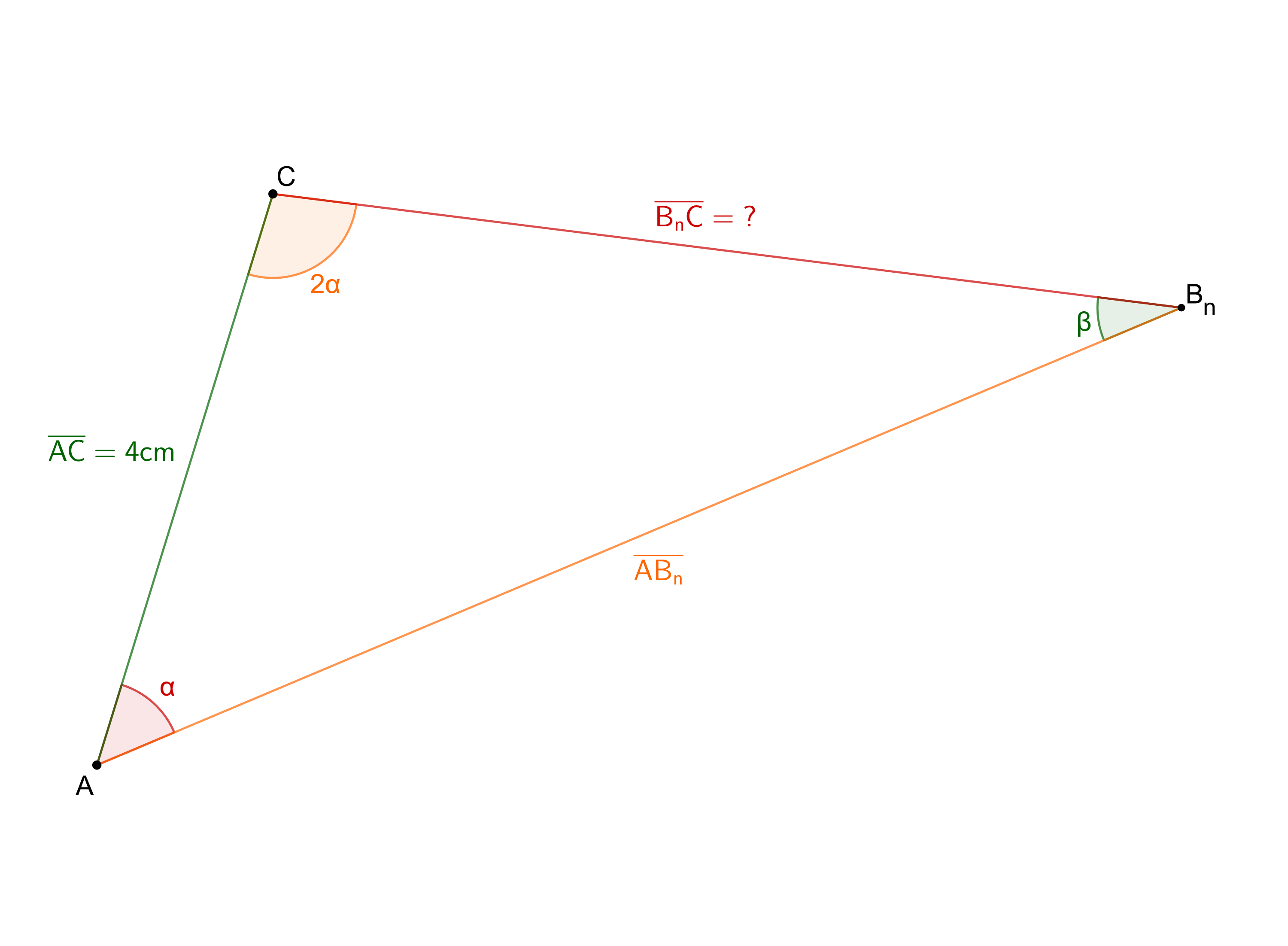
Um eine Formel für die Länge der Strecke $\overline{B_{n}C}\backslash overline\{B\_nC\}$ zu finden, schau dir zunächst das Dreieck an, wie du es bisher kennst:

Du kennst die Strecke $\overline{AC}\backslash overline\{AC\}$ und sollst den Winkel $\alpha \backslash alpha$ für die Lösung verwenden. Weil das Dreieck nicht rechtwinklig ist, kommt nur der Sinussatz in Frage.

Der Sinussatz sagt, dass das Verhältnis des Sinus jeden Winkels und der Länge der gegenüberliegenden Strecke gleich ist:

Zwei der Winkel sind mit $\alpha \backslash alpha$ und $2\alpha 2\backslash alpha$ gegeben, $\beta \backslash beta$ ergibt sich nach der Winkelsumme im Dreieck von ${180}^{\circ }180^\backslash circ$ zu

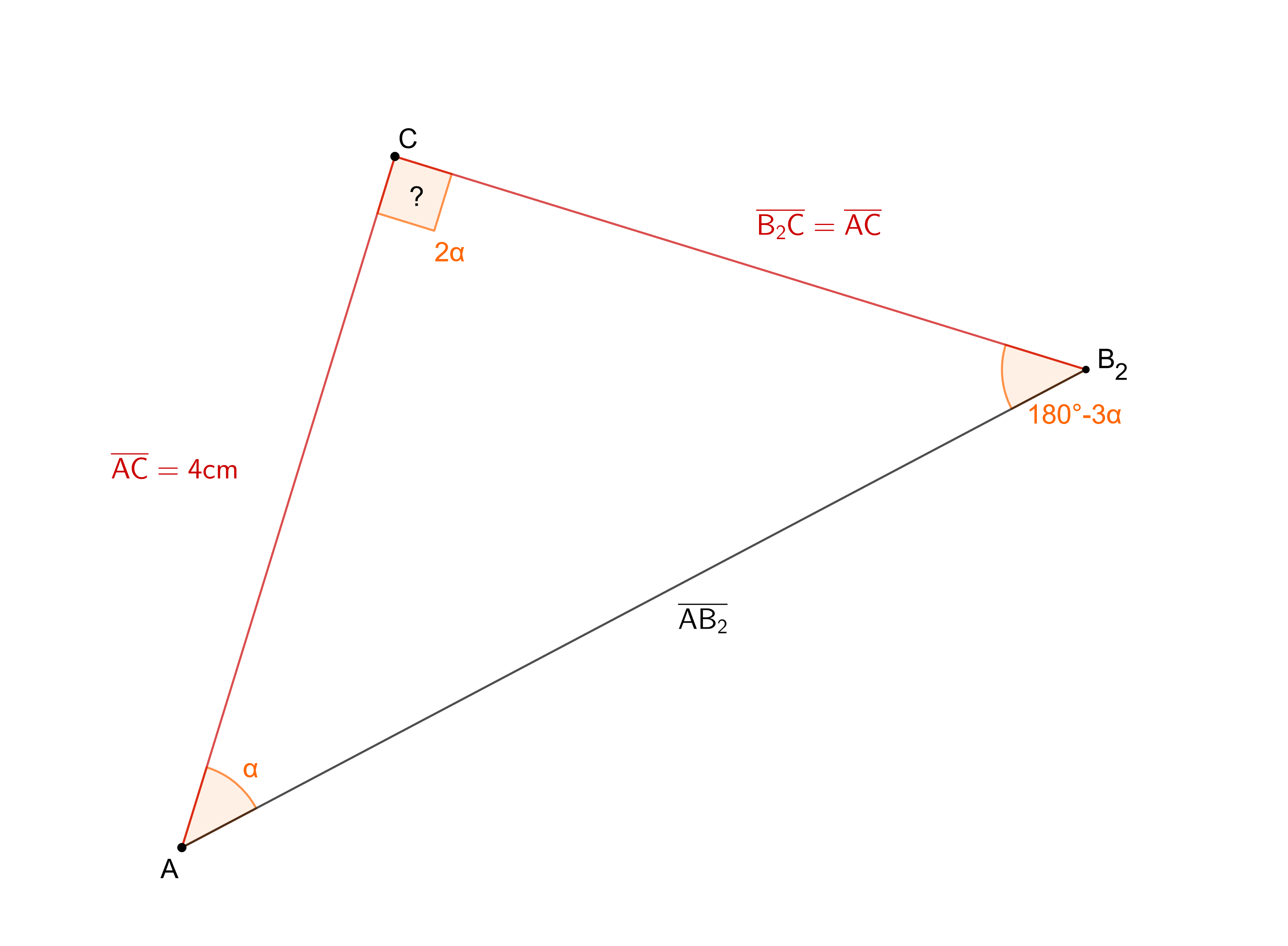
Die Winkel kannst du in deiner Lösung alle verwenden. Der dritte Term interessiert nicht, weil $\overline{A{B}_n}\backslash overline\{AB\_n\}$ weder gesucht, noch gegeben ist. Du kannst die Formel nach $\overline{B_{n}C}\backslash overline\{B\_nC\}$ umstellen:

Nun kannst du, wie in der Aufgabenstellung verlangt, eine Supplementbeziehung für den Sinus anwenden:

und erhältst damit

Zeige, dass das Dreieck, wenn es gleichschenklig ist, auch rechtwinklig ist.

In einem gleichschenkligen Dreieck sind zwei Innenwinkel gleich, nämlich die Winkel zwischen den Schenkeln und der Basis:

In diesem Dreieck bedeutet das dann, dass

gelten muss. Die Formel kannst du umstellen: Addiere zunächst $3\alpha 3\backslash alpha$ auf beiden Seiten.

und teile dann durch 4:

Nun hast du herausgefunden, dass der Winkel $\alpha {45}^{\circ }\backslash alpha\; \backslash ;45^\backslash circ$ groß sein muss, wenn das Dreieck rechtwinklig ist. Es ist in der Aufgabenstellung gegeben, dass $\mathrm{\measuredangle }AC{B}_n=2\alpha =2\cdot {45}^{\circ }={90}^{\circ }\backslash measuredangle\; ACB\_n=2\backslash alpha=2\backslash cdot45^\backslash circ=90^\backslash circ$ ist, also ist das Dreieck tatsächlich rechtwinklig!