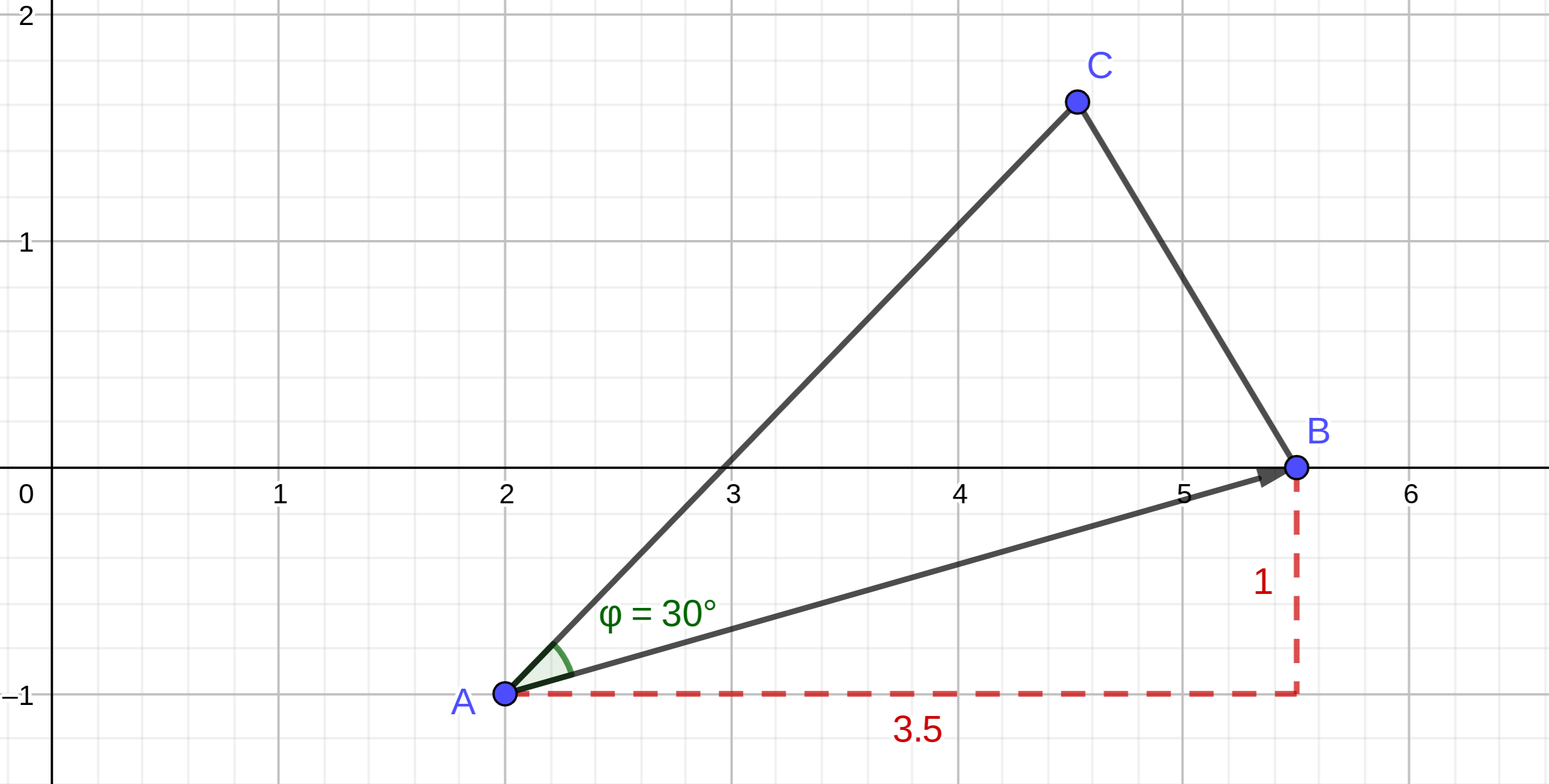
Der Punkt legt zusammen mit den Pfeilen
und Punkten gleichschenklige Dreiecke mit den Basen fest
. Es gilt: .
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
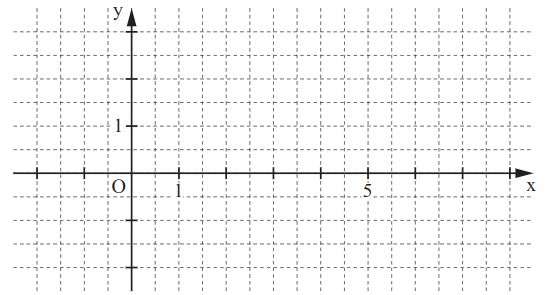
Berechnen Sie die Koordinaten des Pfeils für und zeichnen Sie das zugehörige Dreieck in das Koordinatensystem zur Aufgabenstellung ein.
Bestimmen Sie rechnerisch die Koordinaten der Punkte in Abhängigkeit von .
[Ergebnis:
Für welches Maß von wird die Abszisse der Punkte minimal? Kreuzen Sie an.
Für gibt es das Dreieck , dessen Punkt auf der -Achse liegt. Berechnen Sie die Koordinaten des Punktes .